单词

  1. cascade：     级联
  2. telepresence：“网真”
  3. occlusions：  遮挡
  4. anatomical：  解剖
  5. amenable：    有义务的
  6. skeletal：    骨骼的
  7. kinematic：   运动
  8. egocentric：  以自我为中心
  9. monocular：   单眼的
  10. robust：      健壮的
  11. Methodology： 方法
  12. vertices：    顶点
  13. ablation:     消融
  14. Metrics：     指标

小小科普

参考： 图卷积神经网络

图卷积神经网络：

  • 简单的来说就是其研究的对象是图数据（Graph），研究的模型是卷积神经网络；

    Euclidean data：

  • Euclidean data最显著的特征就是有规则的空间结构，比如图片是规则的正方形栅格，比如语音是规则的一维序列。而这些数据结构能够用一维、二维的矩阵表示，卷积神经网络处理起来很高效；

    Non Euclidean data：

  • 推荐系统、电子交易、计算几何、脑信号、分子结构等抽象出的图谱；

    作者的一些思考

    难点

  • 手或者目标对象的遮挡问题；

  • 第一人称相机拍摄过程中引入极大的相机的抖动；

    如何实现估计

  • 对手和物体进行整体把握，不宜分别估计；

    • 手和物体在交互过程中是有相互制约的；
    • 对手姿态的估计，同样可以为物体的属性提供线索；
    • 物体的姿态同样限制握住它的手的姿态；
  • 在估计过程时，将手以及物体表征为一个单独的图；
  • 产生3D姿态估计是，结合第一人称和第三人称视频数据（？？？）；
    • 首先估计2D关键点和物体边界；
    • 然后在二维姿态估计的基础上，分层次联合恢复深度信息（3D）；
    • 基于检测的模型在检测2D关键点方面效果非常好，但是由于三维检测时的高度非线性以及巨大的输出空间，使得基于回归的模型在三维检测方面更流行；

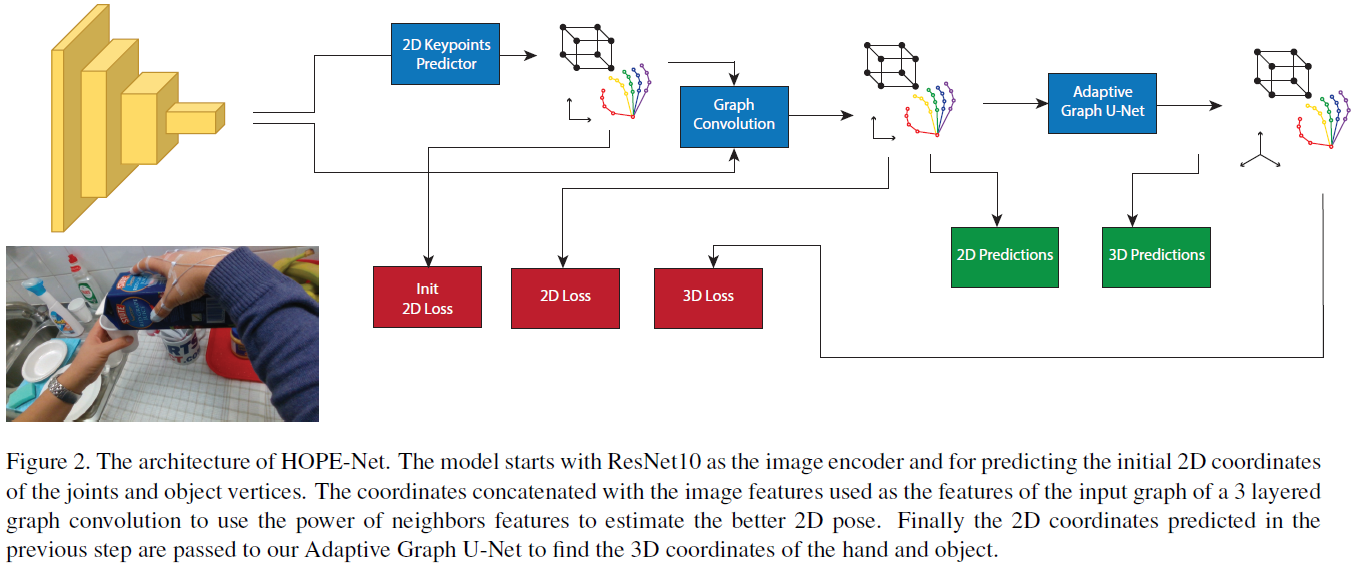
  • 模型分两步走：

    • 首先是2D关键点以及物体边界估计；
    • 然后是2D到3D的转换，改进Adaptive Graph U-Net实现；
    • 这两步可以分开进行训练，2D到3D转换网络使用了大量合成数据（一个数据集）进行训练；

      方法分析

      image.png

      步骤

      从上图可以看出来，模型至少经过了三步：初步估计2D关键点，2D关键点提纯，2D转3D；
      初步估计2D关键点

  • 采用ResNet10提取特征，并估计初始的2D关键点；

2D关键点提纯

  • 将坐标与图像特征连接起来作为3层图卷积的输入图的特征，利用邻域特征的力量来估计更好的二维位姿；

2D转3D

  • Adaptive Graph U-Net；

    图像编码与图卷积

  • 采用轻量级ResNet（ResNet10）作为图像编码器，其为每张图片输出2048D的特征向量，然后采用一个全连接层产生初始的2D关键点数据；（回归出2D关键点）

  • 将2048D的Image feature和每个关键点坐标进行连接产生多个2050D的特征，这些特征将被用于产生节点；
  • 利用3层结构的自适应图卷积网络，结合临近信息对2D关键点进行修改；

  • 最后将修改后的关键点输入到自适应U-Net中实现维度的转换；

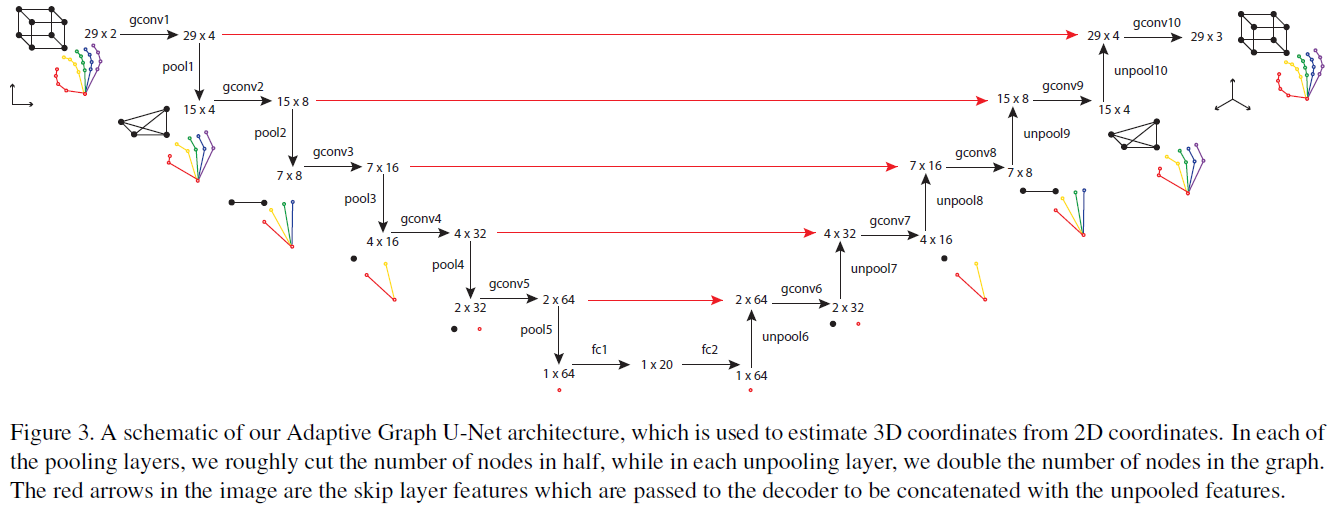
    Adaptive Graph U-Net

    原版的U-Net尚未了解…
    将问题转为图问题的原因：

  • 能够利用临近信息；

  • 更能够发现手和物体的关系；

image.png

图卷积

之前了解过Graph U-Net，但是其中的gPool和gUnpool在此处不再实用，因为此处的graph为稀疏图，采用该论文中的gPool，基本上会导致节点的孤立。

图卷积操作

此映射的作用是：将临接节点的信息不断汇总到本节点。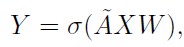
image.png
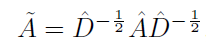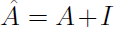其中：image.png，image.png，HOPE-Net: A Graph-based Model for Hand-Object Pose Estimation_2020CVPR - 图6
此公式和卷积运算的关系可以参考GCN论文！（卷积运算可以最终近似推出此公式）
其中一个任务就是确定临接矩阵，当然可以选择普通的，按照关键点实际连接情况进行临接矩阵的确定。但是，通过实验发现，让网络自行学习临接矩阵更优（此类操作严格来说使得该矩阵不再是临接矩阵）。所以Adaptive graph convolution需要更新HOPE-Net: A Graph-based Model for Hand-Object Pose Estimation_2020CVPR - 图7

运算实现代码

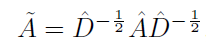image.png实现

  1. # A_hat is trainable
  2. A_hat = Parameter(torch.eye(29).float().cuda(), requires_grad=True)
  3. # ......
  4. # A_hat: batch * 29 * 29
  5. batch, N = A_hat.shape[:2]
  6. # D_hat: batch * 29
  7. D_hat = (torch.sum(A_hat, 1) + 1e-5) ** (-0.5)
  8. L = D_hat.view(batch, N, 1) * A_hat * D_hat.view(batch, 1, N)
  9. # 此处的矩阵运算与数学意义上的不同，但是显然和上式公式是等价的。但是相对于矩阵乘法来说降低了运算量

HOPE-Net: A Graph-based Model for Hand-Object Pose Estimation_2020CVPR - 图9卷积运算实现

  1. def forward(self, X, A):
  2.     batch = X.size(0)
  3.     #A = self.laplacian(A)
  4.     # A_hat: batch * 29 * 29
  5.     A_hat = A.unsqueeze(0).repeat(batch, 1, 1)
  6.     X = self.fc(torch.bmm(self.laplacian_batch(A_hat), X))
  7.     if self.activation is not None:
  8.         X = self.activation(X)
  9.     return X

注：nn.Linear函数好像和之前印象中的存在偏差！（不需要进行“拉直”操作）
(之前理解的Linear不对）
gPool和gUnpool实现

  1. class GraphPool(nn.Module):
  3.     def __init__(self, in_nodes, out_nodes):
  4.         super(GraphPool, self).__init__()
  5.         self.fc = nn.Linear(in_features=in_nodes, out_features=out_nodes)
  8.     def forward(self, X):
  9.         # 是对节点数进行pool，所以需要transpose
  10.         X = X.transpose(1, 2)
  11.         X = self.fc(X)
  12.         X = X.transpose(1, 2)
  13.         return X

Graph U-Net实现

  • 就是先不断地利用conv和pool不断降低节点数和feature大小；
  • 然后利用conv和unpool不断增加节点数和feature的大小；

  • 显然由于这是矩阵运算，所以对于feature输出size的控制相对于图片卷积来说方便很多；

    1. class GraphUNet(nn.Module):
    3.   def __init__(self, in_features=2, out_features=3):
    4.       super(GraphUNet, self).__init__()
    6.       self.A_0 = Parameter(torch.eye(29).float().to(device), requires_grad=True)
    7.       self.A_1 = Parameter(torch.eye(15).float().to(device), requires_grad=True)
    8.       self.A_2 = Parameter(torch.eye(7).float().to(device), requires_grad=True)
    9.       self.A_3 = Parameter(torch.eye(4).float().to(device), requires_grad=True)
    10.       self.A_4 = Parameter(torch.eye(2).float().to(device), requires_grad=True)
    11.       self.A_5 = Parameter(torch.eye(1).float().to(device), requires_grad=True)
    13.       self.gconv1 = GraphConv(in_features, 4)  # 29 = 21 H + 8 O
    14.       self.pool1 = GraphPool(29, 15)
    16.       self.gconv2 = GraphConv(4, 8)  # 15 = 11 H + 4 O
    17.       self.pool2 = GraphPool(15, 7)
    19.       self.gconv3 = GraphConv(8, 16)  # 7 = 5 H + 2 O
    20.       self.pool3 = GraphPool(7, 4)
    22.       self.gconv4 = GraphConv(16, 32)  # 4 = 3 H + 1 O
    23.       self.pool4 = GraphPool(4, 2)
    25.       self.gconv5 = GraphConv(32, 64)  # 2 = 1 H + 1 O
    26.       self.pool5 = GraphPool(2, 1)
    28.       self.fc1 = nn.Linear(64, 20)
    30.       self.fc2 = nn.Linear(20, 64)
    32.       self.unpool6 = GraphUnpool(1, 2)
    33.       self.gconv6 = GraphConv(128, 32)
    35.       self.unpool7 = GraphUnpool(2, 4)
    36.       self.gconv7 = GraphConv(64, 16)
    38.       self.unpool8 = GraphUnpool(4, 7)
    39.       self.gconv8 = GraphConv(32, 8)
    41.       self.unpool9 = GraphUnpool(7, 15)
    42.       self.gconv9 = GraphConv(16, 4)
    44.       self.unpool10 = GraphUnpool(15, 29)
    45.       self.gconv10 = GraphConv(8, out_features, activation=None)
    47.       self.ReLU = nn.ReLU()
    49.   def _get_decoder_input(self, X_e, X_d):
    50.       return torch.cat((X_e, X_d), 2)
    52.   def forward(self, X):
    53.       # X: batch * 29 * 2
    54.       X_0 = self.gconv1(X, self.A_0)
    55.       X_1 = self.pool1(X_0)
    57.       X_1 = self.gconv2(X_1, self.A_1)
    58.       X_2 = self.pool2(X_1)
    60.       X_2 = self.gconv3(X_2, self.A_2)
    61.       X_3 = self.pool3(X_2)
    63.       X_3 = self.gconv4(X_3, self.A_3)
    64.       X_4 = self.pool4(X_3)
    66.       X_4 = self.gconv5(X_4, self.A_4)
    67.       # X_5: batch * 1 * 64
    68.       X_5 = self.pool5(X_4)
    70.       global_features = self.ReLU(self.fc1(X_5))
    71.       global_features = self.ReLU(self.fc2(global_features))
    73.       X_6 = self.unpool6(global_features)
    74.       X_6 = self.gconv6(self._get_decoder_input(X_4, X_6), self.A_4)
    76.       X_7 = self.unpool7(X_6)
    77.       X_7 = self.gconv7(self._get_decoder_input(X_3, X_7), self.A_3)
    79.       X_8 = self.unpool8(X_7)
    80.       X_8 = self.gconv8(self._get_decoder_input(X_2, X_8), self.A_2)
    82.       X_9 = self.unpool9(X_8)
    83.       X_9 = self.gconv9(self._get_decoder_input(X_1, X_9), self.A_1)
    85.       X_10 = self.unpool10(X_9)
    86.       X_10 = self.gconv10(self._get_decoder_input(X_0, X_10), self.A_0)
    88.       return X_10

    Graph Pooling

    采用全连接层，并将其作用于feature matrix的transpose；
    特点：

  • 全连接层kernel综合所有特征；

  • 输出想要个数的节点数；

    Graph Unpooling

    同样采用全连接层，于Pooling操作类似，同样作用于feature matrix的transpose产生预期数量的节点数，最好再将其transpose回来。

    Loss Function

    loss由三部分组成：
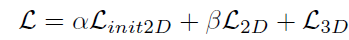
    image.png
    分别是：初始的2D loss，提纯的2D loss以及3D loss。
    loss计算时采用Mean Squared Error

    1. outputs2d_init, outputs2d, outputs3d = model(inputs)
    2. loss2d_init = criterion(outputs2d_init, labels2d)
    3. loss2d = criterion(outputs2d, labels2d)
    4. loss3d = criterion(outputs3d, labels3d)
    5. loss = (lambda_1)*loss2d_init + (lambda_1)*loss2d + (lambda_2)*loss3d

    实现细节

    模型训练

  • 针对不同步骤的模型进行分开训练；

  • 数据增强的方式提高模型的健壮性；