Deconvolution_2011ICCV

论文地址 Adaptive deconvolutional networks for mid and high level feature learning

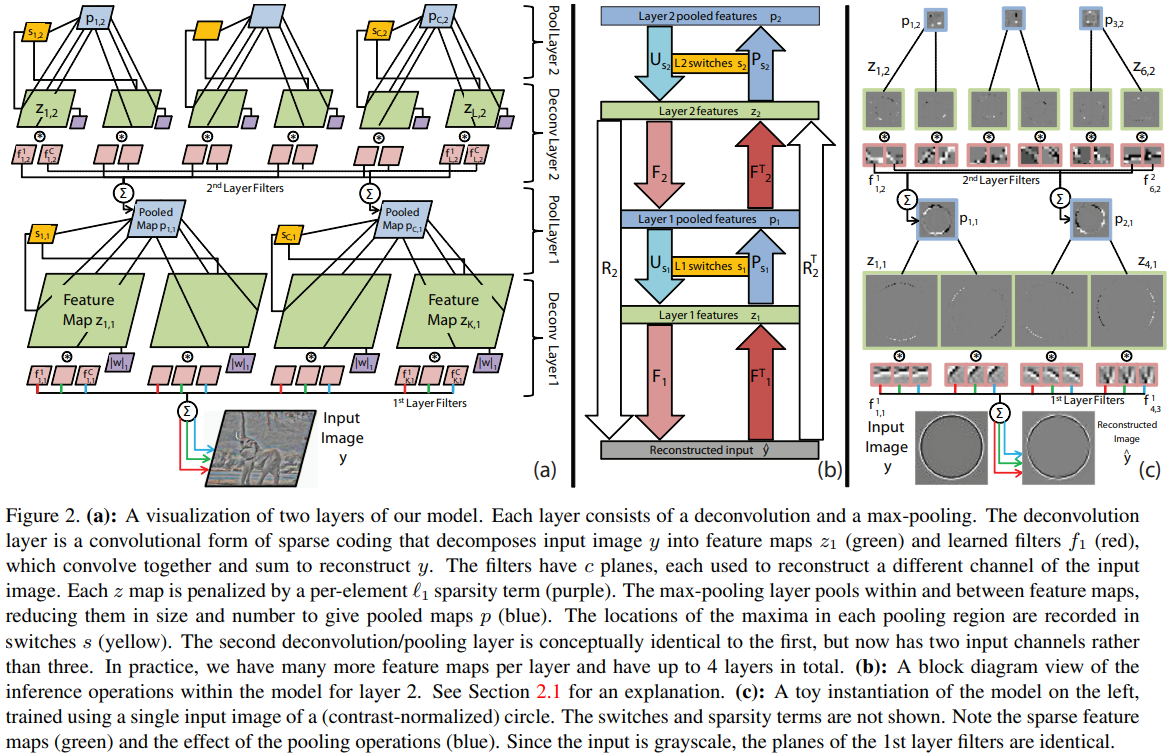
本文为解决两个问题提供了解决方案，第一个和不变性相关，第二个和层次模型中采用的逐层训练方案有关。本文对这两个问题的解决方案是：通过对每张图像的计算，引入一组潜在的开关变量，使模型的过滤器局部适应观察数据。
这些开关还提供了一个直接到输入的路径，甚至可以从模型的高层输入，这使得每一层都可以根据图像进行训练，而不是根据前一层的输出。

逐层训练往往比较脆弱，并且对于层数太多的模型不切实际。 由于缺乏有效训练各层输入的方法，这些模型被贪婪地自底向上训练，使用前一层的输出作为下一层的输入。（往往高层输入和输入图像关联越来越小）一个比较简单的想法：先整体训练，然后再从最后一层开始，每层以上一层的输出为输入进行该层的训练，训练一层则固定一层，依次递推到网络第一层，然后再循环上面的方式进行训练，直到达到预期目标。

方法

本文模型生成了一个过度完整的图像表示，它可以用作标准对象分类器的输入。该模型使用卷积稀疏编码(deconvolution)和最大值池化的多层交替层分层分解图像。每个反卷积层都试图在一个超完备的特征图集合上的稀疏约束下，直接最小化输入图像的重构误差。

损失函数

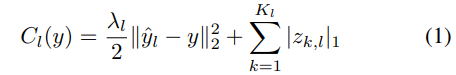
其中，表示网络第层，表示原输入图像，表示重构图像，表示的是feature map，控制比列。

希望feature map能够足够稀疏！（为何？） 损失函数以输入为标准，希望最小化重构图像误差。

Deconvolution:

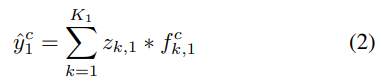
上述公式是网络第一层重构输入图像的公式，其中表示channel，表示的是第一层的第个feature map，表示的是第一层的第个filter的第个通道。

如果将卷积核加法组合成一个卷积矩阵，将多个2D的feature maps组合成一个单独的向量，从而将公式(2)转为公式(3)：

这是将第一层的所有利用来重构，其也可以表示为单个重构之后叠加的形式： ，其中的表示第个或者其对应的矩阵上标。

Pooling

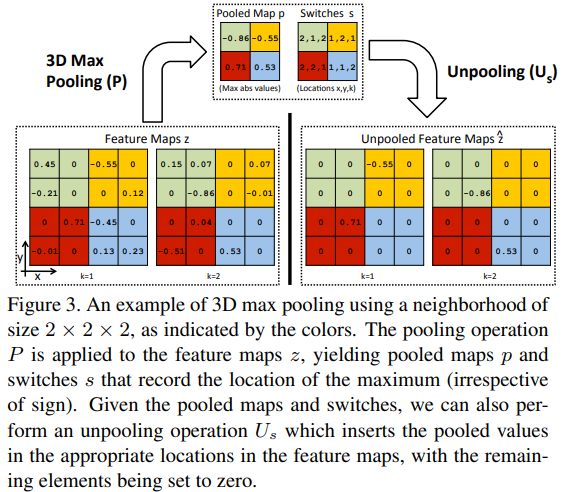
如上图所示，在进行最大值池化的时候，我们将产生两个map，一个是池化后的map ，它记录了最大值，另一个是记录了最大值得坐标，由于是，图中最大值坐标是3元组（第一个表示，第二三个表示的卷积核坐标下的）。其可以表示为：，其中的是一个由所产生的二值选择矩阵。
在过程中，非最大值处进行补0操作。其可以表示为：, 其中(当然, 这个不是显式等价的, 关键还要看如何实现Pooling操作)

如果池化过程是将feature map转为向量,那么易证上述表示是成立的!

对于多层网络不断堆叠, 其映射到输入像素空间可以表示为: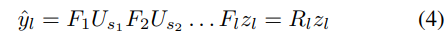

其中为定义的重构运算符. 与之对应的, 我们可以定义将输入像素空间映射到feature map的运算符:

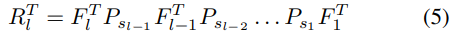
之前思考过, 为什么用转置来替代逆运算. 在上面可以看到3D Max Pooling操作完全是没有问题的, 并且卷积运算的话也可以保证运算的shape满足要求. 当然对于卷积操作来说, 其并不等价于逆运算. 模型的一个重要属性是: 如果给定了, 那么和都是线性的.

我们最终的目的是找到这样的特征: 通过Deconvolution操作之后, 得到的和误差到达能够达到的最小值.

推理

采用ISTA算法, 交替进行gradient 和 shrinkage 步骤.

gradient step

对于来说, 其梯度为: , 根据此式可以知道如果需要计算梯度可以: 先利用重构, 然后得到偏差, 最后将偏差前向传播即得到

这个方法非常精妙!!!

最后对进行更新(居然对中间的feature map进行更新!):

Shrinkage step

在梯度计算之后, 我们利用Shrinkage 操作来使获得的稀疏化.（将中小元素置0）

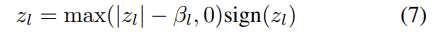
Pooling/unpooling

由于前面修改了, 所以需要修改池化操作的. 一旦推理收敛，将被固定，为训练上面的层做好准备。

值得注意的是, 本文网络结构中, 是先进行3D Max Pooling之后, 再进行反向去重构.

产生滤波器的输出很好理解，即是得到模型的参数。那么如何理解输出feature maps？这可以和前面的逐层训练相关联，产生这样的feature map可以用于解决逐层训练输入问题。 理解方式：本文的算法和通常的CNN理念差异比较大，传统的方法是训练模型之后，拿模型去对其它未被训练的数据做预测。本文的特点是通过学习学到，滤波器参数共享，其学习和通常的CNN学习比较相似，网络的前向传播和普通CNN的前向传播作用完全不同！

可以看到算法也是从低层开始逐步到高层进行训练的，滤波器为所有图像共享的参数。

全部学完之后才更新?!那么的话，好大呀！（是的，不同图片产生的当然不同罗）

Learning

学习的目的是，获取的估计值。对公式(1)进行求导并设置为0，由如下等式：

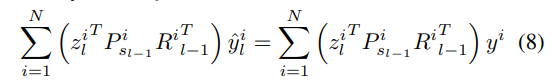
注意： 上面的操作也即是说希望找到使得误差关于具有极小值。

思考

基于上面的内容来看本文更类似一个传统的算法，而不是深度学习模型。本文通过对的不断学习来产生独特的，与通常的CNN差异很大。本文前向传播和重构过程的反向传播并不是逆运算，前向传播的作用仅仅在于计算一些梯度什么的。本文的方法是无监督的，对每个需要处理的图像都需要进行推理过程来产生对应的。值得一提的是，为了便于深层网络的学习，本文滤波器的参数学习和常规的CNN比较类似，倒是共享参数的。（的学习同时也是希望重构的输入和原输入误差更小）

修改的过程就是在找寻需要学习到的，这也是本文中最重要的东西； 根据开关变量每层训练结束之后的冻结可知，本文还存在一个假设：低层的特征通过前向传播产生高层的特征，模型反向进行时，即是它的一个逆运算（当然与之对应的前向传播不是本文模型的前向传播，此前向传播是一个隐式的前向传播），所以Max Pooling位置是对应的。

还有些没有看懂-_-!但是目前貌似理解了它的想法了！不应该用常规的CNN想法来理解这篇文章。

用于目标检测

正如前面所述，本文的模型最主要的功能是学习（其学习方式即执行前面讲的推理和学习），单单用这些特征图是无法进行目标检测的，还需要其它单元。本文采用的是和空间金字塔分类器（SPM）结合进行目标检测任务的实现。
其特征选取为：经过推理和学习之后，选取顶层最大激活的M个特征图，利用它们重构原图：，然后利用重构原图的第一层的特征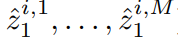输入SPM进行目标检测。