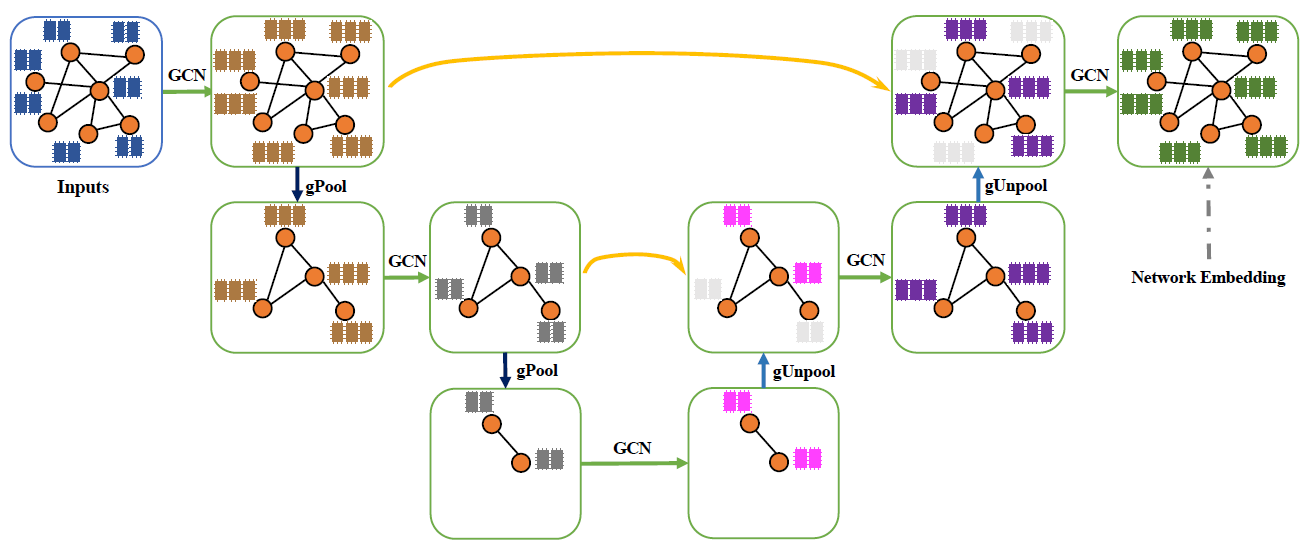
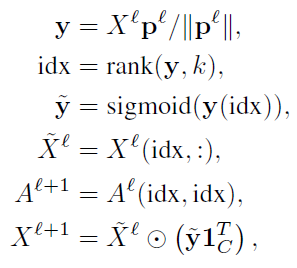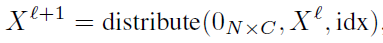原文链接:Graph U-Nets_2019 代码链接:https://github.com/HongyangGao/Graph-U-Nets
Graph U-Net应该是受到U-Net的启发
典型U-Net架构: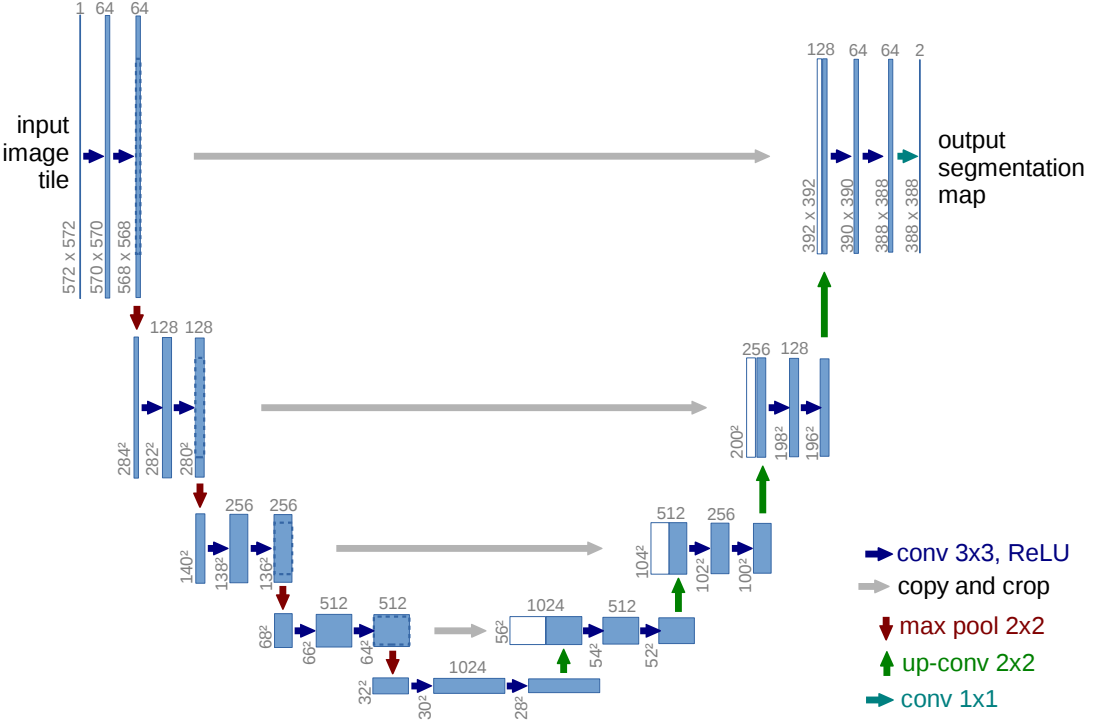
lattices:格子 consistently:始终如一地 aggregates:聚合
作者的一些思考
- CNN可以输入的数据是格状,他们可以看做特殊的图,所以图卷积网络相对于CNN来说是一种推广;
- 但是,对于普通的图数据,CNN难以处理,其原因包括在图数据处理时,池化和上采样不再自然;
- 为了解决这个问题,本文提出了Graph pooling(gPool)和Graph unpooling(gUnpool);
也就是说在GCN基础上进行进一步的延伸,引出 Pooling 操作。
针对gPool:
- 基于可训练投影向量中的标量投影值,自适应地选取部分节点去组成一个更小的图;
针对gUnpool:
- 是gPool的逆运算;
- 其利用对应gPool层中选择的节点位置信息将图形恢复到原始结构;
综合gPool和gUnpool设计Encoder和Decoder。
图卷积
希望模型能够学习节点表征。
用途:
- 节点分类;
- 连接预测;
先看GCN!要了解 Graph U-Net 需要先简单了解一下 GCN。
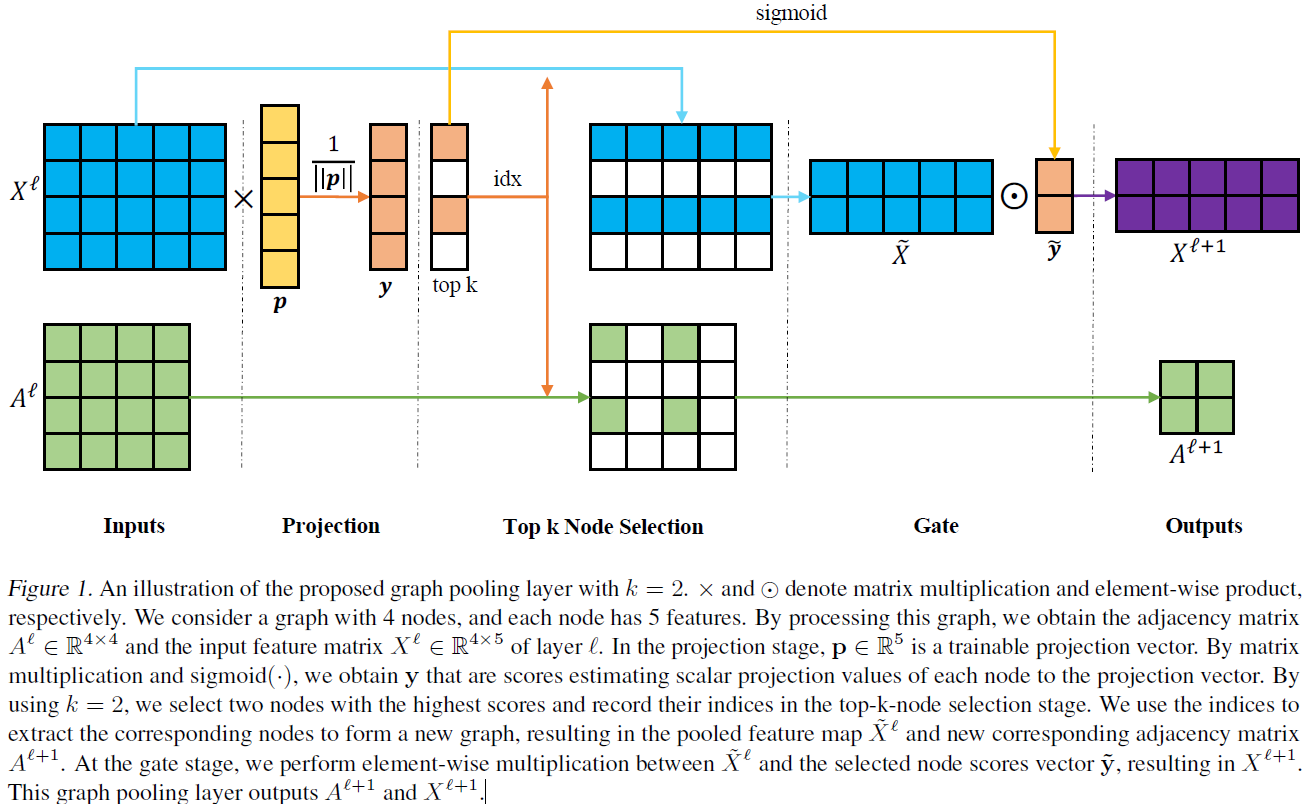
Graph Pooling Layer
Pooling想法
选取节点组成更小的图,从而实现pooling操作。
- 首先,引入可训练投影向量
,对于每个节点的特征,它将其投影为一个常数;
- 节点
的投影:
,显然其想法是将特征向量向指定方向进行投影,然后按照投影的大小进行筛选(有点PCA的味道);(PCA按照特征值大小进行维度筛选)
- 节点
为了使得
在反向传播中,可以被训练,需要进行 Gate 操作(如下图所示,就是一个对应位置元素相乘的操作)(如何看出可不可训练?)
首先构造
大小的0矩阵;
- 将
根据
信息放置到该矩阵中;
(可以看到gpool和gunpool存在对应关系,gunpool必须利用由gpool操作提供的信息,这也是为什么此网络为U-Net架构的原因吧!)
Graph U-Nets Architecture