基础概念回顾
图
端点以及对应的边组成的集合成为图,记作:
其中 V 表示的是端点,E 表示的是边。
临接矩阵
里面包含,图端点的临接关系。如果图中包括
个端点,那么临接矩阵
将是
矩阵。
无向图的临接矩阵:
注意对于无向图,主对角线为0(不讨论自己和自己的相邻)
度矩阵
某个端点的度表示的与之相连的边的数量,再细分又有入度和出度。
度矩阵是一个对角阵: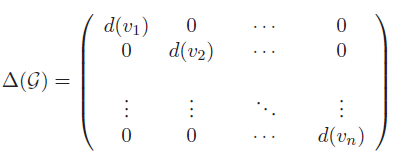
GCN网络
图表征
设图为,其特征如下:
- 每个端点
的特征有
维向量表示,端点个数为
,所以所以特征表示为
,其为
大小的矩阵;
- 其临接矩阵为
;
类比神经网络层,假设每层特征提取函数如下:;
GCN的目的就是希望,利用图的形式在特征之间构造连接,从而实现特征的组合。
一个简单的特征提取函数
其中:是非线性函数
其中
就是需要学习的参数,其 size 为
; 有了(2)现在我们的首要目的是确定
,即如何综合各个特征,从而引出图卷积。
如何理解
其中的其实就是将处于临接的特征进行求和产生新的特征,但是这样做的一个弊端是,求和前后数据在scale上产生较大差异,比较好的方法就是引入归一化,所以产生如下公式:
其中的表示的是度矩阵,可以看到这样就能够很好的实现平均操作;
值得一提的是:CNN的
卷积操作,同样可以看做是每个节点和临接节点的加权和!
实际特征提取函数
- 首先直接采用
会导致自身特征没有被引入,所以需要用
代替;
- 然后将
利用
代替(此时已并非平均之意),当然由于
已经被
替换,所以对应的
,其中
是
的度矩阵(相对于对角数据分别加1罗
)
从 GCN 理解 blog 中我们看到,在此公式之前,还有一系列相对较为复杂的图卷积形式。 激活函数的选取,可以是诸如Relu之类的。
图卷积示例
利用图卷积实现对车流量的预测
Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting
利用图结构对人体结构进行建模,并利用图卷积实现对人体动作的分类
Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition

