图像增强方法分为两大类:空间域方法和频域方法。
此处讨论的是灰度图。空间域处理定义如下:表示原图像,
表示处理后的图像。对图像的处理按照其依赖像素点个数可分为:点运算、局部运算和全局运算。此处的
通常是一个局部运算,即输出图像在指定坐标的像素值依赖于原图对应坐标处的一个领域(如下图所示)。
显然,上面的操作和CNN中的卷积操作是对应的。
最简单的情况,即单像素依赖,即上图中的矩形框为
,此时
成为灰度级变换函数,只是实现了一个强度的映射:
以下介绍经典的图像增强方法。并进行如下前提假设:
- 灰度级范围为
;
- 当图片中出现两图对比时:前图为原图,后图为增强图;
1 某些基本灰度变换
此处讨论单像素依赖的简单情况,这些方法都是按像素对原图像进行一定操作。包括三类基本函数:线性函数、对数函数和幂次函数,它们的效果如下图所示:
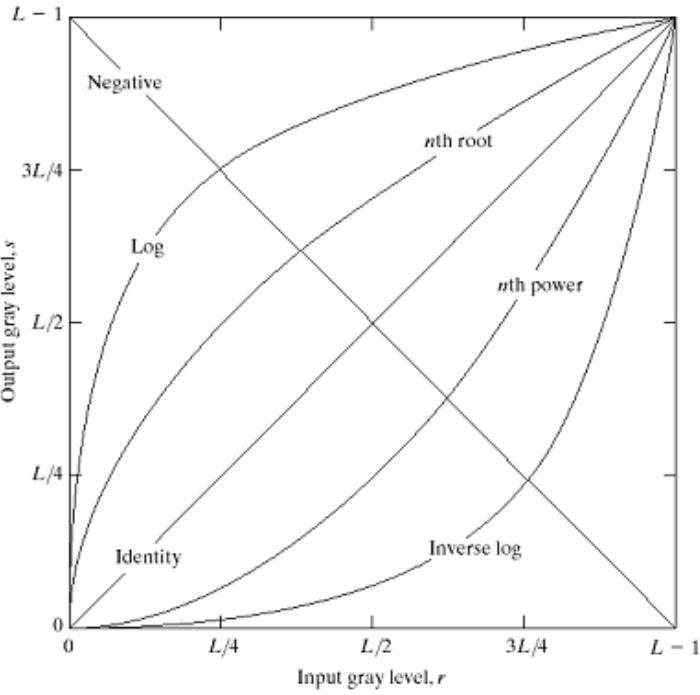
1.1 图像反转
如果灰度级范围为那么反转表达式:
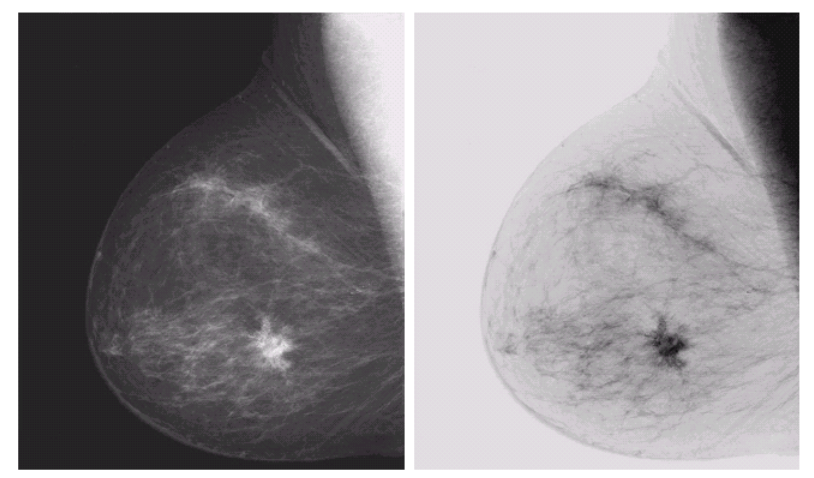
图像反转适用场合:增强嵌入与图像暗色区域的白色或灰色细节,特别是当黑色占主导地位。将暗色背景变为浅色,将白色或灰色细节变为深色,从而突出细节。
1.2 对数变换
对数变换表达式:
对数变换在数字信号处理中同样经常被用到,例如在绘制系统的幅频响应时。利用对数运算的原因:用于成像的信息动态范围非常大,这使得信息中的大值将成为重点,小值之间的差异难以分辨。所以对数变换适用场合:像素值具有非常大的动态范围。其效果:凸显暗背景下的细节信息。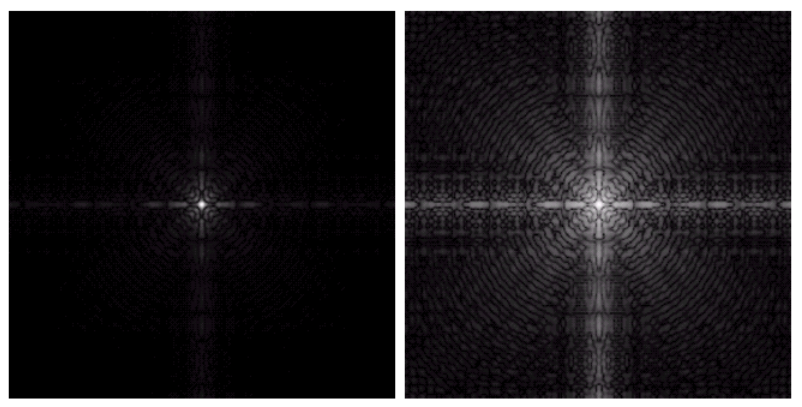
1.3 幂次变换
其表达式为:
根据选择的不同,幂次函数可以实现不同的效果。
,实现暗背景下的细节增强;
,实现亮背景下的细节增强;
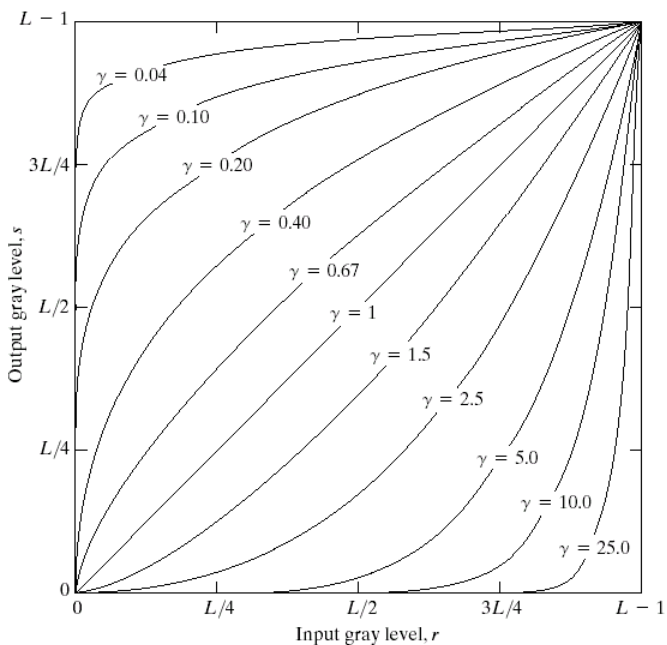
通常来说:图像获取、打印和显示的各种装置根据幂次规律产生相应(即原图和设备输出的图存在差异),在这种情况下需要进行伽马校正。
1.4 分段线性变换函数
分段线性变换函数优势在于形式可以任意合成,缺点在于需要更多的参数。
1.4.1 对比拉伸
对比拉伸,对不同像素范围的点进行不同的函数变换。对比拉伸的函数通常都是单调增加的,从而保持灰度级的次序。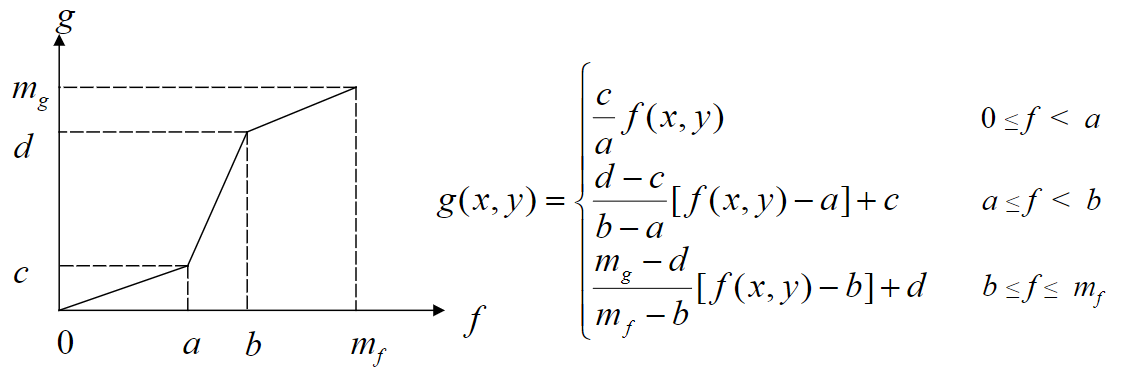
如下图的电子显微镜获取的花粉图像:(c为对比拉伸之后的结果,d为极端情况)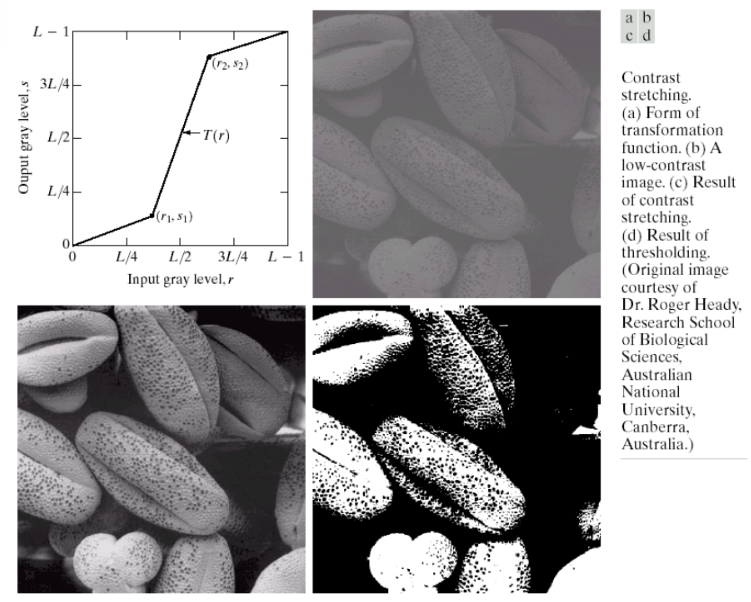
1.4.2 灰度切割
灰度切割是提高指定灰度范围的亮度,其应用包括:增强特征、增强X射线图中的缺陷。
下图展示了两种常用的灰度切割方式: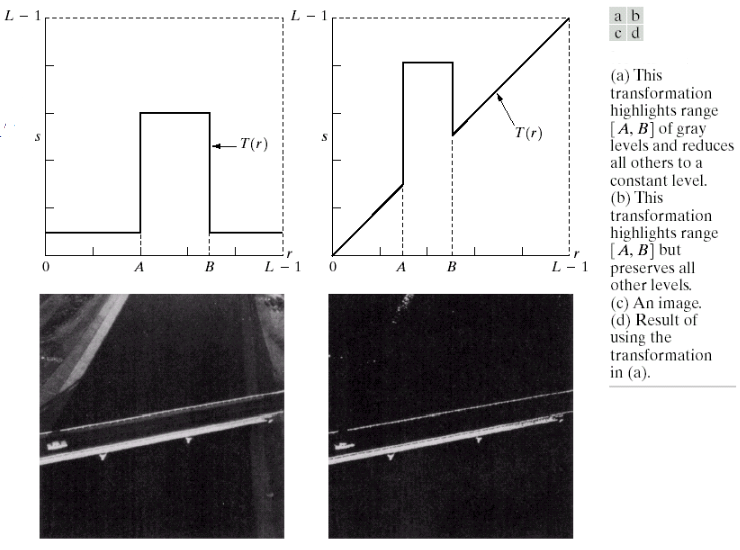
1.4.3 位图切割
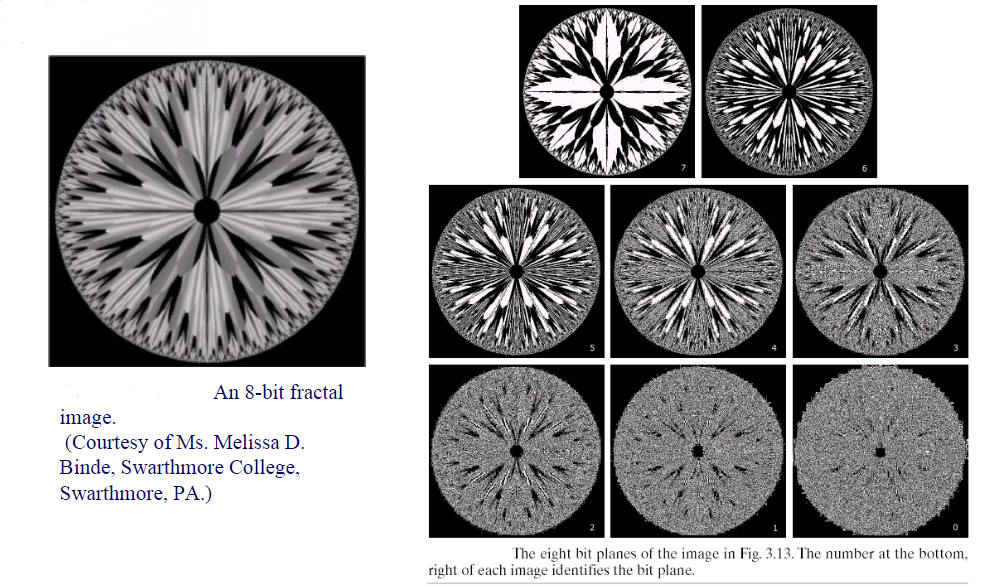
位图切割不从“图像像素值的整体”来进行变换,它针对灰度值的指定位进行变换从而实现图像增强。比如表示灰度值是采用,那么我们用每bit来生成一张二值化图像,从而可以产生8张二值化的图像。显然,最高阶的图像对原图影响是最大的;最低阶的影响最小,它们主要对图像中的一些微小细节有作用。
那么如何得到8张图像呢?
- 最高阶:
为0,
为1,即以127为阈值进行二值化;
- 次阶:原图像素值除2取整,得到新的图像,新的图像像素范围
,同样根据中间值63(除2取整)为阈值进行二值化;
- 以此类推……
2 直方图处理
直方图统计的是特定灰度级的像素个数,由于灰度级是离散的,所以直方图同样是离散的:,其中
表示第
级灰度,
表示该灰度的像素统计个数,归一化之后则得到比率:
。
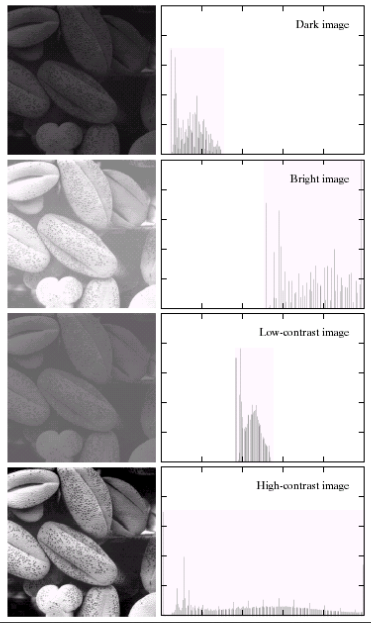
如上图所示,不同类型的图像其直方图分布有存在差异。例如暗图像,其直方图组成成分集中在灰度级低的一侧。直方图处理方法基于如下结论:若一幅图像的像素占有全部可能的灰度级并且分布均匀,则这样的图像有高对比度和多变的色调(这是我们希望的)。
2.1 直方图均衡化
连续公式推导
首先,考虑连续函数,其中的
是归一化的像素级,并且其连续变换,即
。
假设函数满足如下条件:
在区间
中为单值且单调递增;
- 当
时,
;
当然其反变换为
一张图像的连续灰度级可视为区间的随机变量,设
分别代表随机变量
的概率密度函数。(
表示不同的函数,这是符合实际情况的)
连续的可以用PDF,即随机密度函数,离散的则是采用归一化的比率,或者说归一化的概率。 在概率论中,对于随机变量概率分布的表征都是利用累积分布函数:
,其概率密度函数
,求取在
区间的概率:
以下推导两个成函数关系的随机变量的概率密度函数的关系:
设,
,
,并且他们的概率密度函数分别为为
和
,并假设函数
单调并且其逆变换
同样单调
由于:
利用概率密度函数表示则为:
两边对求导,则得到:
将此公式迁移到此处有:
现在我们选取特定的,其满足入校条件:
那么,将其带入(1.5.4)有:
显然此时输出图像在上均匀分布!
上面选取的
即是随机变量的概率分布定义式,其又被成为累积分布函数CDF。
离散情况
离散情况下,我们知道得就是一些离散灰度级的概率分布:
当然可以类似连续的操作,首先将梯度级归一化到,然后将上面的积分转为求和进行近似。
算法描述如下:
- 求出各个灰度级的直方图:
- 利用公式:
- 将
扩展到
,并进行量化操作即可
由于量化的原因使得,计算的不同的未被量化的之间差异较小的被合并,
差异小表征的是对应的概率小,所以换句话说,概率小的点将被合并从而产生更大概率,从而使得输出图像的概率分布更为均匀。
将像素值和概率相联系起来,谁能想得到?太强了!
2.2 直方图匹配
连续公式推导
直方图均衡事实上是直方图匹配的一个特殊情况,在直方图匹配中,我们希望输出规定的概率密度函数。
设为一随机变量,其满足:
再设同样为一随机变量,其满足:
也就是希望在原图和目标图中间,利用作为桥接(因为
是均匀分布,并且根据上面的推导知道,任意的分布经过CDF之后都是得到
):
所以:
离散情况
同样是积分变为求和:
所以:
其过程如下所示:(当然存在多个值对应一个
的情况,此处暂不讨论)
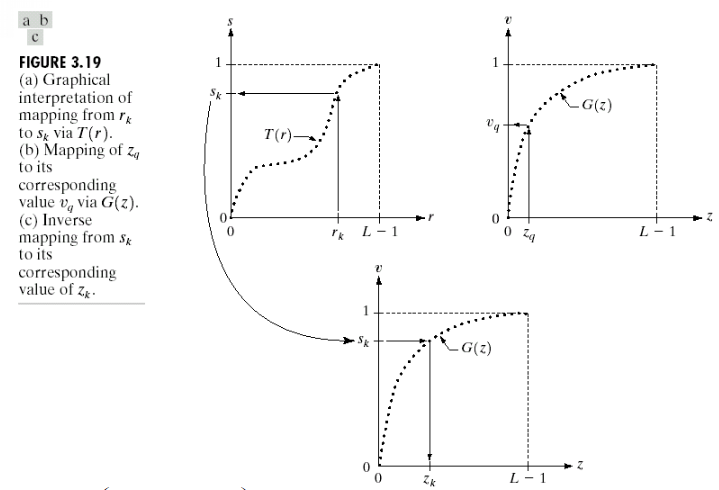
上面的过程类似于是一个查表的过程。
2.3 局部增强
3 用算术/逻辑操作增强
4 空间滤波基础
空间滤波和频域滤波存在对应的关系,但是存在差异。
滤波主要在领域上以及和领域同样大小的子图像上进行。子图像叫做滤波器(模板)等。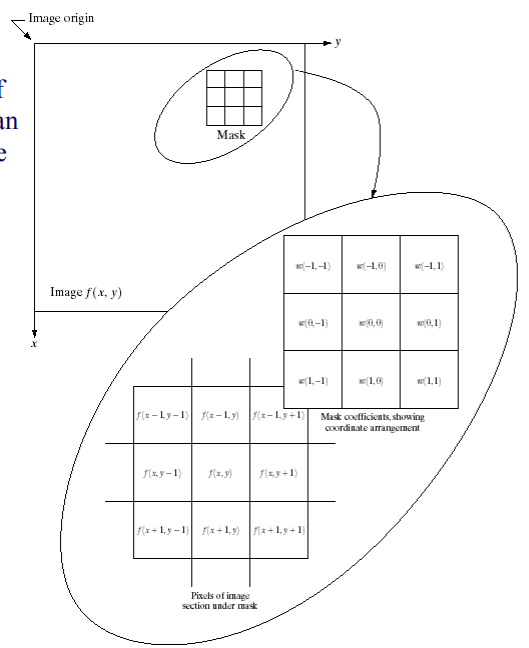
与卷积操作非常类似,滑动模板从而获取不同坐标的响应输出。为了对称,模板的大小一般取为奇数。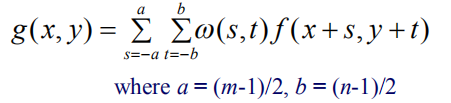
不考虑卷积操作的具体实现,公式简化为: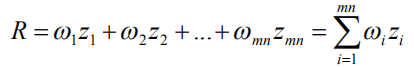
例如卷积操作:
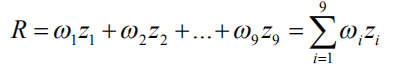
卷积操作,由于考虑图像的边界情况,不做任何操作则会出错:
- 限制卷积操作的范围;
- 边界运算只考虑部分像素;(相当于补零)
-
平滑空域滤波器
目标:通过对邻域操作,抑制图像中的噪声信号;模糊图像(平滑之后,图像会变模糊,从而去掉小的细节信息,连接中断线等)
平滑滤波器通过对领域像素取平均从而得到响应,所以又被称为低通滤波器或者平均值滤波器。
应用:噪声去除,模糊伪轮廓,消除图像中的不需要关注的细节信息;
平滑滤波器权值类型参考如下: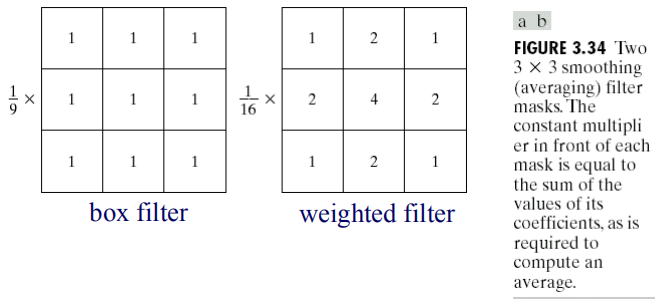
加权平滑滤波器:希望原位置处的像素对响应影响最大。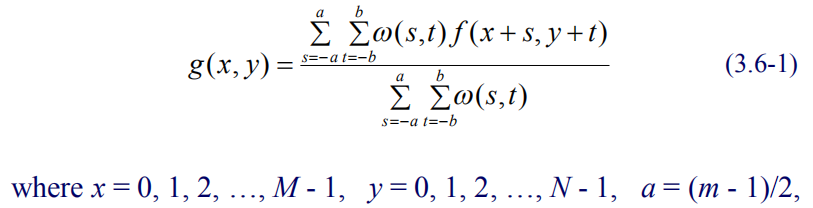
对比不同size kenel的平滑滤波器:
当细节的size小于等于kernel size时将被明显模糊化。
通过模糊操作进行感兴趣目标的提取(首先要根据目标的size确定kernel size):
其他平均手段
其它的平均化方法通常是非线性的,其希望保留边界信息。
被限制的数据平均操作;
- 逆梯度;
-
Kuwahara filter
Order-Statistics filter
对领域灰度值进行统计排序,然后选取特定位置的灰度值作为响应。典型:中值滤波器,选取排序过程中中间部分的灰度值作为输出。
中值滤波器:可以抑制椒盐噪声(噪声要么为0,要么为255,也被叫做脉冲噪声)中值滤波器
窗口内像素排序,选择中间像素值。

中值滤波器变体:百分比滤波器,选取的是某个占取特定百分比的像素值作为输出。(百分比是亮度的百分比,例如窗内亮度最低则记为0%,最高100%)
窗的大小要大于脉冲的2倍(貌似是2倍,未细究)宽度。锐化空间滤波器
平滑滤波器采用的求和—积分;
锐化滤波器与之相反—微分,从而提取差异,获取细节或边界信息。
导数算子与相邻像素的不连续性成正比。所以其对边界,噪声等突变有增强作用,对平滑区域有抑制作用。导数算子
离散一阶导数定义:
离散二阶导: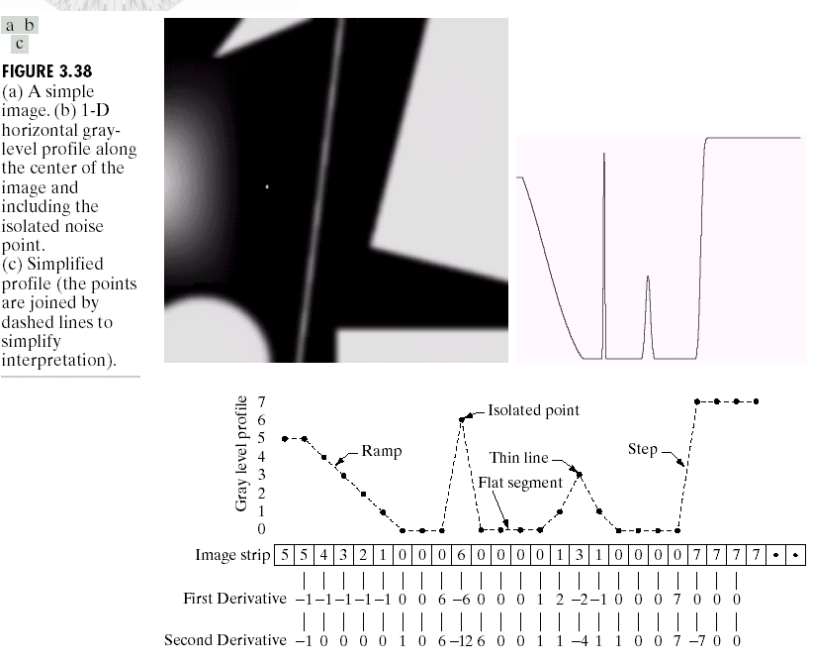
一阶导数将会扩充边界宽带,二阶导数对精细细节有更大的响应;一阶导数对灰度阶跃有比较高的响应,二阶导数对灰度变换的地方会产生双向响应值。拉普拉斯算子
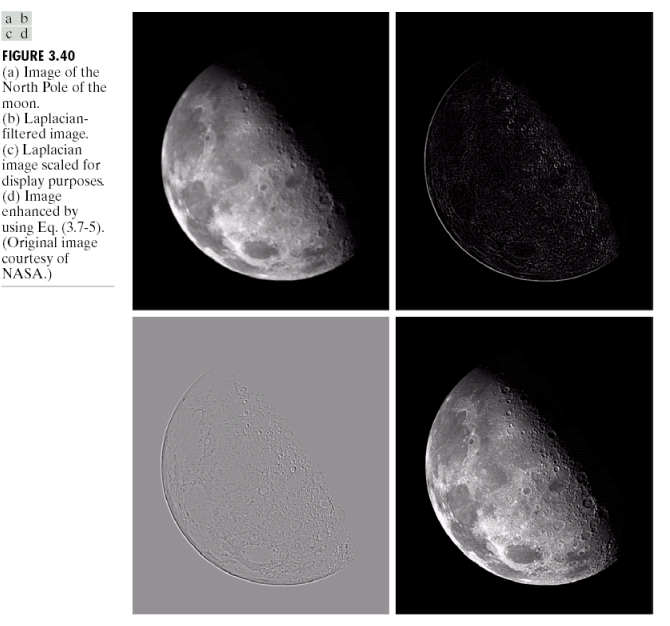
目标:对灰度变换以及精细细节进行增强,实现旋转不变性。
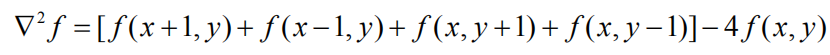
拉普拉斯算子对应的kernel: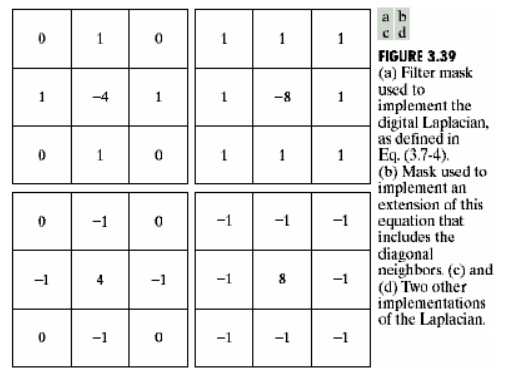
普通拉普拉斯kernel其具有90°的选择不变性;
- 右边两个扩充了对角线,具有45°选择不变性;(对对角线也求取导数)
通过拉普拉斯kernel求取了拉普拉斯分量之后加到原像素值得到响应: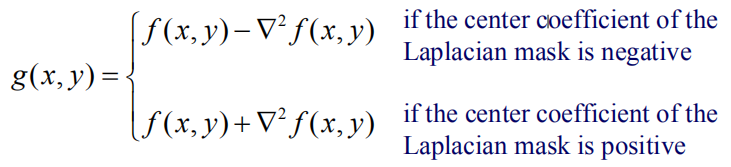
合并分量求取和分量合并:
从而设计kernel如下: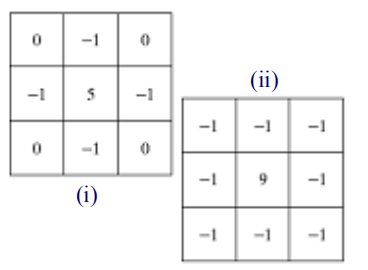
反锐化掩膜和高频提升滤波器



其kernel设计如下: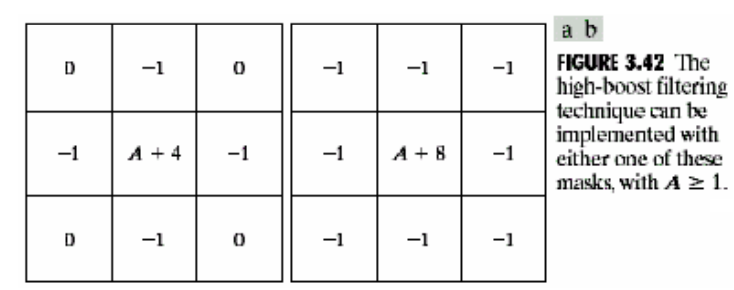
其实拉普拉斯算子方式的一般化,当时退化为拉普拉斯算子方式。
一阶梯度增强
我们只关注梯度的幅值,并为了减少计算量,梯度算子定义如下: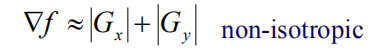
考虑窗:

Prewitt 算子