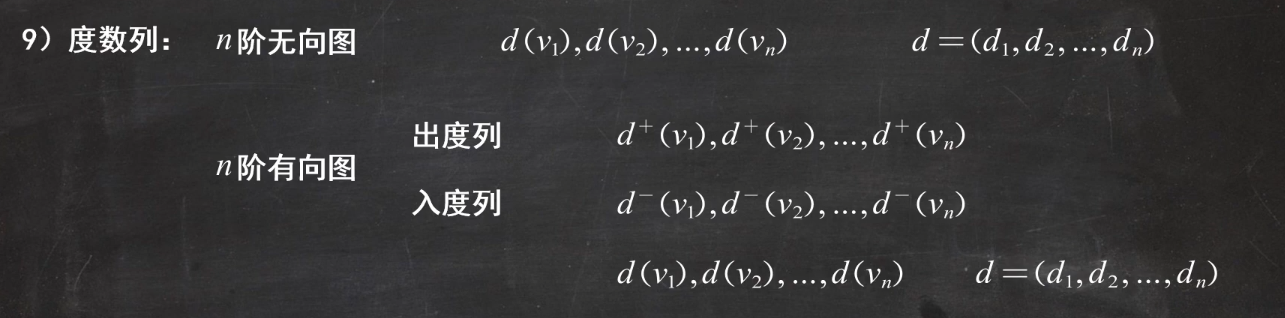image.png

1. 图

  • 图可以按照边的是否有方向分为无向图和有向图。无向图中的边使用(v1,v2)来表示，其中v1,v2的顺序是可以调换的，因为无向图的边不存在方向。有向图中的边使用<v1,v2>来表示，并且顺序是不可以调换的，因为有向图中的边是具有方向性的。
  • 图的阶数即是图中的顶点数，n个顶点的图就被称为n阶图。
  • 零图：一条边也没有的图。平凡图表示1阶零图。
  • 度
    • 无向图的度：顶点V作为边的端点的次数，记作🎁九、图的基本概念 - 图2
    • 有向图的度
      • 出度：顶点V作为边的始点的次数，记作🎁九、图的基本概念 - 图3
      • 入度：顶点V作为边的终点的次数，记作🎁九、图的基本概念 - 图4

image.png

  • 握手定理：
    • 在任何无向图中，所有顶点的度数之和等于边数的两倍，也等于图的阶数的两倍
    • 在任何有向图中，所有顶点的度数之和等于边数的两倍，所有顶点的入度之和等于所有顶点的出度之和，并且都等于边数
    • 推论：在任何图中，奇度顶点的个数是偶数

image.png

  • 度数列：用来表示每一个点的度数的序列
    • n阶无向图：
    • n阶有向图：分为入度列和出度列

image.png

例题：求出度序列

image.png

  • 度数列可图化的条件：
    image.png

    例题：可图化的度数列

    在此无向图中，前4个定点的度数之和已经是10，是偶数，那么根据可图化的条件，最后一个节点的度数也得是偶数才可，所以本题选D
    image.png
    要能作为4阶无向简单图的度序列，首先要求度数列的和是偶数，并且最大度必须小于等于无向图阶数-1
    image.png

  • 无向完全图：n阶无向完全图的边的条数为n(n-1)/2

2. 通路与回路

通路：无向图G中顶点和边的交替序列
回路：如果通路的起点和终点相同，那么就是一条回路
image.png

3. 图的连通性

连通：如果图中的两个顶点u,v之间存在通路，那么就称这两个顶点之间是连通，记作u~v
连通图：如果无向图是平凡图或者任何两个顶点都是连通的，那么这个就是连通图
可达：对于有向图G=<V,E>，对于u,v∈V，如果u到v之间存在通路，那么就称u到v是可达的，如果u和v之间互相存在通路，那么就称u和v是相互可达的

连通分类：
设G=<V,E>是有向图

  • 强连通图：任何两个结点之间是相互可达的
  • 单向连通图：任意两个结点至少从一个结点到另一个结点是可达的
  • 弱连通图：在略去有向边的方向之后，得到的图是连通 的

    例题：图的强弱联通判断

    image.png

4. 图的矩阵表示

4.1 关联矩阵

4.1.1 无向图中关联矩阵的定义

image.png
image.png

4.1.2 有向图中关联矩阵的定义

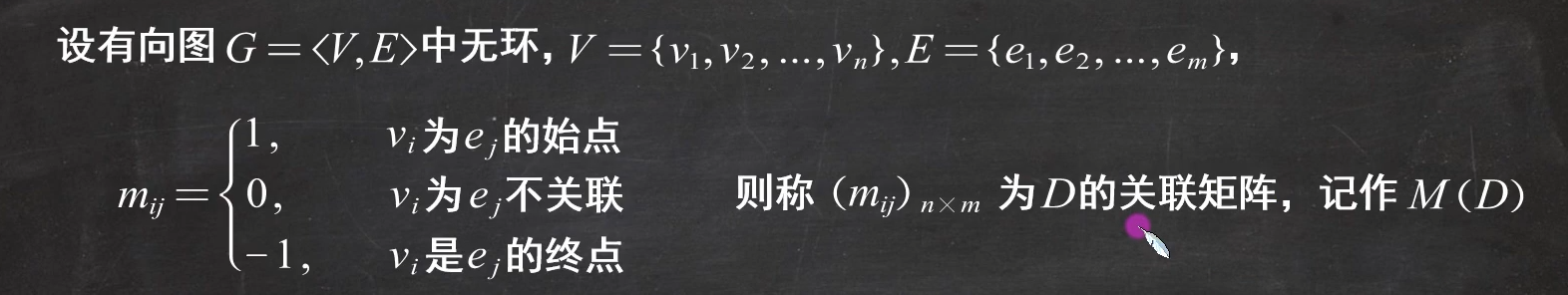
image.png

image.png

4.2 邻接矩阵

邻接矩阵中每一个点存的值表示的是两个顶点之间边的条数

4.2.1 有向图的邻接矩阵

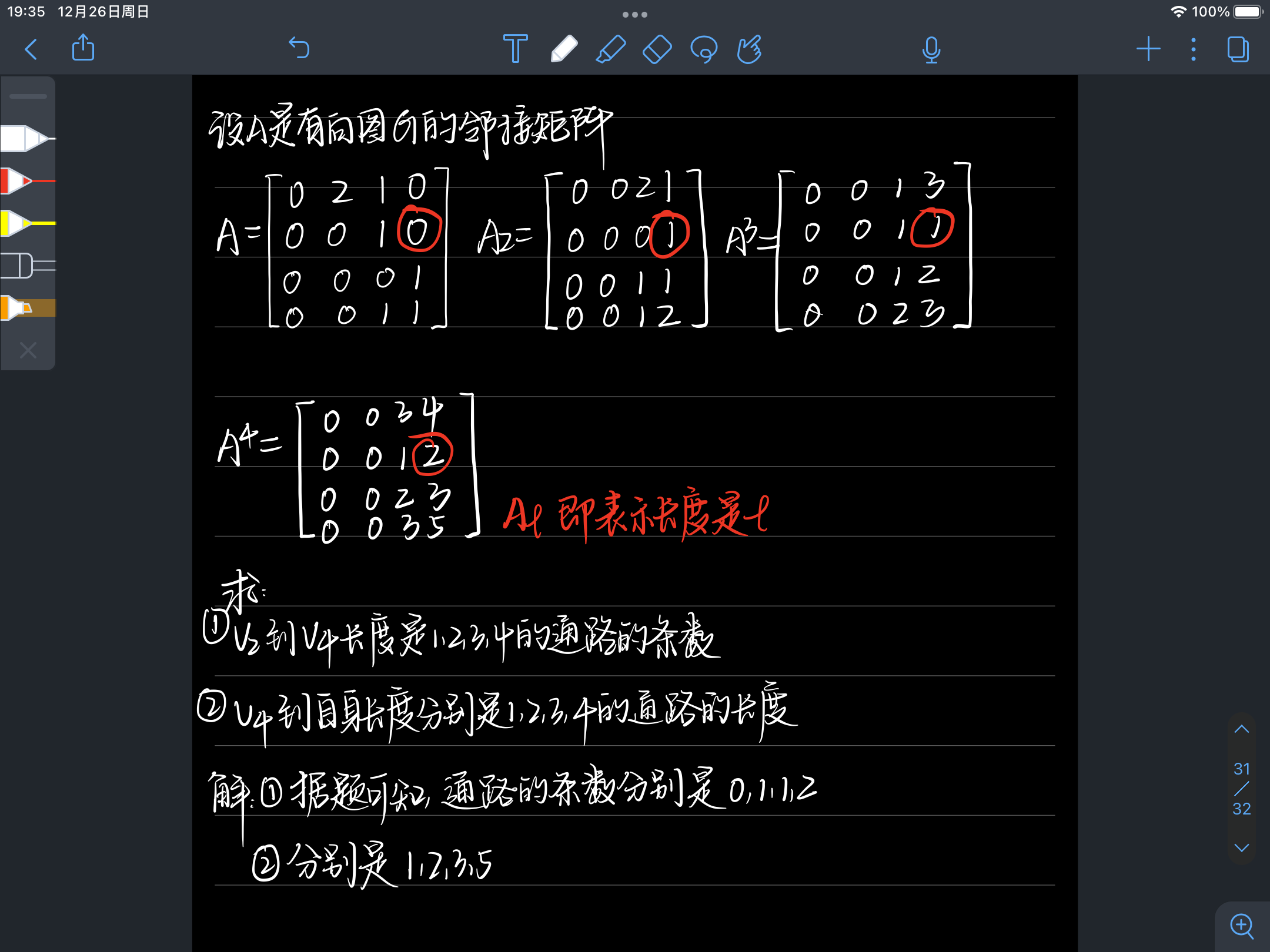
image.png
image.png

4.2.2 使用邻接矩阵来计算图中的通路和回路

image.png
image.png

4.3 可达矩阵

如果一个顶点到另外一个顶点是可达的，那么对应矩阵中的点值就为1，否则就为0。
规定：一个点到自身是可达的，所以可达矩阵对角线上的元素值都为1
image.png