✨ 题目：

在给定的网格中，每个单元格可以有以下三个值之一：

• 值 0 代表空单元格；
• 值 1 代表新鲜橘子；
• 值 2 代表腐烂的橘子。

每分钟，任何与腐烂的橘子（在 4 个正方向上）相邻的新鲜橘子都会腐烂。
返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1。

✨ 样例：

样例1：

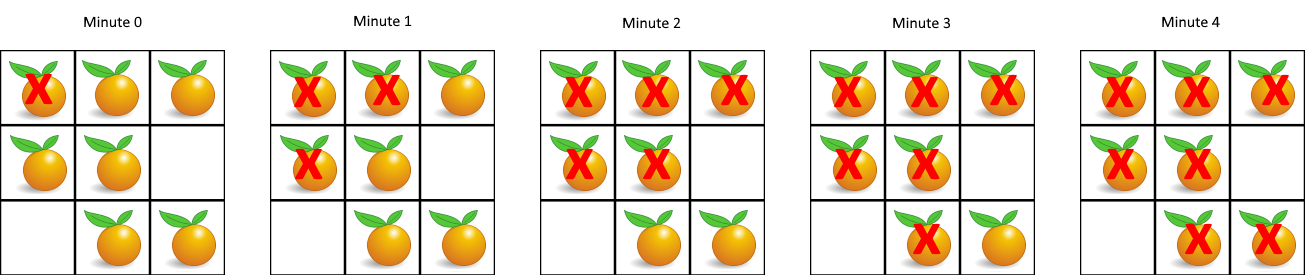
输入：[[2,1,1],[1,1,0],[0,1,1]] 输出：4

样例2：

输入：[[2,1,1],[0,1,1],[1,0,1]] 输出：-1 解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个正向上。

✨ 提示：

1. 1 <= grid.length <= 10
2. 1 <= grid[0].length <= 10
3. grid[i][j] 仅为 0、1 或 2

✨ 解答：

分析：

根据题意可以知道，橘子腐烂是按照层次去腐烂的，也就是说：每一分钟都会腐烂一层橘子。根据这个关系不难想到用广搜去解决。从给定的腐烂橘子开始，每次都向外拓展一层。判断橘子能否腐烂完，只需要先把新鲜的橘子数目 统计出来，然后腐烂一个就减1，最后判断数目是否大于0（不能腐烂完）即可。

AC代码：

class Solution {
    int _next[4][2] = {{-1,0},{1,0},{0,1},{0,-1}};
    // int dirc_x[4] = {0,1,0,-1};
    // int dirc_y[4] = {1,0,-1,0};
    int time[10][10];
    int cnt;
public:
    int orangesRotting(vector<vector<int>>& grid) {
        cnt = 0;
        queue<pair<int,int>> Q;
        memset(time,-1,sizeof(time)); // 默认花费的时间为-1
        int n = (int)grid.size(), m = (int)grid[0].size(),ans = 0;
        for(int i = 0;i < n;i++){
            for(int j = 0;j < m;j++){
                if(grid[i][j] == 2){
                    Q.push(make_pair(i,j));
                    time[i][j] = 0;
                }else if(grid[i][j] == 1){
                    cnt ++;  // 统计新鲜的橘子数目
                }
            }
        }
        while(!Q.empty()){
            // 依次取出腐烂的橘子
            pair<int,int> orange = Q.front();
            Q.pop();
            for(int i = 0;i < 4;i++){
                int next_x = orange.first + _next[i][0];
                int next_y = orange.second + _next[i][1];
                if(next_x < 0 || next_y < 0 || next_x >= n || next_y >= m || ~time[next_x][next_y] || !grid[next_x][next_y]){ // 如果越界了
                    continue;
                }
                time[next_x][next_y] = time[orange.first][orange.second] + 1;
                Q.push(make_pair(next_x,next_y)); // 存进来
                // 判断是否腐烂完
                if(grid[next_x][next_y] == 1){
                    cnt --;
                    ans = time[next_x][next_y];
                    if(!cnt){ //腐烂完了
                        break;
                    }
                }
            }
        }
        return cnt ? -1 : ans;
    }
};