一、循环队列

目的：充分利用空间， 防止数据出现“假溢出”的现象。将顺序队列的首尾相连，把存储队列的表看作是逻辑上的一个环，成为循环队列。
基本操作：

1. 判空：front = rear
2. 判满：front = (rear+1)%maxSize
3. 入队：rear = (rear + 1) % maxSize

4. 出队：front = front + 1

   二、栈

   定义：一种 只允许在表尾部进行插入和删除的线性表。
   注意：

5. 元素进栈以后可以立马出栈

6. 后进栈的元素一定先出栈
7. 栈遵循的规则是 先进后出

三、树和二叉树

1、二叉树的定义

1. 每个结点的度都不应该大于2

2. 每个结点的孩子结点次序不可以任意颠倒

   2、二叉树的性质

3. 在二叉树的第 i 层上至多有2^(i-1)个节点 (i >= 1)

4. 深度为 k 的二叉树至多有 2^k - 1的结点 (k >= 1)
5. 对任意一棵二叉树T，如果叶子节点（度为0）的数目为 n0，而度为2的结点数为n2，那么 n0 = n2 + 1

6. 具有 n 个结点的完全二叉树深度为 [log2n] + 1

   3、满二叉树

7. 定义： 深度为k且结点总数为 2^k - 1 的结点的二叉树。在满二叉树上，每一层结点数都是满的，即每层结点都具有最大结点数。

   4、完全二叉树

8. 定义：一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

   5、二叉树的存储结构

9. 顺序存储（用数组下标的关系来模拟二叉树父亲结点和儿子结点之间的关系）

10. 链式存储（每个节点具有两个指针域和一个数据域）

如果一个二叉树有n个结点，那么它的二叉链表中必定有2n个指针域，其中必有n+1个空的链域

6、二叉树的遍历和线索化

1. 二叉树的三种遍历方式
   1. 先序遍历
      1. 访问根节点
      2. 遍历左子树
      3. 遍历右子树
   2. 中序遍历
      1. 中序遍历左子树
      2. 访问根节点
      3. 中序遍历右子树
   3. 后序遍历
      1. 后序遍历左子树
      2. 后序遍历右子树
      3. 访问根节点
2. 三种遍历序列 => 根据对应的遍历方式可以得到对应的遍历序列
   1. 先序遍历可以得到先序遍历序列
   2. ……
   3. ……

3. 根据三种遍历序列来判断二叉树的原型

   1. 先序序列 + 中序序列
      1. 先序序列的第一个元素就是树的根结点。然后在中序序列中找到该根节点。该结点左侧序列即为根节点的左子树，右侧序列即为根节点的右子树。对分割出来的序列重复上述分析操作，即可完全确定一颗二叉树。
   2. 后序序列 + 中序序列
      1. 先由后序序列的最后一个元素可以确定出二叉树的根节点，然后在中序序列中找到分析出来的根节点的位置，中序序列中该结点左侧的即是根节点的左子树，右侧的是根节点的右子树。然后对分割出来的新序列重复上述操作，即可完全确定出对应的二叉树。

         7、哈夫曼树

         构造哈夫曼树

4. 先从序列中找出权值最小的两个数，然后将权值相加形成一棵树，然后构造出来的树作为新的数据加入到序列中。

5. 在新序列中重复上述操作，找到最小的两个数然后权值相加，形成一个新树。新树再作为新的数据加入到序列中。

   哈夫曼编码
   在构造的哈夫曼树的基础上添加编码，规则 左0右1， 如下图所示：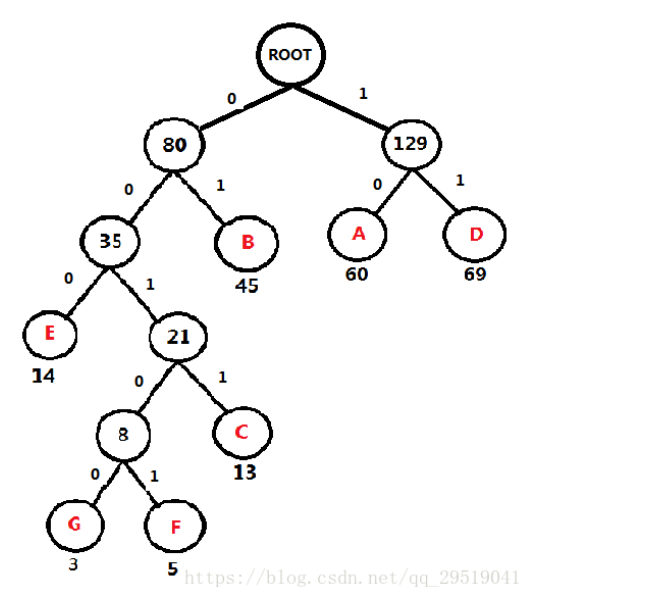
   
   各个数据对应的编码如图所示：
   **

四、图

1、图的存储方式

1. 邻接矩阵存储法 （顺序存储结构）
   • 定义：又称为数组法，采用一个二维数组来存储图中顶点和顶点之间的关系。
   • 方法：如果从二号点到三号点有一条有向路径可以到达，那么在二维数组中表示为 a[2][3] = 1，（如果是有向路径，那么应该还有a[3][2] = 1）。反之，如果两个点直接没有路径可以到达，那么在二维数组中应该对应的设置为0。
   • 优点：直观的反映图中各个点之间的关系。
   • 缺点：如果是边比较少的图，该存储方式会浪费大量的空间。
2. 邻接表表示法：（链式存储结构）

假如有如图所示的一张图：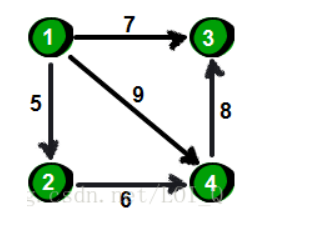
那么其邻接表存储方法为：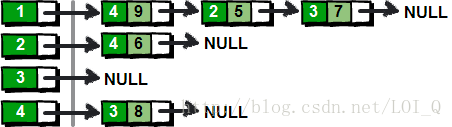
链式存储的优点

2、图中结点的度

1. 无向图的度：无向图中结点的度就是结点上线的条数（即点上有多少条线）
2. 有向图的度：有向图中结点的度就是该点的出度（即点上有多少条线是出去的）

   3、图的两种遍历方式

• 深度优先遍历

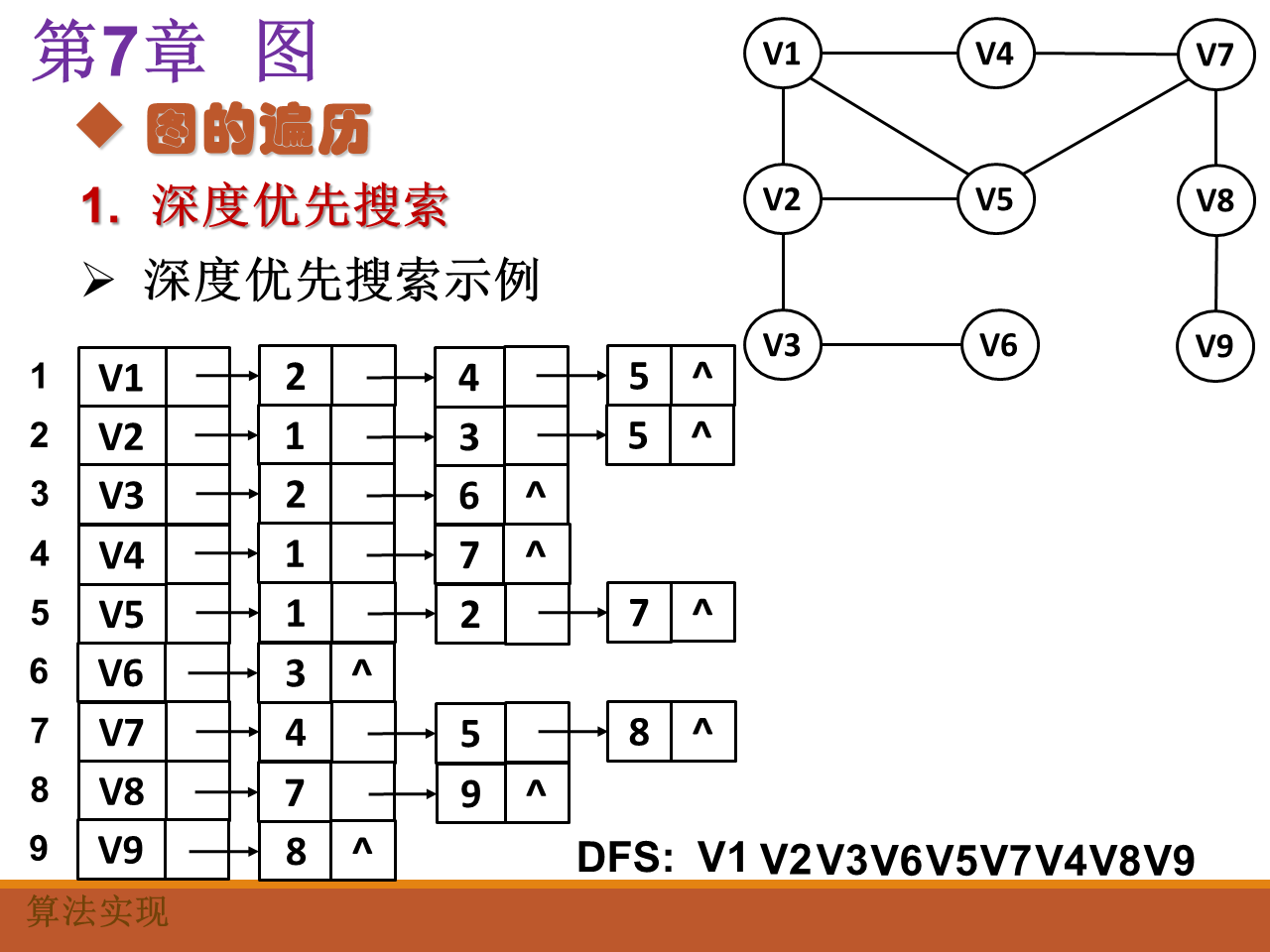
先从第一个点开始遍历，然后之后遍历到未访问过的顶点就进入到以该顶点为起点的链表进行遍历。一直向下遍历，直到不能遍历为止
**

• 广度优先遍历

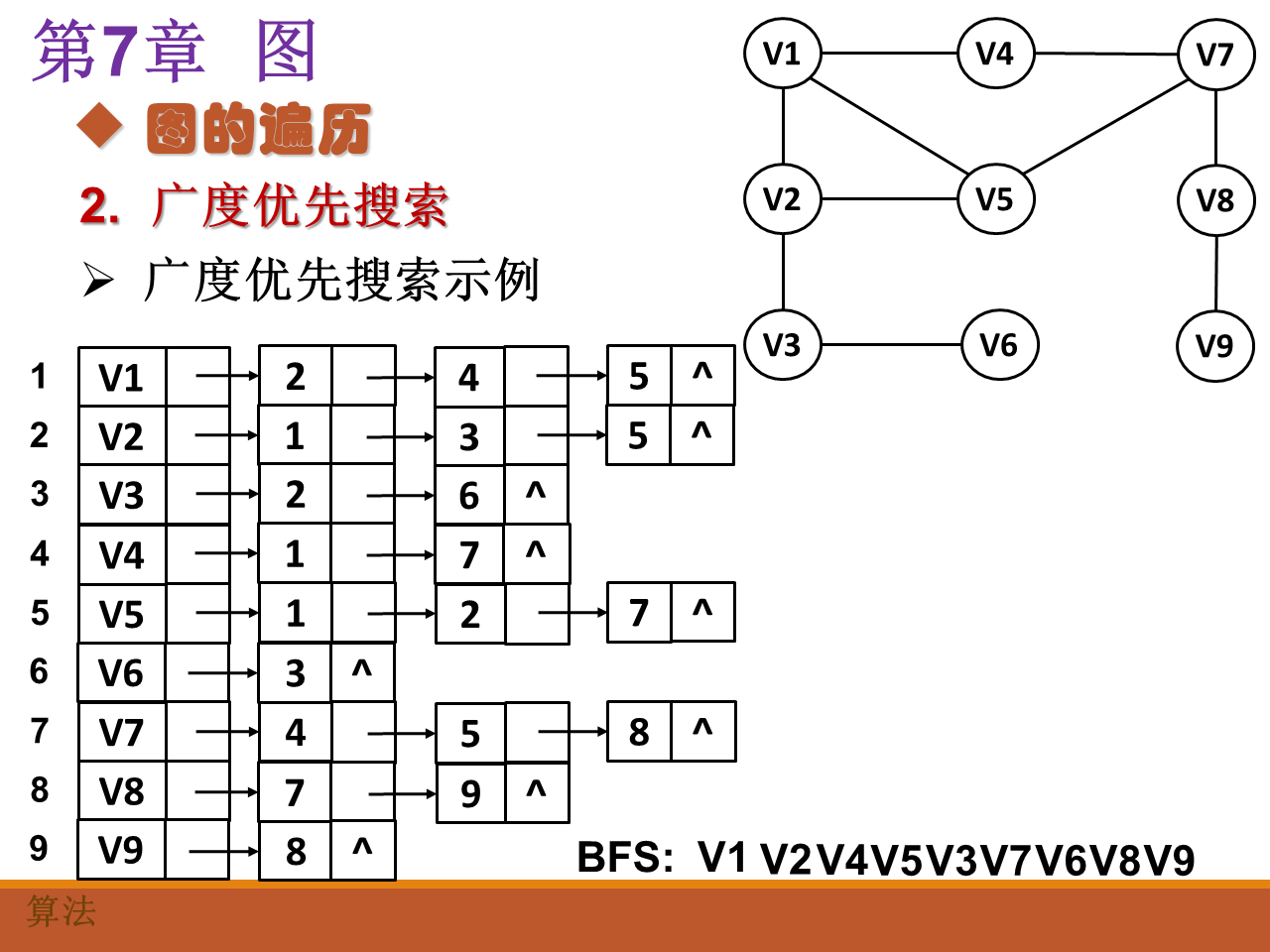
广度优先遍历体现的是 层 的遍历思想。遍历到第一个点V1的时候，把V1一步能到达的所有点都加入到队列中。加入完成以后，将V1出队，标识为该点已经遍历过。然后对队列中的其他点依次执行此操作，最后即可得到广搜的遍历序列。

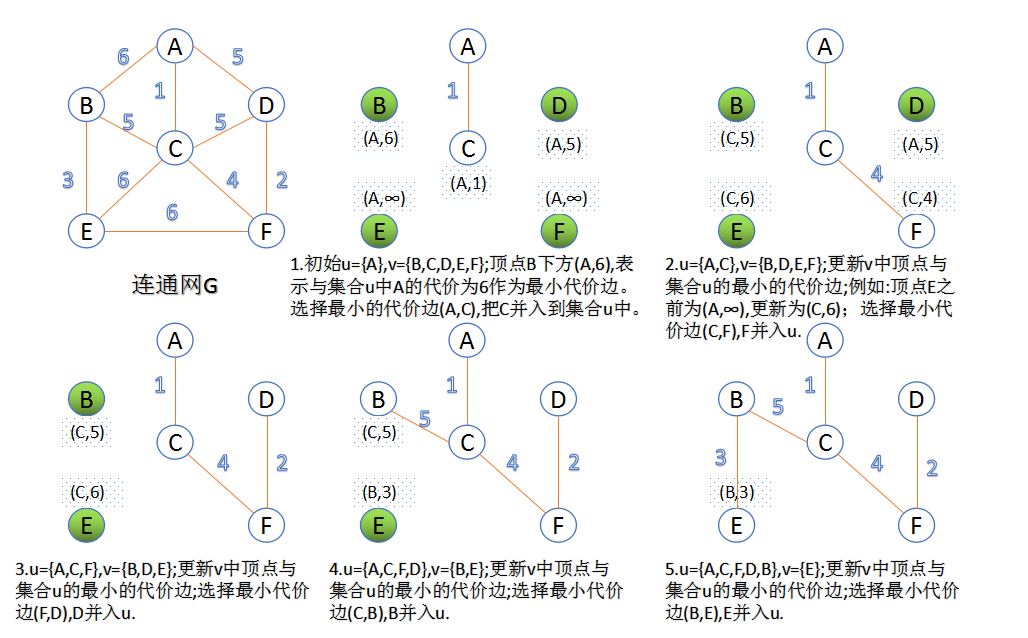
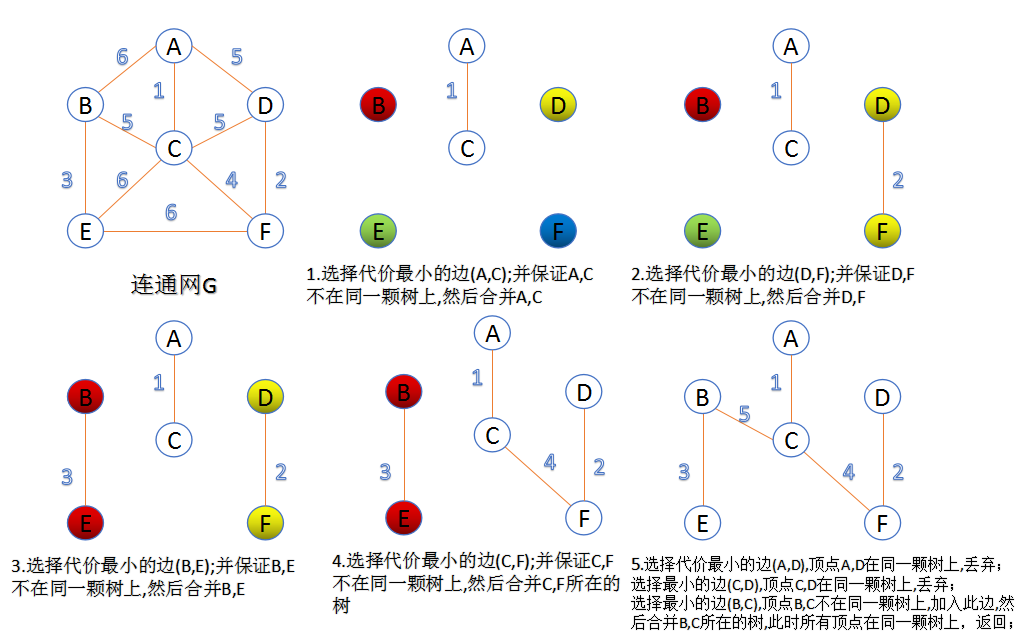
4、最小生成树

定义：在一个连通网的所有最小生成树中，各边的代价之和最小的那棵生成树称为该连通网的最小生成树，简称为 最小生成树。
生成最小生成树的算法：

1. 普利姆算法（Prim） => 加点法

2. 克鲁斯卡尔算法（Kruskcal） => 加边法·

   5、拓扑排序

   注意：有向无环图（DAG图）才有拓扑排序。
   方法：

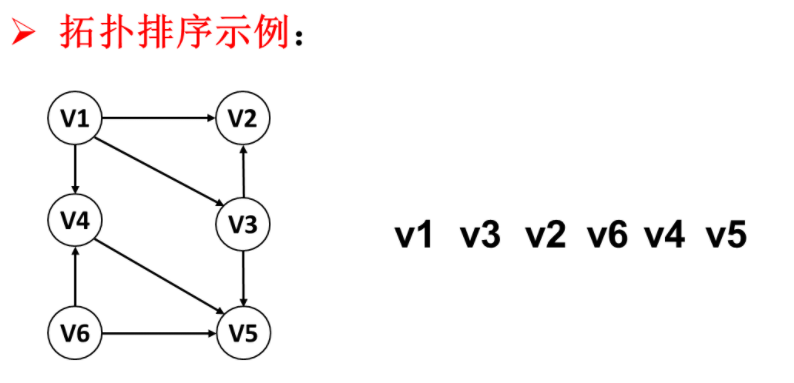
1. 从 DAG 图中选择一个 没有前驱（即入度为0）的顶点并输出。
2. 从图中删除该顶点和所有以它为起点的有向边。
3. 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

一个DAG图可以有一个或多个拓扑排序序列

6、最短路径算法

1. 求某一个顶点到其他各个顶点的最短路径问题

方法：Dijkstra算法
思想：要缩短两个点之间的路径，就需要找到第三个点。
时间复杂度：O(N^2)

1. 求任意一对顶点间的最短路径

方法：Floyd算法
时间复杂度：O(N^3)
**

五、查找

1、线性表的查找

1.1 顺序查找法

用所给关键字和线性表中的各元素的关键字逐个比较，直到成功或者失败。
存储结构为顺序结构或链式结构。
顺序查找法查找成功的平均查找长度为：1/2 * (n + 1)
查找失败的平均查找长度为：1/2 * n

1.2 折半查找法

折半查找法也叫二分查找法，使用这种方法有两个要求：

1. 必须采用顺序存储结构
2. 待查找的列表必须按关键字大小有序排列

   1.3 分块查找法

   2、基于树的查找法

   2.1 二叉排序树

1. 二叉排序树的规则
   1. 如果左子树非空，那么左子树上的所有结点的值都小于根节点的值。
   2. 如果右子树非空，那么右子树上的所有结点的值都大于根节点的值。
   3. 左右子树均为二叉排序树。
2. 二叉排序树的插入和创建
   1. 如果树为空树，那么key成为二叉排序树的根。
   2. 如果树不为空树
      1. 如果key等于根节点的值，就停止插入。
      2. 如果key小于根结点的值，就将key插入左子树。
      3. 如果key大于根节点的值，就将key插入右子树。
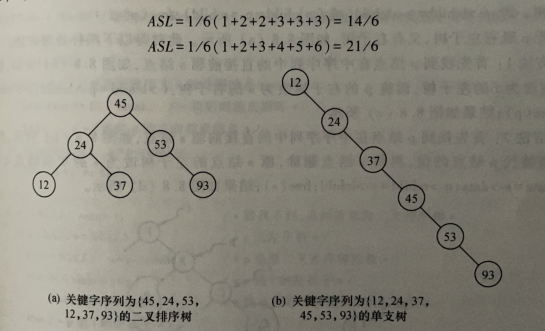
3. 二叉树的平均查找长度

3、哈希查找

3.1 基本思想

在元素的关键字k和元素的存储位置p之间建立起一个对应关系H(k)的单元，以后查找关键字为k的元素时，再利用哈希函数直接计算出该元素的存储位置 p = H(k)即可。

3.2 哈希表的建立

方法：除留余数法
假设哈希表长度为m，p为小于等于m的最大素数，那么哈希函数为：
H(k) = k % p

3.3 处理哈希冲突

1. 开放定址法 （再散列法）
   1. 线性探测再散列
      1. di = 1,2,3,4…m-1
   2. 二次探测再散列
      1. di = 1,-1,4,-4,9,-9…,k^2,-k^2
   3. 伪随机探测再散列
      1. di = 伪随机数序列
2. 链地址法

3.4 哈希查找的平均查找长度

六、排序

1、直接插入排序

![image.png](https://cdn.nlark.com/yuque/0/2021/png/21436600/1625188072888-62e0c3c5-8176-4ccf-a145-01f27fbefbae.png#align=left&display=inline&height=267&originHeight=534&originWidth=1266&size=86796&status=done&style=none&width=633)

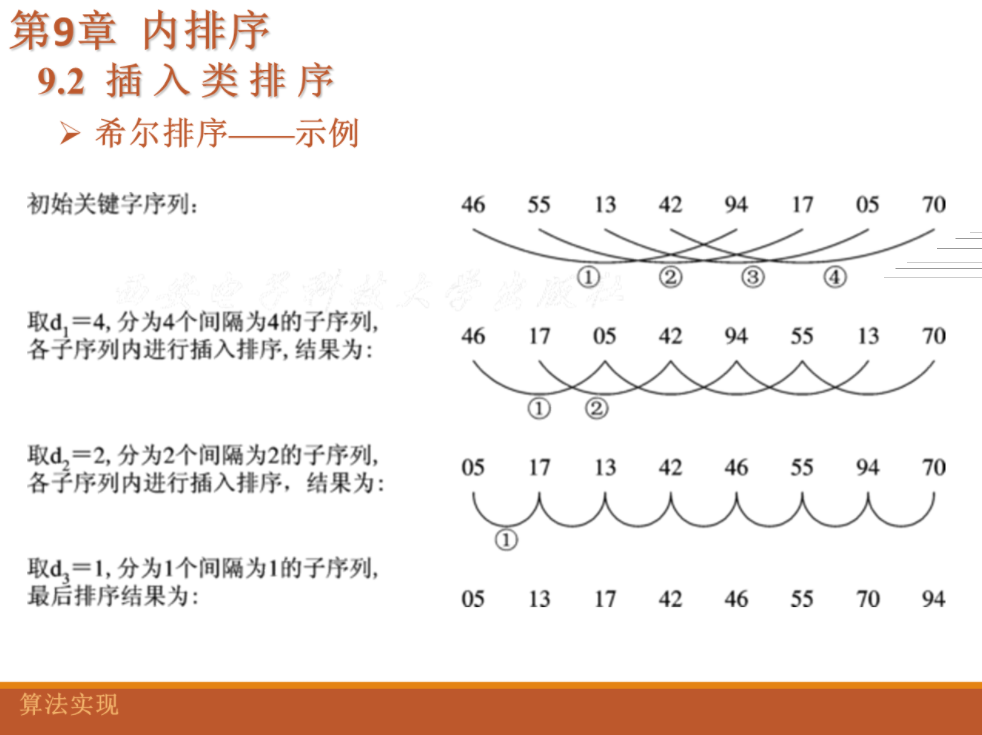
2、希尔排序

3、冒泡排序

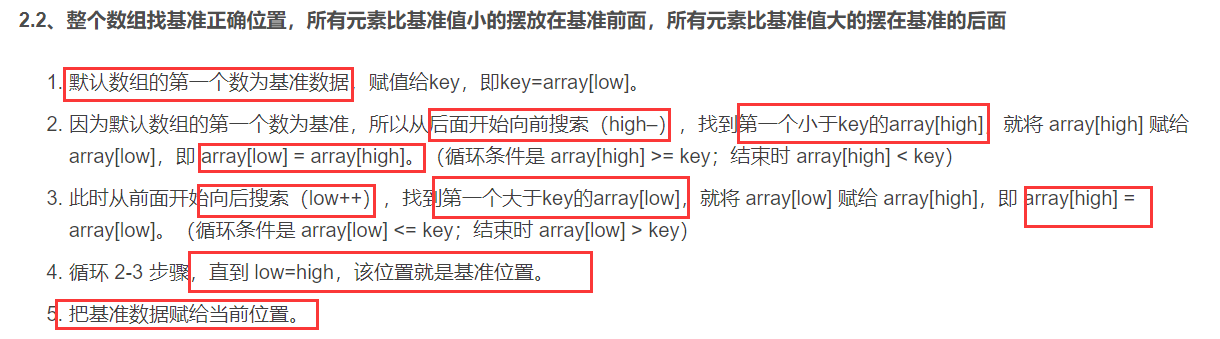
4、快速排序

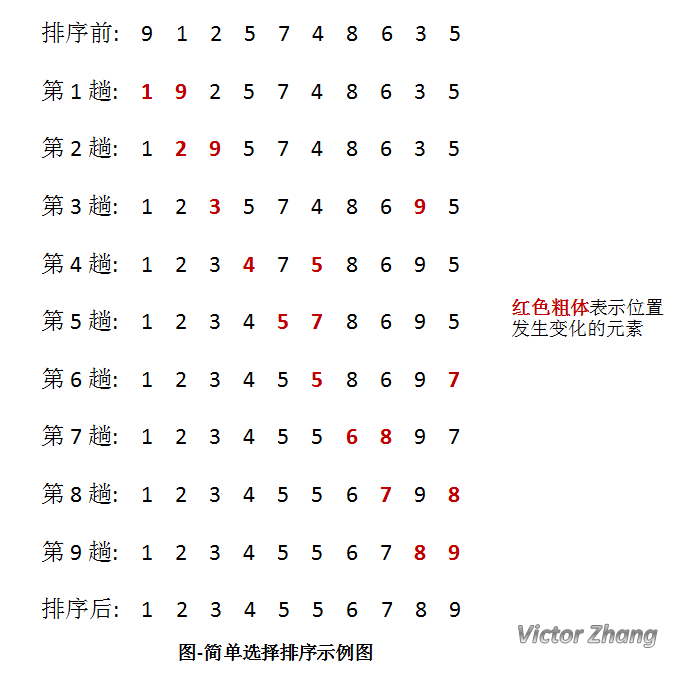
5、简单选择排序