二分分类

Binary Classification：二分分类，其特点是事情的结果有且仅有两个
比如：

• 某个名字对应的是女性还是女性
• 某张图片是否是一张猫图
• 某个人是否患有某种疾病

  诸如上述的问题，都有一个共同点：问题的结果大抵都只有“是”或者“不是”这两种情况，正好对应二分分类的特点：事情的结果有且仅有两个。

而我们的学习算法要做的，就是学习数据，训练出一个“分类器”，从而能够对其他的一些情况，进行合理的分类。（比如较为准确的判断出，一张图是否是猫图）

Logistic回归

逻辑回归（Logistic Regression）（一）
Logistic回归，也就是逻辑回归，是一种用于解决二分类的学习方法，用于估计某种事物的可能性
逻辑回归与线性回归：逻辑回归和线性回归都是一种广义的线性模型。逻辑回归与线性回归存在很多相似之处，如果逻辑回归没有sigmoid映射函数的话，其实也是一种线性回归。逻辑回归通过sigmoid映射函数引入了非线性因素，从而可以很好的处理0/1分类的问题

逻辑函数sigmoid

逻辑函数：
函数曲线如下所示：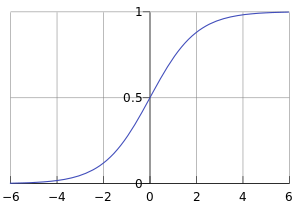

从上图可以看出来，Sigmoid函数是一个范围从0~1的一个曲线，取值在[0,1]之间

其中，是我们的输入，是我们所需要取的参数

对于二元分类问题来讲，一般给定一个输入特征向量，而我们要做的就是设计一个合适的函数，来计算并得出。

结合实际来看，特征向量对应的就是样本（比如一张图片），就是表示等于1的可能性或者机会。 假设是一个nx维度的向量，那么就表示样本一共有nx个特征。

我们用来表示逻辑回归的参数，其也是一个nx维向量（表示每一个特征所代表的权重，因此和特征向量的维度相同），除此之外，还有一个参数b，这是一个实数，用来表示偏差

最之间想到的就是使用线性回归的方式进行拟合：

这感觉就是将每个特征乘以对应的特征权重，最后加上一个偏差系数。

但这种方式存在的问题是：

• 其实表示的是一种概率，因此取值应该在0~1之间，使用线性回归的方式，取值可能很大，也可能为负数。

因此处理方法是，将上面的线性回归的函数，作为自变量，成为sigmoid函数的因变量，从而将线性函数转换为非线性函数，并且将值域从实数转换到0~1之间

代价函数

代价函数：已找到最优解为目的的函数

比如上面我们所提到的，就是一种代价函数，通过在给定的训练集上进行训练，最后找到合适的w和b，从而进行预测，得到输出。

损失函数

:::info 我们通过代价函数，所计算出来的其实是实际结果的预测（预估），那么不难想到，损失函数就是评估预测结果和实际结果之间的差距。 :::

当然希望预测结果和实际结果越接近更好，因此损失函数的值越小，说明模型的拟合度越好

我们一般采用预测值和实际值的平方差或者平方差的一半，但我们在逻辑回归中并不这么做，因为当我们在学习逻辑回归参数的时候，使用这种方式会导致我们的函数出现凹陷，从而出现多个局部最优解，导致梯度下降法可能找不到全局最优值。
因此，我们在逻辑回归中使用到的损失函数是：

• 当的时候，损失函数，为了让损失尽可能的小，那么就需要尽可能大，而表示的其实是一种概率，所以会无限接近于1
• 当的时候，损失函数，因此就需要尽可能的小，所以会无限接近于0

课后习题

工作台 - Heywhale.com