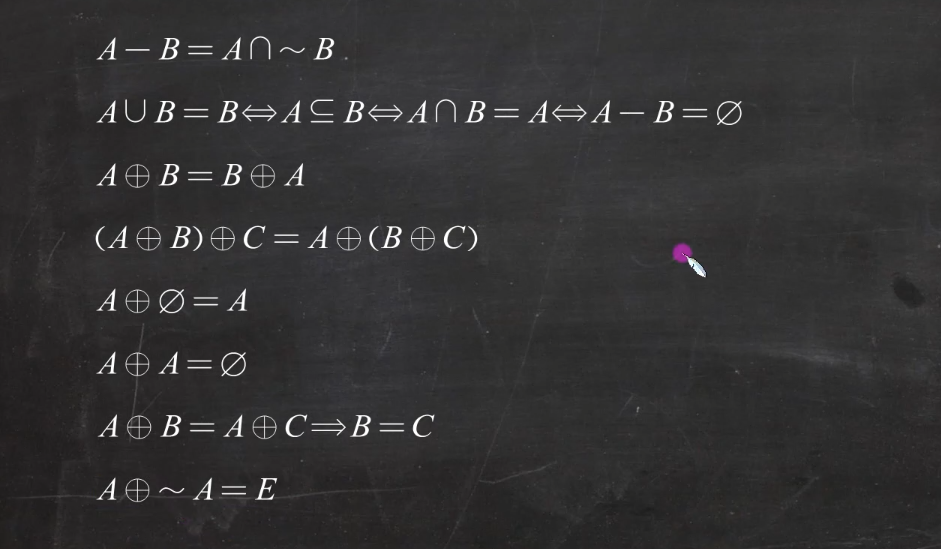一、命题符号化

做题步骤：

1. 分析题目意思，将题目描述变成一个个简单命题。
2. 将条件和结论都使用简单命题表示

3. 根据结论的形式选取合适的证明方法

   1. 普通证明法：直接从前提推导到结论
   2. 附加前提法：适用于结论是蕴涵式的题目。将蕴涵左边的命题当作条件来使用，证明出蕴涵右边的命题即可，称为附加前提引入
   3. 归谬法：将结论的否定作为前提引入，在推理的过程中，推出和当前给定的前提矛盾的部分，从而证明原来的结论是正确的的。

      1、命题逻辑的推理证明

      练习题1：

      

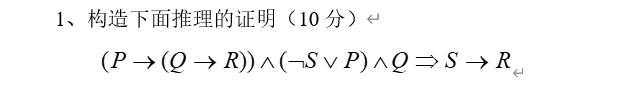
      练习题2：

      

      练习题3：

      

      2、谓词逻辑的推理证明

      练习题1：

      

      练习题2：

      二、析取范式和合取范式

      简单析取式：仅由有限个文字构成的析取式
      简单合取式：仅由有限个文字构成的合取式
      析取范式：仅由有限个合取范式的析取构成的命题
      合取范式：仅由有限个析取范式的合取构成的命题

      练习题：

      练习题1：

      

      练习题2：

      

      练习题3：

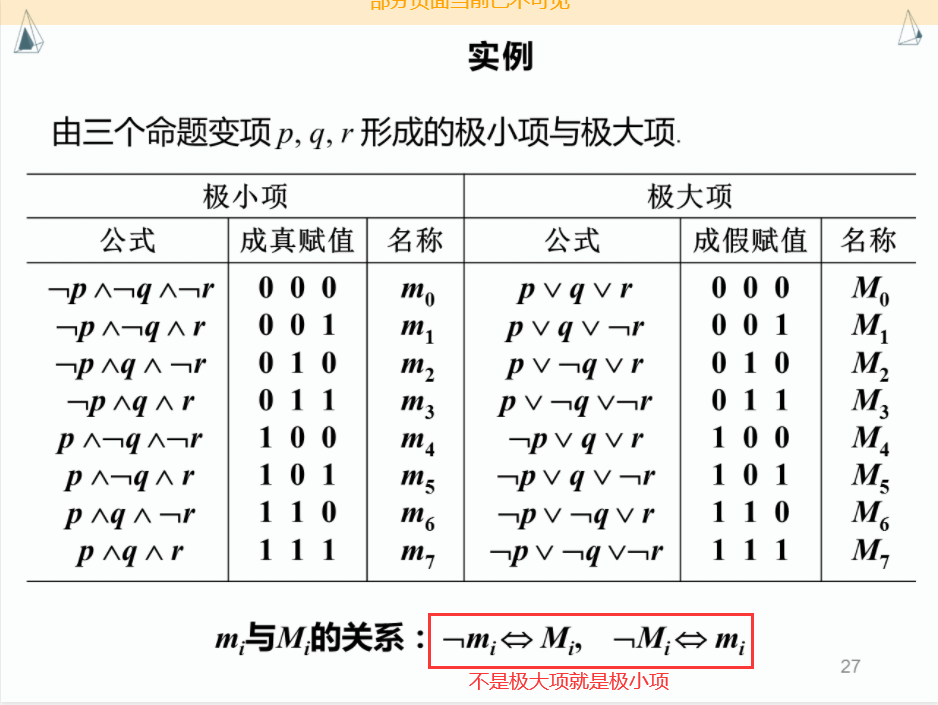
      三、极大项和极小项

      极小项：

4. 简单合取式

5. 每个命题变元和它的否定恰好出现且仅出现一次
6. 命题变元或它的否定式按照下标从小到大的顺序排列

极大项：

1. 简单析取式
2. 每个命题变元和它的否定恰好出现且仅出现一次
3. 命题变元或它的否定式按照下标从小到大的顺序排列

四、集合代数

集合的基本概念：

• 集合：把一些事物汇集在一起组成一个整体，就称为是集合。这些事物就是这个集合中的元素或者成员。元素和集合之间的关系是隶属关系，即只有属于或不属于，属于记作，不属于记作
• 子集：设A,B是两个集合，如果B中的每一个元素在A中都能够找到，那么就称B是A的子集，记作
• 相等：如果，那么就称A和B是相等的，记作
• 真子集：如果，那么就称B是A的真子集
• 空集：不包含任何元素的集合称之为空集，空集是一切集合的子集
• n元集：含有n个元素的集合称为是n元集，它的含有m(m<=n)个元素的子集称作它的m元子集
• 幂集：设A是一个集合，将A的全体子集构成的集合我们称之为A的幂集，记作P(a)
• 全集：在一个具体的问题中，如果涉及到的集合都是某个集合的子集，那么就称这个集合为全集，记作E

集合间的运算：

• 并运算：
• 交运算：
• 差运算：
• 对称差运算：
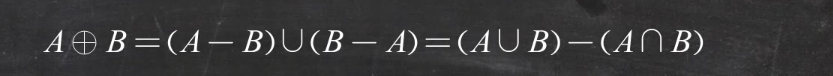
• 绝对补集：在全集E中，将集合A中的所有元素去除

包含排斥原理：

集合恒等式：

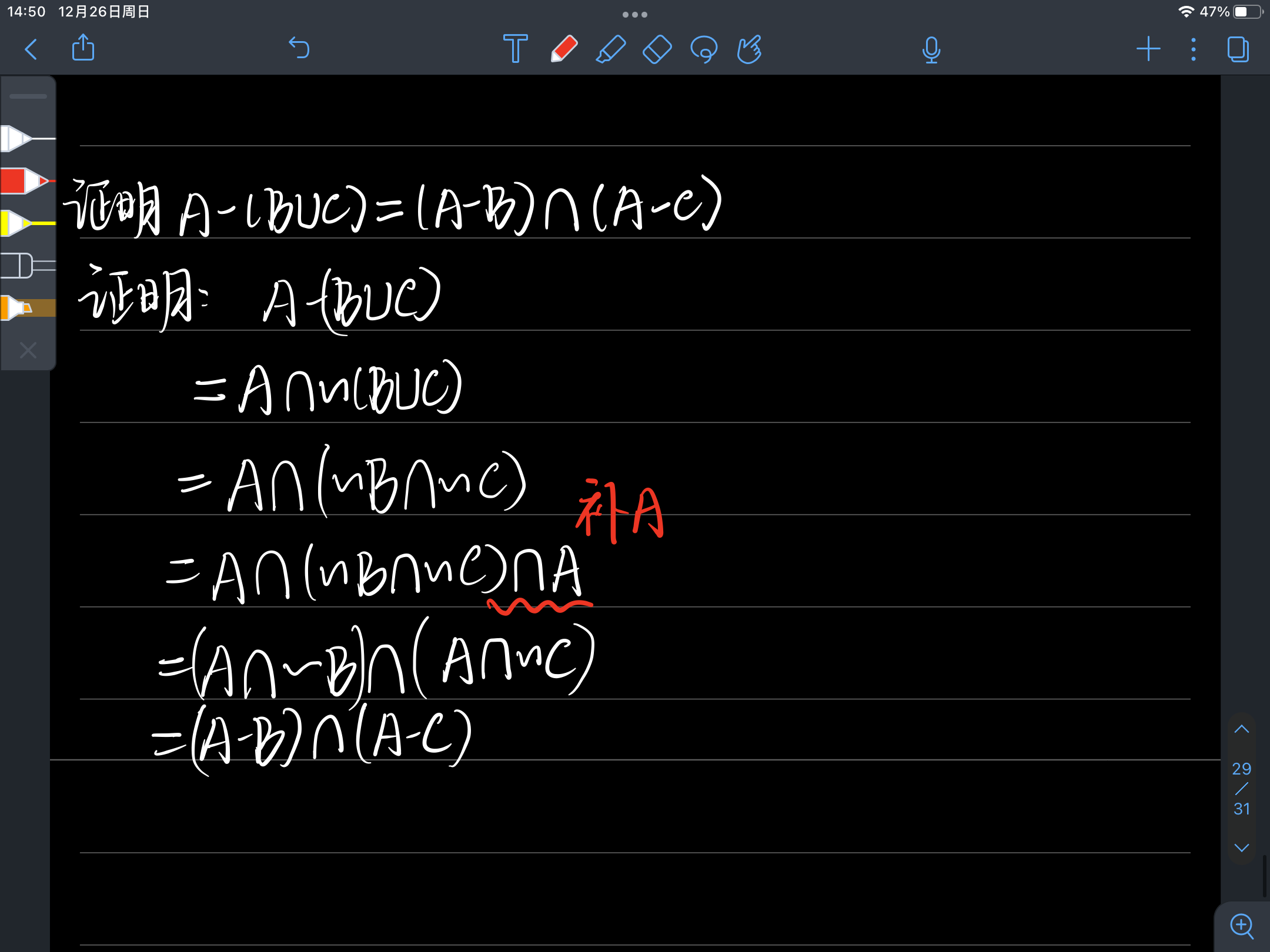
1. 集合恒等式

练习题1：

练习题2：

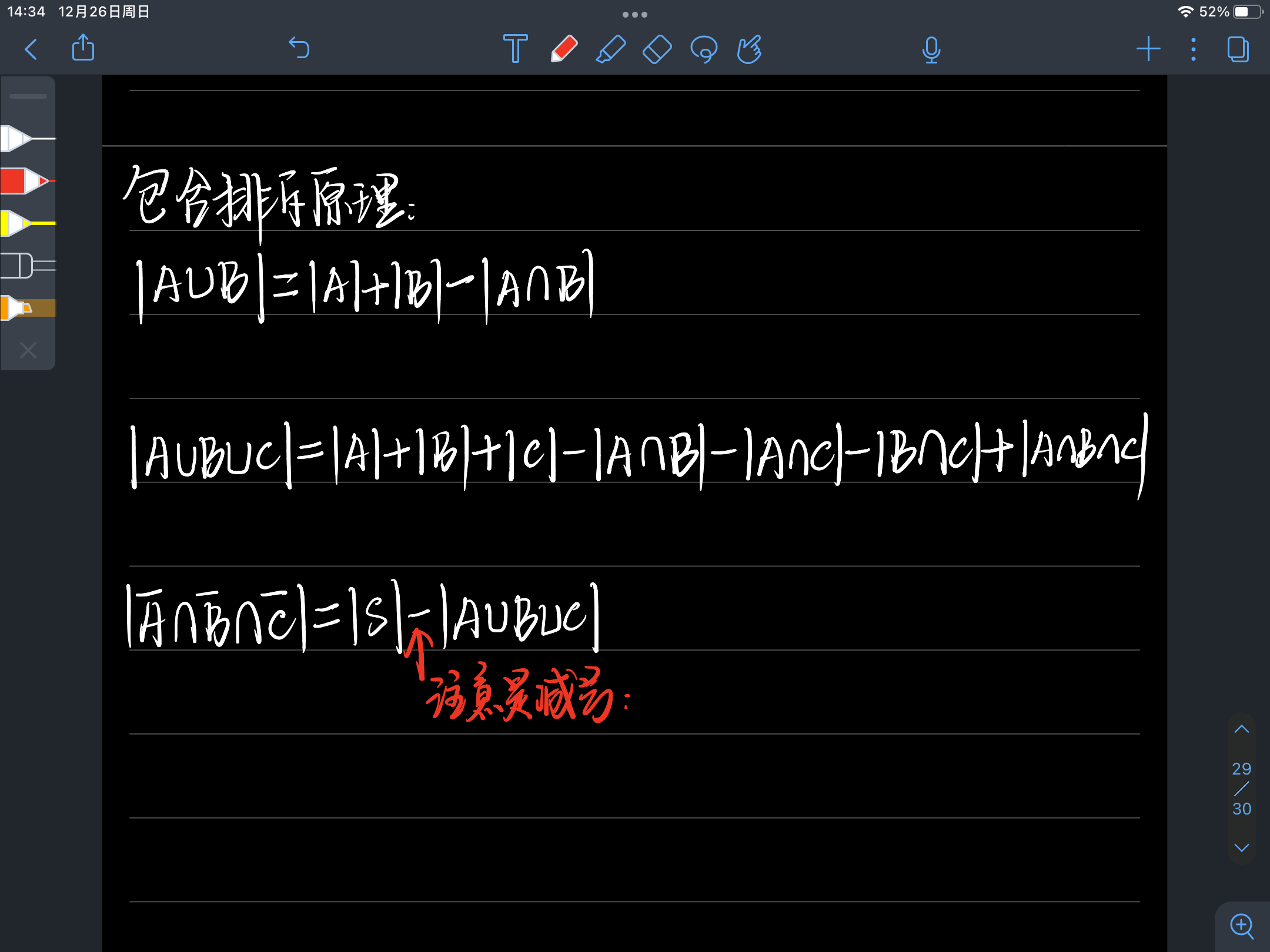
2. 包含排斥原理

练习题1：

练习题2：

练习题3：

五、二元关系（⭐⭐⭐⭐⭐）

笛卡尔积： 二元关系的表示方法：

• 集合表达式：使用有序对的方式进行表示
• 关系矩阵：使用一个二维的矩阵进行表示
• 关系图：使用有向线段构成的图进行表示

逆关系：有序对的前后两个元素反转顺序 右复合： 二元关系的性质：

• 自反
• 反自反
• 对称
• 反对称
• 传递

关系的闭包：设R是非空集合A上的关系，R的自反（对称或传递）闭包是A上的关系R’，使R’满足以下条件： 等价关系：设R是非空集合A上的关系，如果R是自反的、对称的和传递的，那么就称R为A上的等价关系 等价类：等价类是集合A中有相同性质R的元素组成的一类集合 商集：设R为非空集合A上的等价关系，以R的所有等价类作为元素的集合称为A关于R的商集，记作A/R 划分： 偏序关系：设R为非空集合A上的关系，如果R是自反的、反对称的和传递的，那么就称R是A上的偏序关系。 最大元和最小元： 极大元和极小元： 上界和上确界：

• 上界：对应哈斯图中大于等于子集中极大元层数的所有点
• 上确界：上界中的最小值

下界和下确界：

• 下界：哈斯图中小于等于极小元所在层数的所有点
• 下确界：下界中的最大值

1. 求解关系的闭包

练习题1：

2. 等价关系、等价类和划分

练习题1：

练习题2：

练习题3：

3. 二元关系之间的运算

练习题1：

4. 偏序集

练习题1：画哈斯图，求极大元极小元

六、图论（⭐⭐⭐⭐）

图：

• 按照边是否有方向可以分为有向图和无向图
• 图的阶数就是图中的顶点个数
• 顶点的度：
  • 无向图：顶点作为边的端点的次数
  • 有向图：分为入度和出度
    • 入度：顶点作为边的终点的次数
    • 出度：顶点作为边的起点的次数

握手定理：在图中，所有顶点的度数之和等于边数的两倍 度数列：用来表示每一个顶点的度数的序列。有向图还分为出度列和入度列 无向完全图：n阶无向完全图的边的条数为n(n-1)/2 图的矩阵表示：

• 关联矩阵：描绘的是图中的点和边的关系
  • 无向图：关联矩阵中的点表示的是顶点和边的关联次数
  • 有向图：如果该点和边没有关系，值就为0。如果是该边的起点，值就为1。如果是该边的终点，值就为-1。
• 邻接矩阵：描述的是图中点和点之间的关系。（只针对有向图）
  • 有向图：表示顶点A到顶点B的边的条数
• 可达矩阵：如果顶点A可以到达顶点B，那么对应矩阵中的值就为1，否则就为0。顶点到自身是可达的，所以对角线上的元素都为1

边连通度： 点连通度：

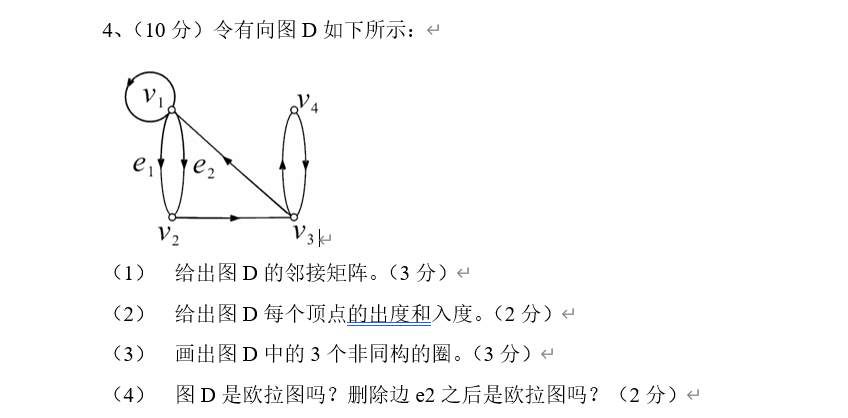
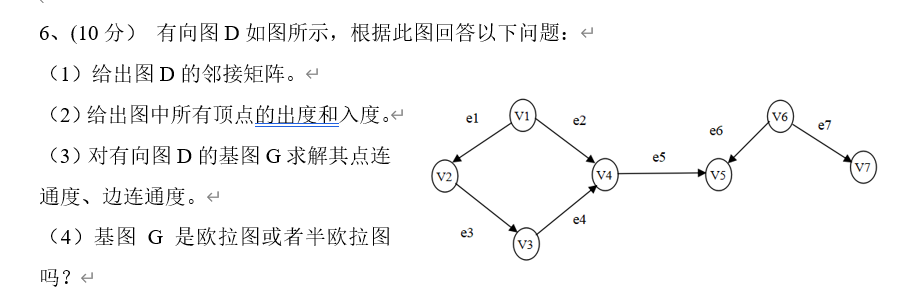
1、图的邻接矩阵

七、哈夫曼法求最优二叉树（⭐⭐⭐⭐）

一些相关概念

1. 子图：
2. 生成树：如果无向图G的生成子图T是树，那么就称T是G的生成树
3. 生成树的权：对于无向连通带权图，T是G的一棵生成树，T的各边权之和称为T的权，记作W(T)
4. 最小生成树：G的所有生成树中权最小的生成树

使用哈夫曼算法求最优二叉树 解题步骤：

1. 给权排序
2. 选出两个权最小的顶点，添加新点，权为两个点的和
3. 重复步骤1，2，直到只有一个顶点

二元前缀码：由0-1符号串构成的前缀码 最佳前缀码：由最优二叉树产生的前缀码。左孩子对应的边标记为0，右孩子对应的边标记为1

1、哈夫曼法

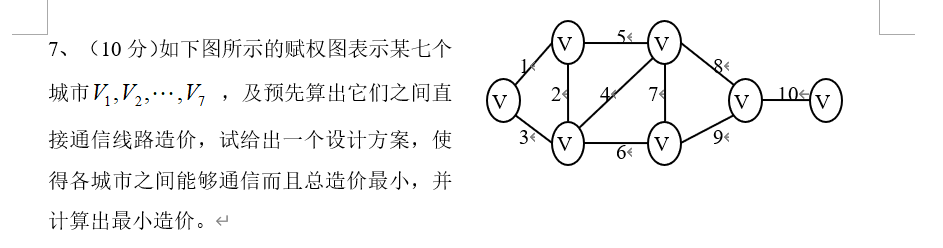
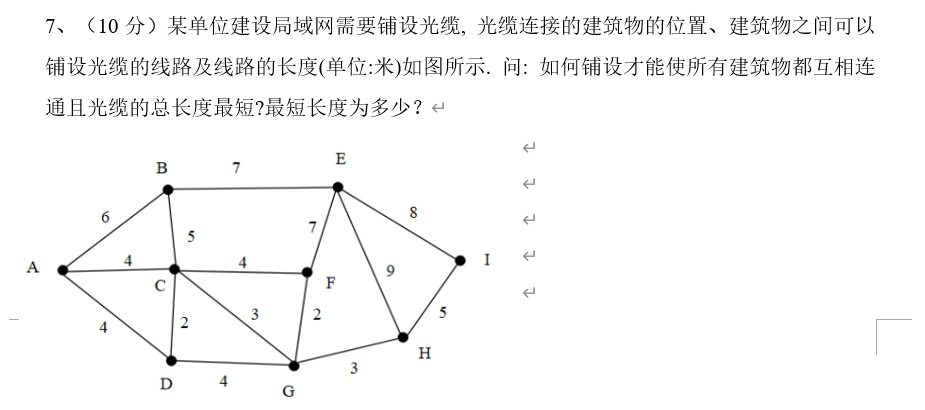
2、无向树的基本定义