✨ 题目：

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

✨ 示例：

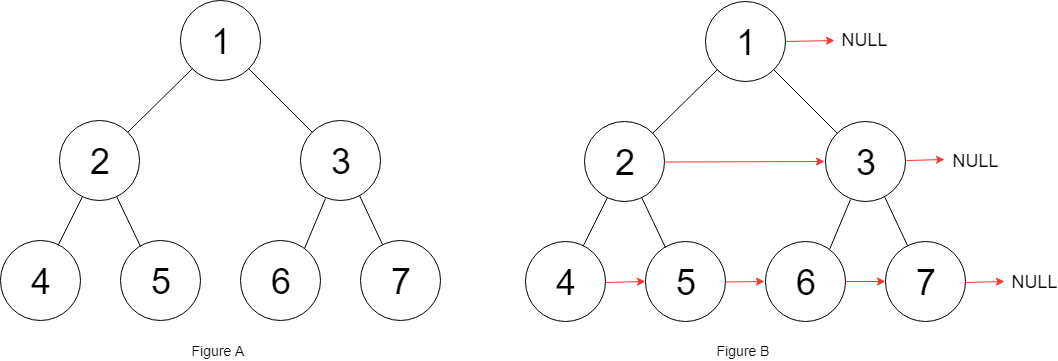
输入：root = [1,2,3,4,5,6,7] 输出：[1,#,2,3,#,4,5,6,7,#] 解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，’#’ 标志着每一层的结束。

✨ 解题：

其实要解这个题，关键在于要知道怎么样对二叉树进行层序遍历，也就是一层一层的把二叉树中的所有元素遍历出来。而要实现这种层次的遍历，不难想到使用队列。
对于这个题来说，观察可知，如果当前节点不等于这一层的最后一个节点，其 next 就要指向这一层的下一个节点，而下一个节点实际就是队列中的下一个元素（因为左孩子会比右孩子先进入队列），因此最后的代码实现如下：

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;
    Node() : val(0), left(NULL), right(NULL), next(NULL) {}
    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
    Node* connect(Node* root) {
        if(root == NULL){
            return NULL;
        }
        queue<Node*> q;
        q.push(root); // 二叉树的根节点入队
        while(!q.empty()){  // 队列不为空的时候
            int sum = q.size();  // q.size()就是当前层次中的节点数目
            for(int i = 0;i < sum;i++){
                Node* node = q.front(); 
                q.pop();
                if(i < sum-1){ // 如果不是最后一个元素
                    node->next = q.front();
                }
                if(node->left != NULL){ // 把下一层的元素添加到队列中
                    q.push(node->left);
                }
                if(node->right != NULL){
                    q.push(node->right);
                }
            }
        }
        return root;
    }
};