✨题目

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。

✨样例

样例1

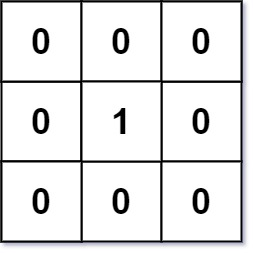
输入：mat = [[0,0,0],[0,1,0],[0,0,0]] 输出：[[0,0,0],[0,1,0],[0,0,0]]

样例2

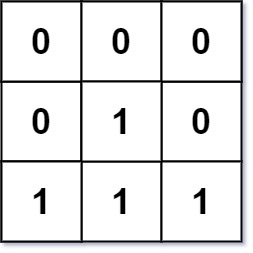
输入：mat = [[0,0,0],[0,1,0],[1,1,1]] 输出：[[0,0,0],[0,1,0],[1,2,1]]

✨提示

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• mat 中至少有一个 0

✨解题：

分析：

这个题题面的意思大概就是要找到矩阵中所有的 1 到最近的 0 的距离。不妨翻转一下，从矩阵中的 0 开始，找到一步拓展能找到的所有的 1 ，那么这些 1 对应的最短距离应该就是 1，然后利用这些得到的 1，继续去拓展其他的点，每次的距离等于上一次的距离+1

AC代码：

class Solution {
public:
    int _next[4][2] = {{1,0},{-1,0},{0,-1},{0,1}};
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        int m = mat.size();
        int n = mat[0].size();
        vector<vector<int>> dis(m,vector<int>(n));
        vector<vector<bool>> book(m,vector<bool>(n));
        queue<pair<int,int>> q;
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                if(mat[i][j] == 0){
                    q.push(make_pair(i,j)); // 把所有的超级源点加入到队列中
                    book[i][j] = true;  // 标记为访问过
                }
            }
        }
        while(!q.empty()){
            pair<int,int> p = q.front();
            q.pop();
            for(int i = 0;i < 4;i++){
                int next_x = p.first + _next[i][0];
                int next_y = p.second + _next[i][1];
                if(next_x < 0 || next_y < 0 || next_x >= m || next_y >= n){
                    continue;
                }
                if(!book[next_x][next_y]){
                    dis[next_x][next_y] = dis[p.first][p.second] + 1;
                    q.push(make_pair(next_x,next_y));
                    book[next_x][next_y] = true;
                }
            }
        }
        return dis;
    }
};