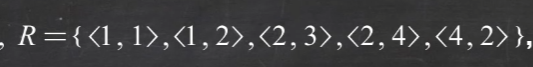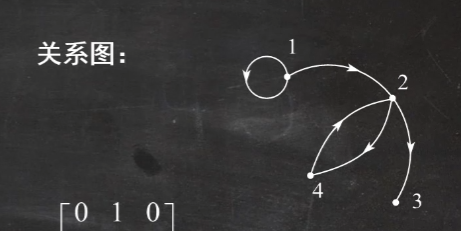一、有序对与笛卡尔积

1、有序对

定义：由两个元素 x 和 y 按照一定的顺序排列而成的二元组，记作<x,y>

2、笛卡尔积

image.png

例题：求两个集合的笛卡尔积

不难发现笛卡尔积运算不满足交换律
image.png

笛卡尔积的性质

image.png

二、二元关系

二元关系的前提条件：
如果一个集合满足下面的条件之一：

  1. 集合是非空集合，且其中的每个元素都是有序对
  2. 集合是空集

就称该集合是一个二元关系，记作R。对于二元关系R，如果<x,y>∈R，那么记作xRy
image.png

集合的特殊关系

空关系： 空集
全域关系：集合和自身的笛卡尔积组成全域关系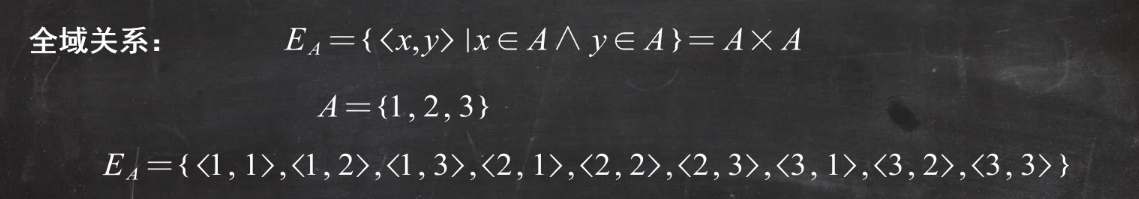
image.png
恒等关系：第一个元素和第二个元素是相同的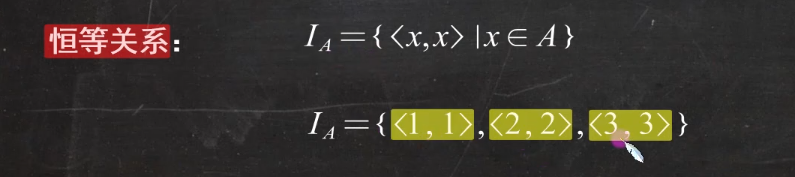
image.png

二元关系的表示方法

表示一个二元关系的方法有3种：集合表达式，关系矩阵和关系图

  1. 集合表达式 用有序对的方式进行表示
    image.png
  2. 关系矩阵 使用一个二维的矩阵进行表示
    image.png
  3. 关系图 使用有向线段构成的图进行表示
    image.png

    例题：根据关系矩阵还原二元关系

    image.png


    二元关系的运算

假设🚆七、二元关系 - 图12是一个二元关系

  1. 定义域：🚆七、二元关系 - 图13中所有有序对的第一元素构成的集合，记作🚆七、二元关系 - 图14
  2. 值域：🚆七、二元关系 - 图15中所有有序对的第二元素构成的集合，记作🚆七、二元关系 - 图16
  3. 域：🚆七、二元关系 - 图17的定义域和值域的并集，记作🚆七、二元关系 - 图18

例题：求一个二元关系的定义域、值域和域

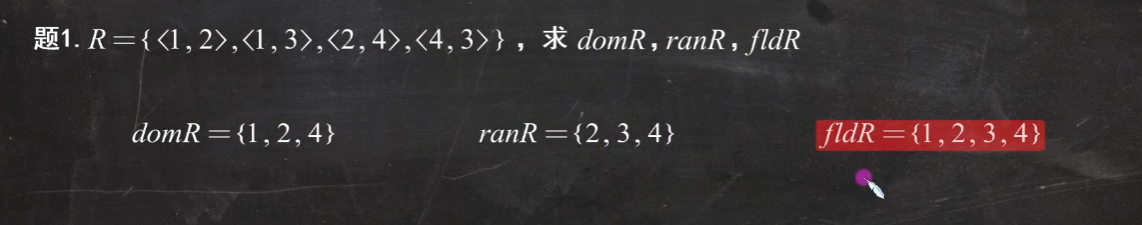
image.png

  1. 逆关系(逆)：🚆七、二元关系 - 图20的逆关系，简称为🚆七、二元关系 - 图21的逆，记作🚆七、二元关系 - 图22
    🚆七、二元关系 - 图23🚆七、二元关系 - 图24
    image.png

    例题：求二元关系的逆关系和右复合

    image.png

    课后练习题

    image.png
    image.png
    image.png

    三、关系的性质

    1、二元关系的性质

    image.png

  2. 自反

  3. 反自反
  4. 对称
  5. 反对称
  6. 传递

image.png

例题：根据集合表达式来判断满足哪些性质

image.png

例题：根据关系图来判断满足哪些性质

image.png

例题：根据关系矩阵来判断满足哪些性质

根据关系矩阵不好判断传递性，一般通过关系矩阵画出关系图，然后通过关系图判断传递性
image.png

2、关系的闭包

image.png

例题：求关系R的自反闭包、对称闭包和传闭包

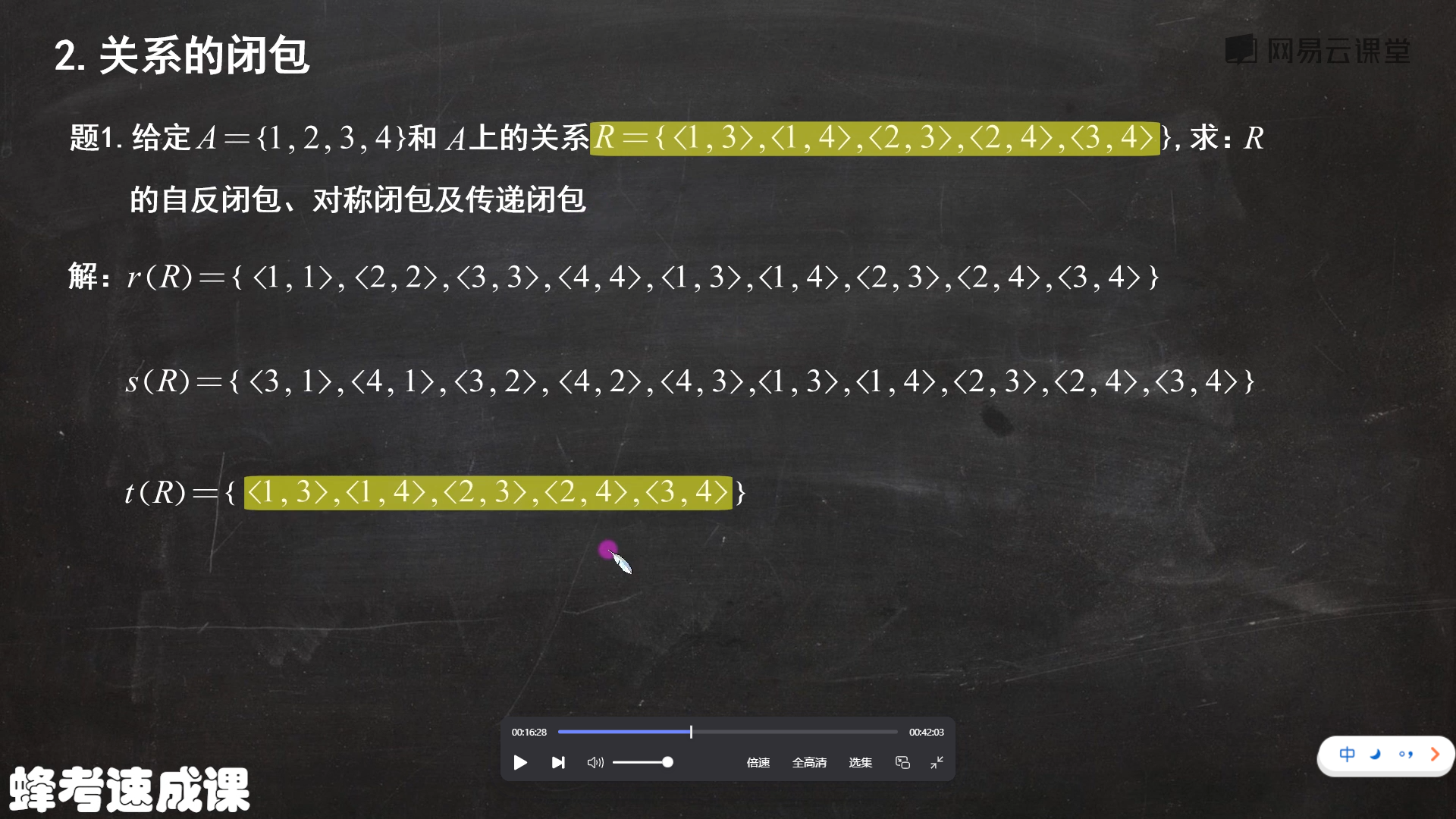
image.png

3、等价关系与划分

3.1 等价关系

image.png

例题：求等价类

image.png

例题：根据一个二元关系证明另外一个二元关系

🚆七、二元关系 - 图39

  1. 证明自反性
    1. 🚆七、二元关系 - 图40
  2. 证明对称性
    1. 🚆七、二元关系 - 图41
  3. 证明传递性
    1. 🚆七、二元关系 - 图42

image.png

3.2 划分

image.png

例题：判断给定的子集族🚆七、二元关系 - 图45是否是集合的一个划分

判断依据：

  1. 子集族中不包含空集
  2. 子集族各个子集之间没有相交的部分，交集为 🚆七、二元关系 - 图46
  3. 子集族中，各个子集的并集等于集合A

只有同时满足上述三个条件，子集族🚆七、二元关系 - 图47才是集合A的一个划分
image.png

例题：根据划分求等价关系

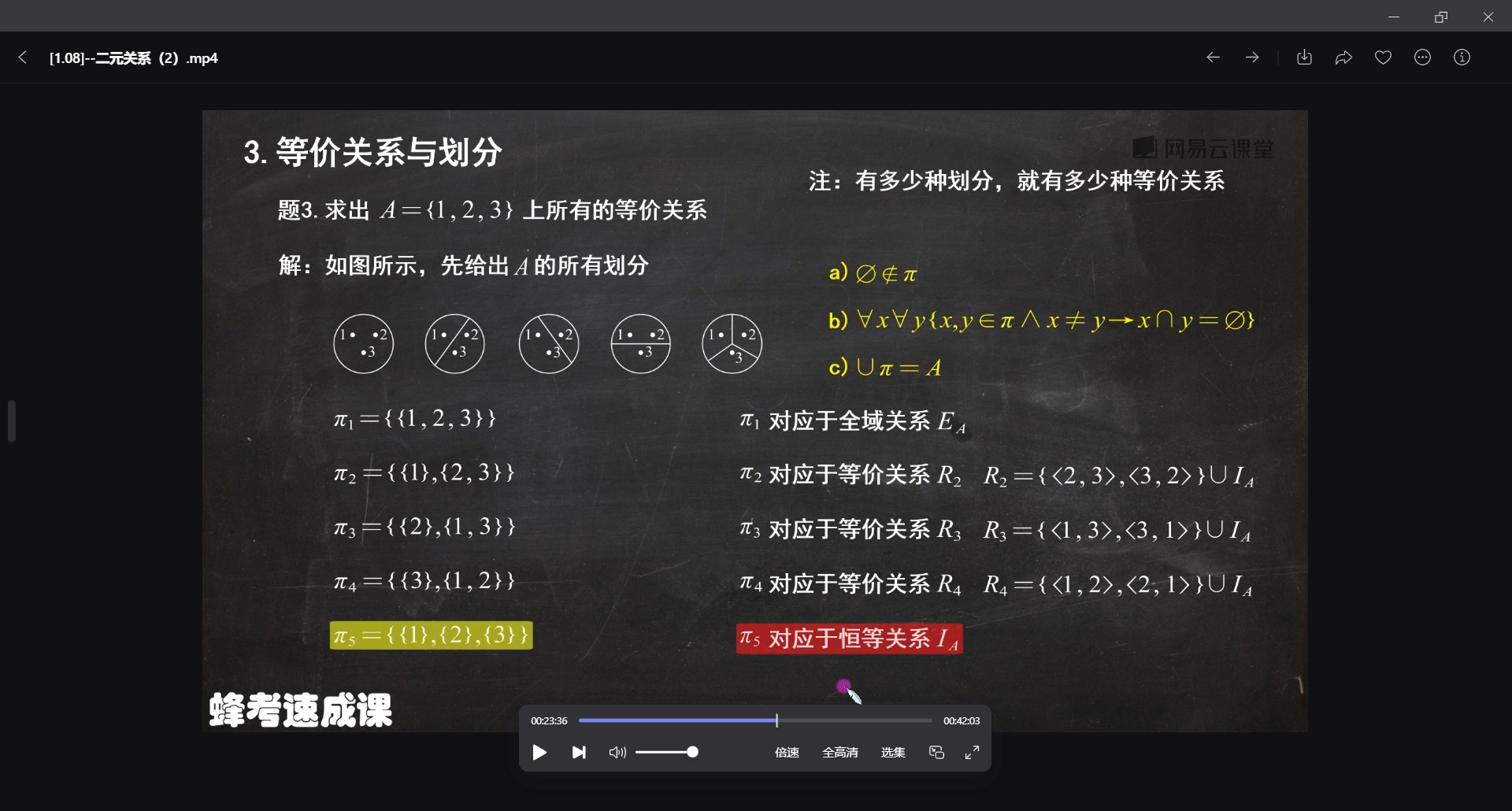
image.png

4、偏序关系

4.1 偏序关系和哈斯图

image.png

例题 ：求偏序集并画出哈斯图

  1. 🚆七、二元关系 - 图51没有整除关系，所以二者处于同一行
  2. 🚆七、二元关系 - 图52
  3. 🚆七、二元关系 - 图53
    🚆七、二元关系 - 图54
  4. 🚆七、二元关系 - 图55
    🚆七、二元关系 - 图56

image.png

4.2 最大元和最小元

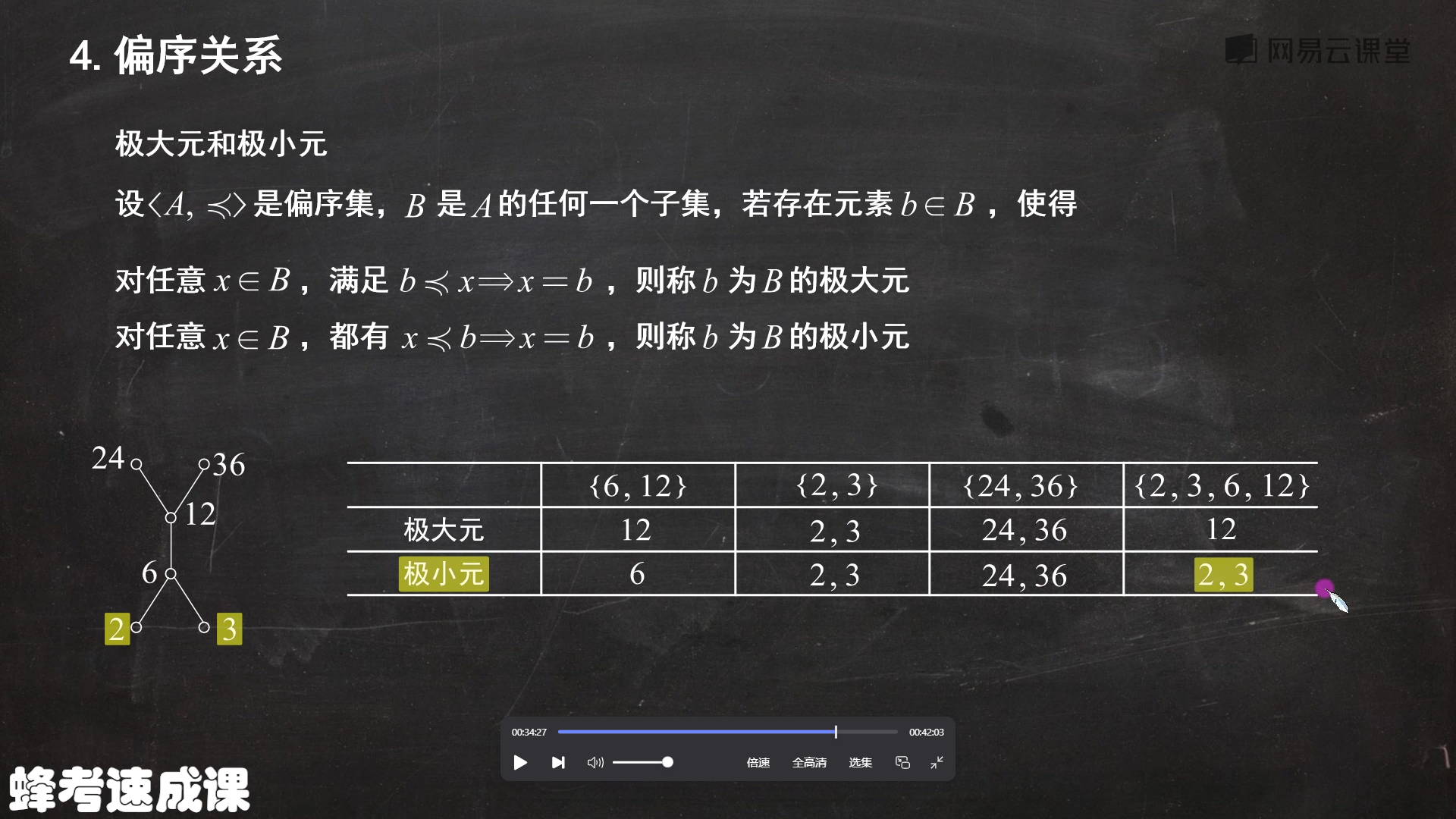
image.png

4.3 极大元和极小元

  1. 找子集中的最大值和最小值
  2. 判断这两个值是否在哈斯图的同一层上
    1. 在同一层上，就两者既是极大元也是极小元（参考下图第二列）
    2. 不在同一层上，那么子集中的最大值就是极大元，最小值就是极小元
  3. 哈斯图中的孤立顶点，既是极小元，也是极大元

image.png

4.4 上界和上确界

上界：对应哈斯图中大于等于子集中极大元层数的所有点
上确界：上界中的最小值

  1. 🚆七、二元关系 - 图60🚆七、二元关系 - 图61
  2. 🚆七、二元关系 - 图62，🚆七、二元关系 - 图63
  3. 🚆七、二元关系 - 图64
  4. 🚆七、二元关系 - 图65

image.png

4.5 下界和下确界

下界：哈斯图中小于等于极小元所在层数的所有点
下确界：下界中的最大值

  1. 🚆七、二元关系 - 图67
  2. 🚆七、二元关系 - 图68
  3. 🚆七、二元关系 - 图69
  4. 🚆七、二元关系 - 图70
  5. 🚆七、二元关系 - 图71
  6. 🚆七、二元关系 - 图72

image.png

课后练习题

image.png
image.png
image.png
image.png
image.png