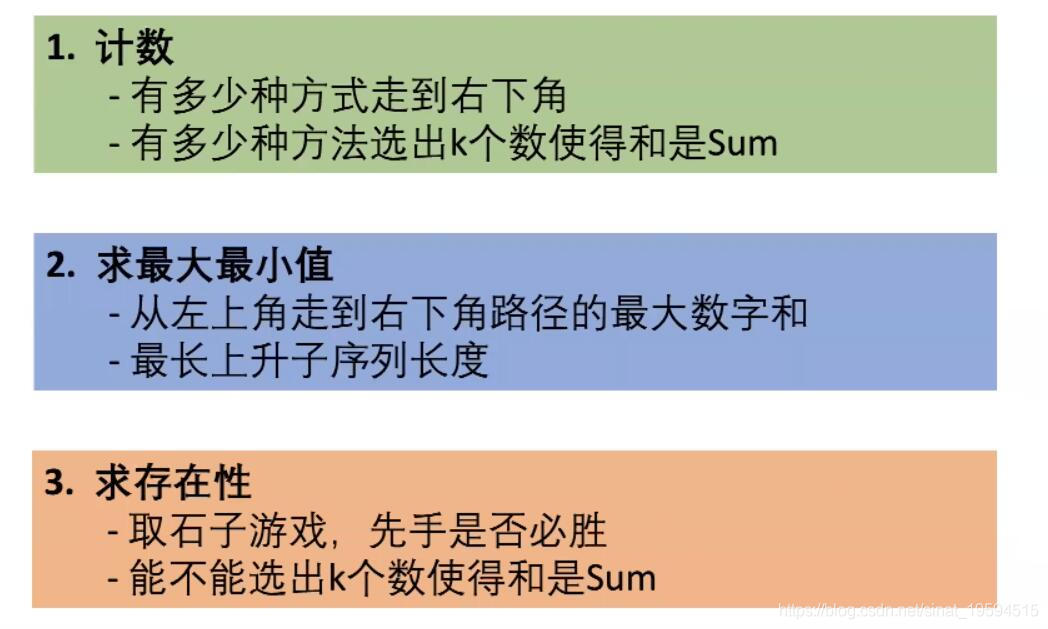
动态规划一般是用来解决以下几类问题：
1、计数
2、求最大值、最小值
3、求事件的存在性

动态规划的一般解题步骤
1、确定状态
· 确定最后一步
· 转化成为一个个子问题
2、写出状态转移方程
3、确定开始和边界的条件
4、计算顺序

说了跟没说一样（也太抽象了）
不如直接做一道题看看

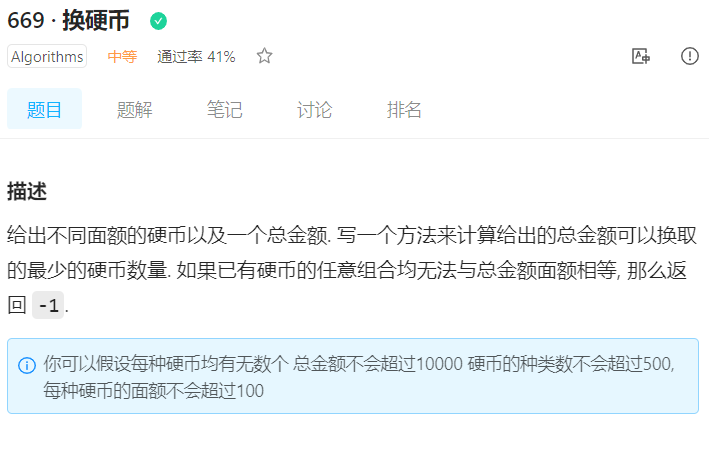
1、LintCode 669 换硬币

1、确定状态

1.1”最后一步”

首先我们把最后一个硬币的面值是ak,那么前面的硬币值肯定是27-ak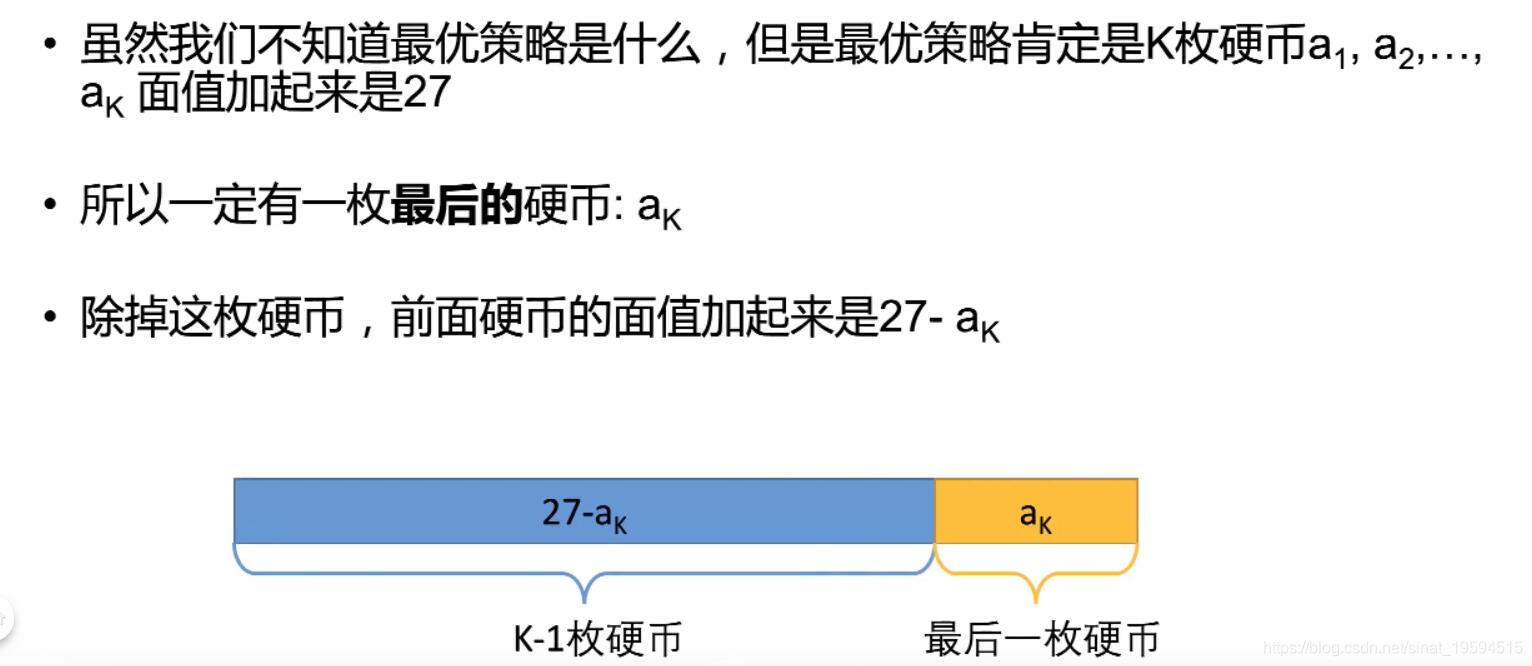

接下下,”最后一步”还有两个注意的关键点

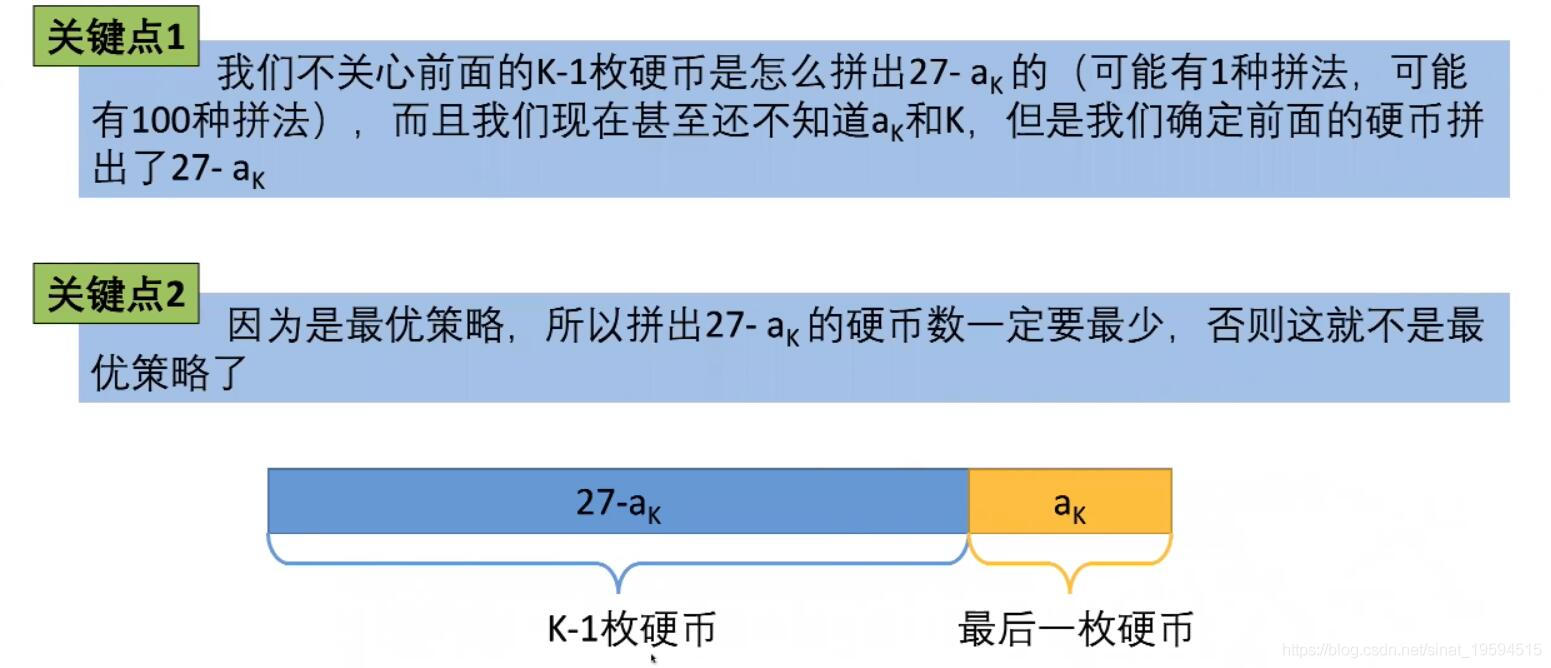
1.2 化解子问题

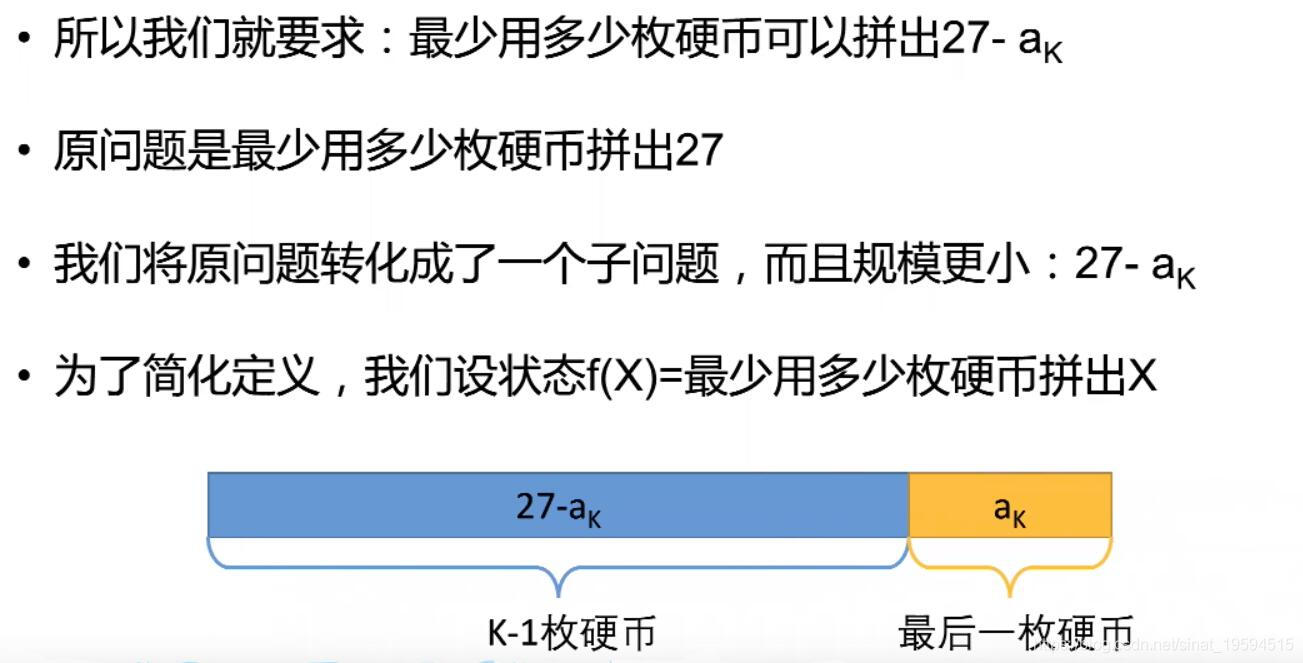
还有个问题,我们还不知ak是多少,所以需要

这样我们的第一步就完成了

2、确定转移方程

根据第一步的状态,我们这样设置,(注意,上面的大括号在这一步已经变成方括号了)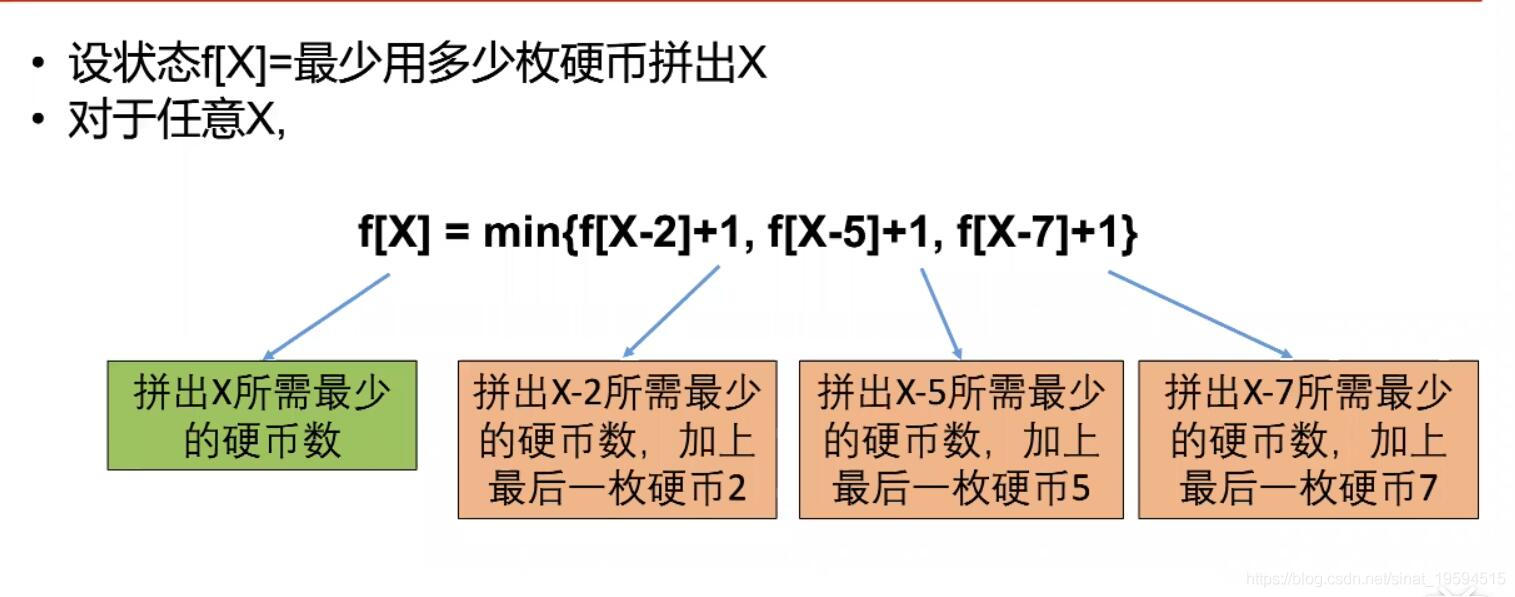

完成这一步可以先喝杯咖啡了

3、确定开始和边界条件

首先我们的硬币肯定从f[0]即凑出0元需要0枚硬币,

接下来是边界问题:

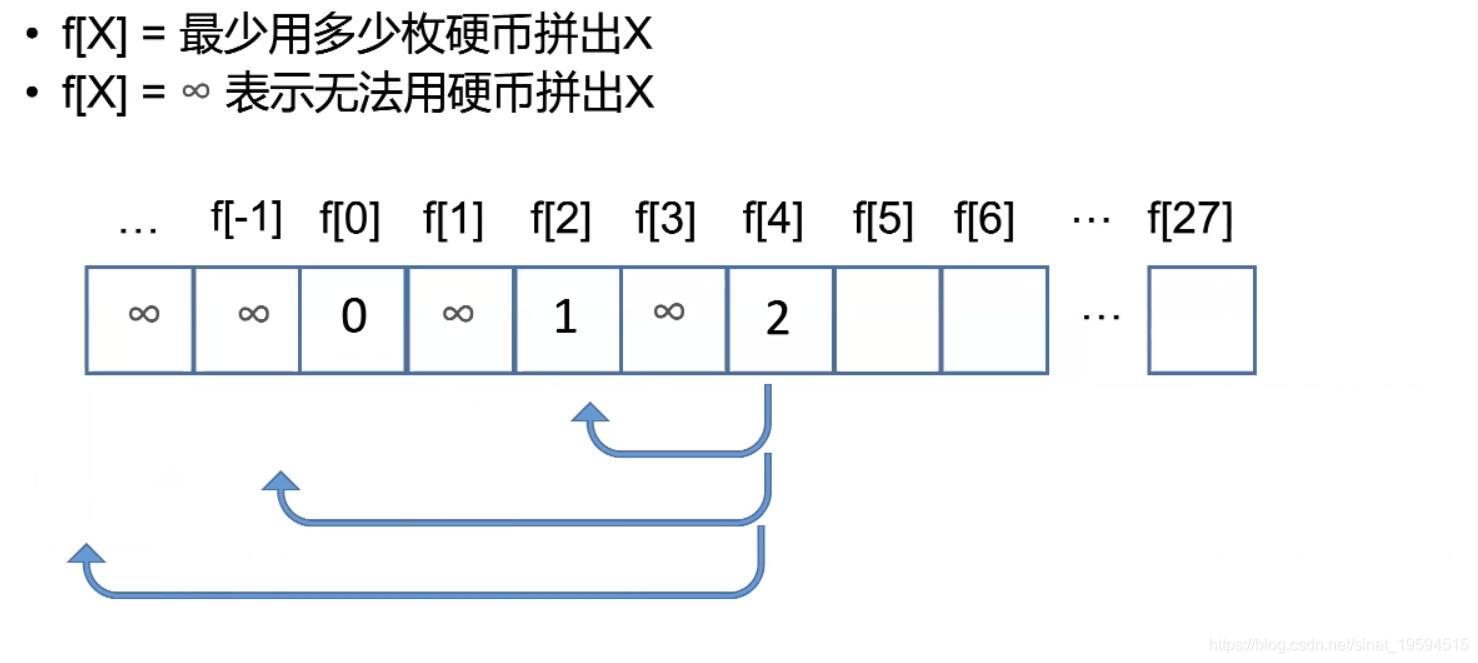
4、计算顺序

有了我们前面分析的前三步,接下来就是计算顺序了,其实就是从f[0]开始计算而已,并把他们都记录下来

结果其实是这样的

5、代码

package test
public class application {
    public static void main(String[] args) {
        int money = 27;  //假设需要拼凑的总金额为27元
        int[] coin = new int[3];  //拥有的硬币面额
        int[] dp = new int[money+1];  // 动态规划用到的数组
        coin[0] = 2;
        coin[1] = 5;
        coin[2] = 7;
        dp[0] = 0;  // 拼凑出0元所需要的硬币数为0
        for(int i = 1;i <= money;i++){
            dp[i] = Integer.MAX_VALUE; //  默认拼凑出i元所需要的硬币数为无穷大（无法拼凑出来）
            for(int j = 0;j < coin.length;j++){
                if(i - coin[j] >= 0 && dp[i-coin[j]] != Integer.MAX_VALUE){
                    dp[i] = Math.min(dp[i],dp[i-coin[j]] + 1);
                }
            }
        }
        if(dp[money] == Integer.MAX_VALUE){
            System.out.println("不能够拼凑出来");
        }
        else{
            System.out.println(dp[money]);
        }
    }
}

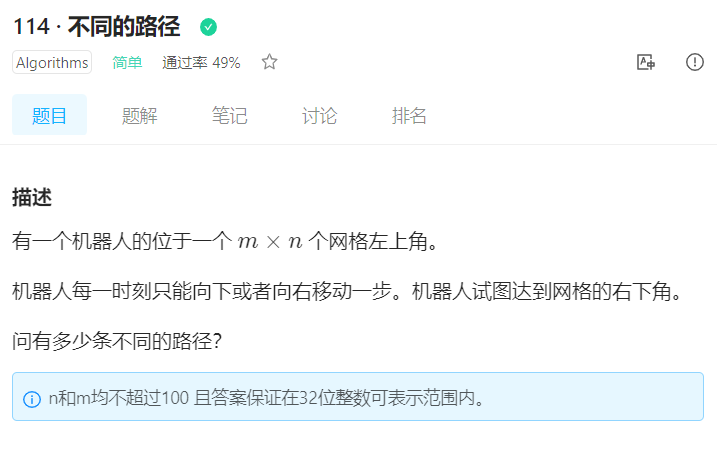
2、LintCode 114 不同的路径

1、确定状态

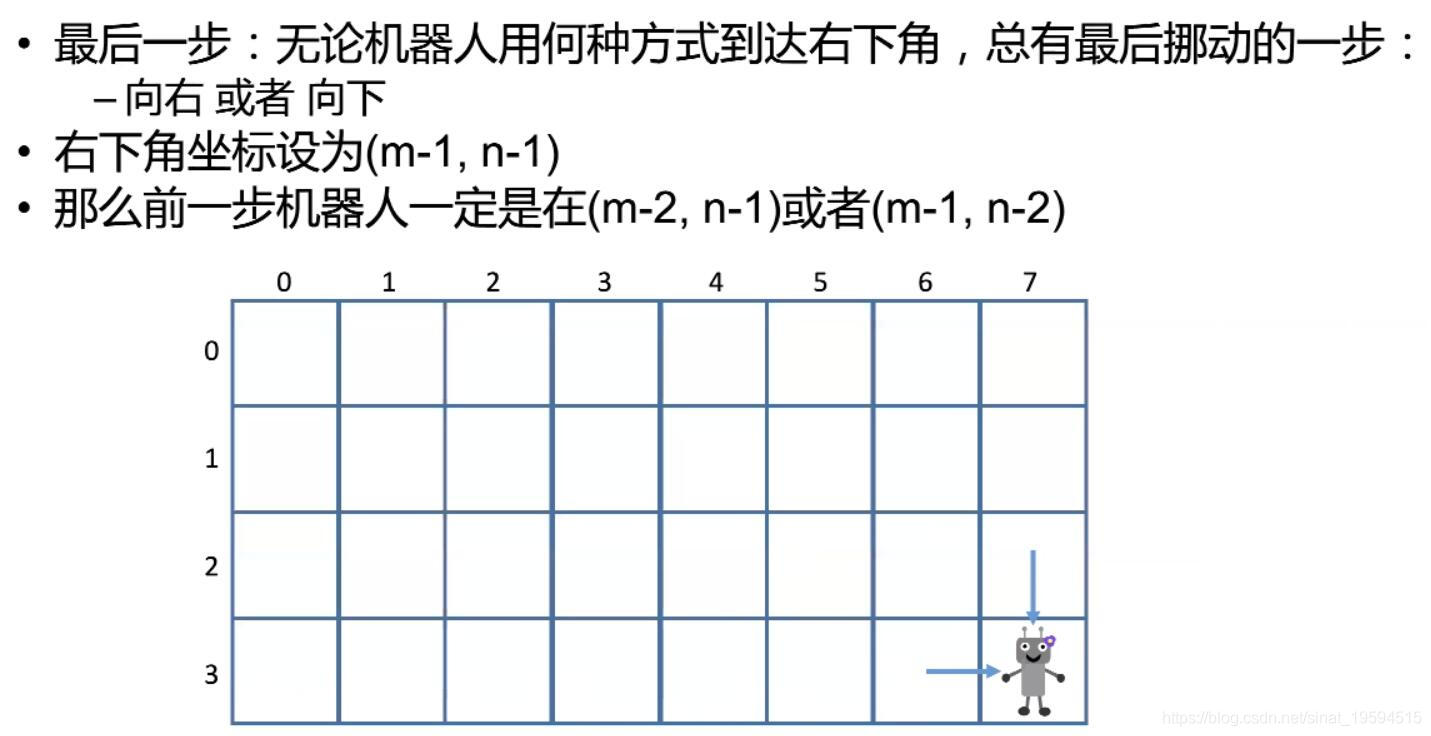
1.1 最后一步

1.2 化解子问题

2、状态转移方程

设F[i][j] 表示到 (i,j) 时方法数，那么，
状态转移方程：

F[i][j] = F[i-1][j] + F[i][j-1]

3、确定开始和边界条件

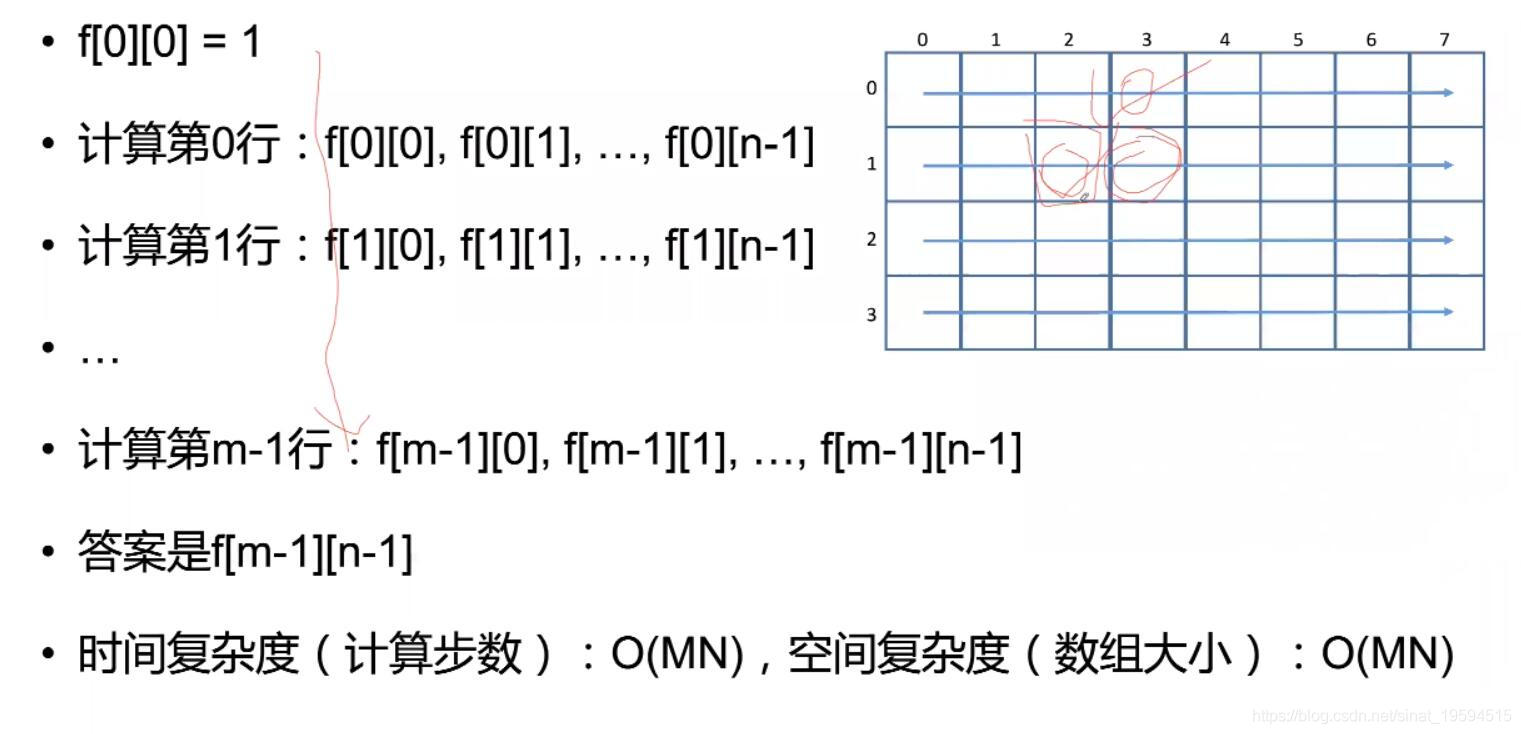
开始：F[0][0] = 1，规定到初始点的方法数只有一种
边界：

  - 当 i = 0 的时候，对应地图中的第0行，由于只能向下或者向右移动，那么到达第0行的任意一列的方法数应该都只有一种。
  - 同理，当 j = 0 的时候，对应地图中的第0列，到达第0列的任意一行的方法数应该都只有一种。

即：

F[0][j] = 1 F[i][0] = 1

4、计算顺序

5、代码

package test2;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
import java.util.Stack;
public class application {
    public static void main(String[] args) {
        int m = 3;
        int n = 3;
        int [][]dp = new int[m+1][n+1];
        dp[0][0] = 1;
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                if(i == 0 || j == 0){
                    dp[i][j] = 1;
                }
                else {
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                }
            }
        }
        System.out.println(dp[m-1][n-1]);
    }
}

3、LintCode 115 不同的路径Ⅱ

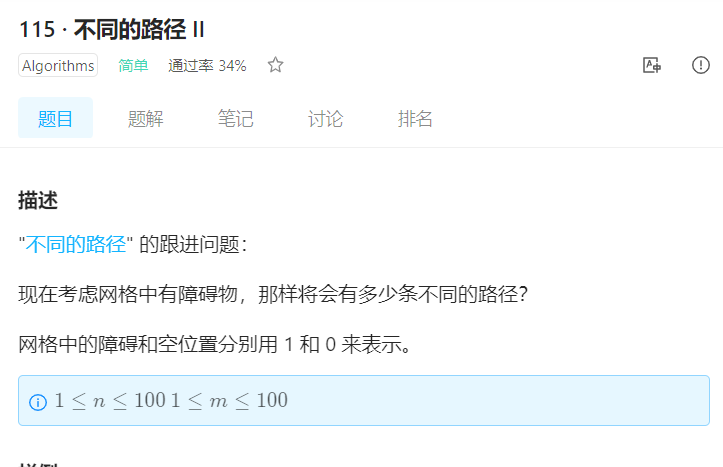
public class Solution {
    /**
     * @param obstacleGrid: A list of lists of integers
     * @return: An integer
     */
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        // write your code here
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][]dp = new int[m+1][n+1]; 
        dp[0][0] = 1;
        if(obstacleGrid[0][0] == 1)
            return 0;
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                if((i == 0 || j == 0) && obstacleGrid[i][j] != 1){
                    dp[i][j] = 1;
                }
                if(obstacleGrid[i][j] == 1){
                    dp[i][j] = 0;
                }
            }
        }
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                if(i == 0 && obstacleGrid[i][j] == 1){
                    for(int k = j;k < n;k++){
                        dp[i][k] = 0;
                    }
                    break;
                }
                if(j == 0 && obstacleGrid[i][j] == 1){
                    for(int k = i;k < m;k++){
                        dp[k][j] = 0;
                    }
                }
            }
        }
        for(int i = 1;i < m;i++){
            for(int j = 1;j < n;j++){
                if(obstacleGrid[i][j] == 0)
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}