回归问题是监督学习中的一种，主要用于处理对连续变量的预测问题
    在回归问题中，我们尝试找到一个数学函数（直线或者曲线）来尽量对已有的数据集进行拟合
    这个数学函数也被称为假设函数

    得到了合适的假设函数之后，我们便可以对未知的数据进行预测

    那么如何得到最合适的假设函数？
    以直线拟合为例，假设我们的假设函数如下所示：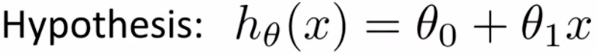
    image.png
    此时，我们并不知道有关θ0和θ1的取值情况
    换句话说，我们就是要选择，最合适的θ0和θ1，从而使直线的拟合情况最好

    那么如何选择最合适的θ0和θ1？
    而要让直线的拟合情况越好，换句话来说，对于数据集中给定的每一个样本数据，我们要让平均误差最小

    而对于给定的数据x，所有数据的平均误差与θ0和θ1相关，因此我们可以使用一个函数，来描述平均误差
    也就是：代价函数
    在直线型回归分析中，我们最常使用平方误差代价函数

    对上述假设函数进行简化，如下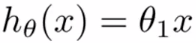：image.png

    对每一个样本点，偏低程度有上、下之分
    因此，我们使用偏移量的平方作为误差的标准，得到如下误差函数：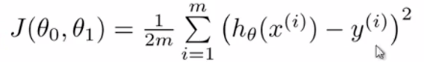
    image.png

    通过对θ1的多次取值，我们可以得到误差函数的图像：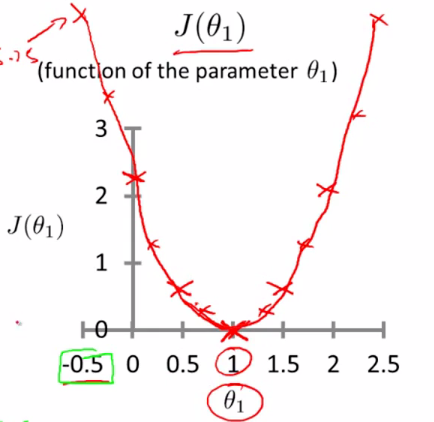
    image.png
    当代价函数取最小值的时候，对应的θ1的值，就可以用来确定我们的假设函数，从而用于后续对未知数据的预测

    而假如我们现在不对假设函数进行简化，使用原始式子：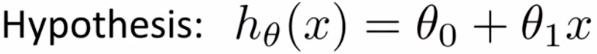
    image.png
    那么，得到的代价函数中，就会同时与θ0和θ1相关，对应的函数图像也不再是二维，而是三位立体图形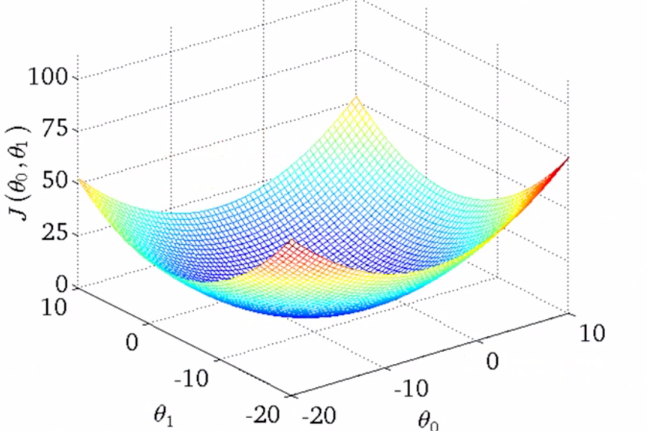
    image.png
    在此图像中，高度对应的就是代价函数的值

    当参数进一步增加，对图形进行可视化的难度也会进一步加大，甚至无法进行可视化操作。