一、连续、偏导存在、全微分存在之间的关系

• 函数连续和偏导存在之间没有任何关系，连续推不出偏导存在，偏导存在推不出连续。
• 偏导存在推不出全微分存在，全微分存在可以推出偏导存在。
• 如果偏导存在且连续，那么可以推出全微分存在。
• 全微分存在可以推出偏导存在，也可以推出函数连续。

二、偏导数的计算

要点：求谁的偏导数就把其他的变量当作常数。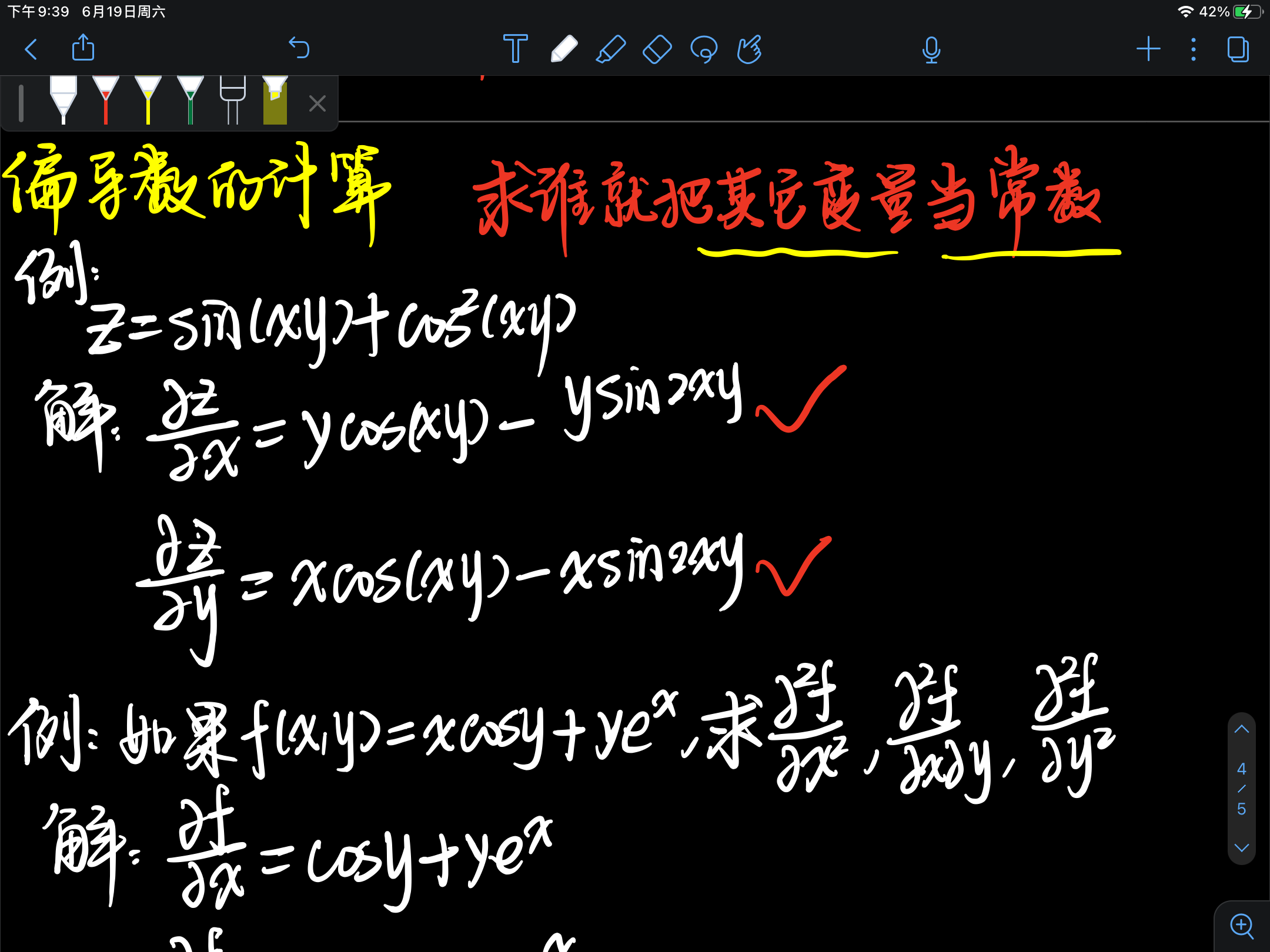

三、全微分的计算

要点：求偏导数，注意不要忘记加上dx，dy，dz
步骤：

• 先求各个变量的偏导数
• 然后按照格式计算全微分

如果是求某一个点的全微分，那么就先计算出全微分，然后代入该点的坐标，注意最后的答案中不要忘了写dx, dy, dz…

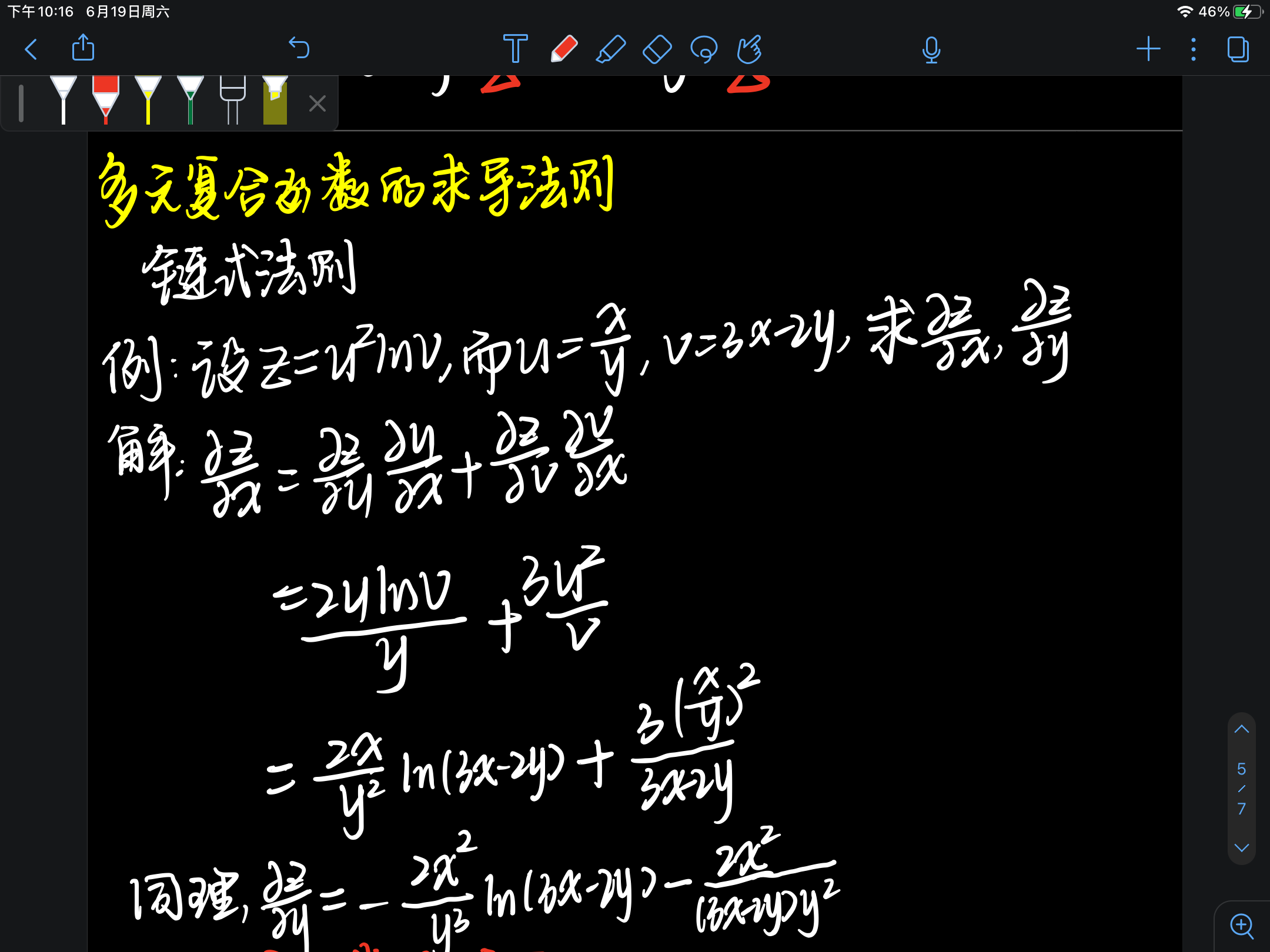
四、复合函数的链式求导法则

注意：

• 1、分清楚每个变量是从哪一个中间变量或者哪几个中间变量来的。
• 2、不要漏了或者重复计算了。

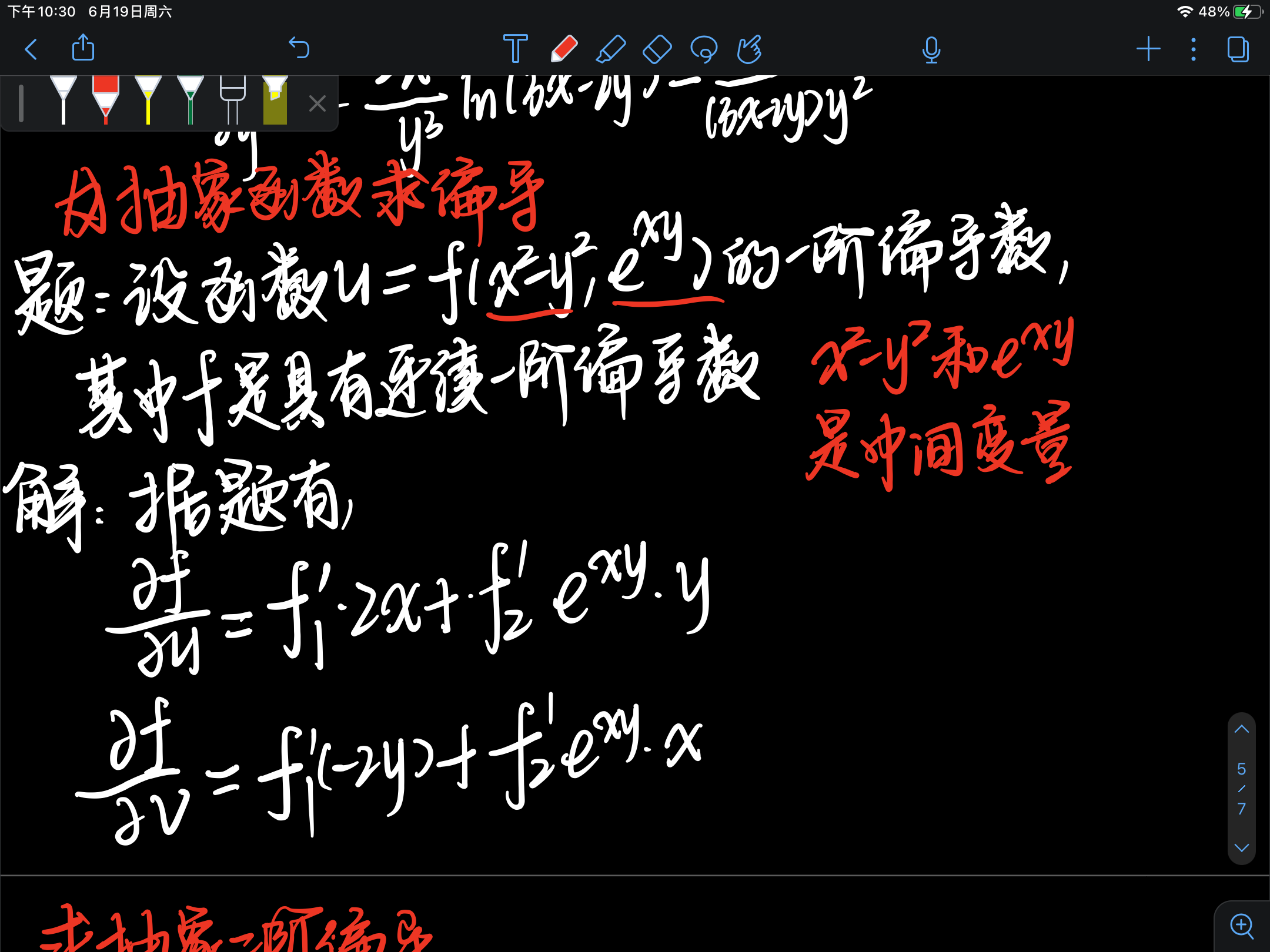
五、抽象函数的链式求导法则

注意：

• 先求一阶偏导数，然后再求二阶偏导数
• 注意二阶偏导数连续的条件，可以减少计算量

**

• 如果 z = f(u,v)，那么 f1 和 f2 都是 (u,v)的函数。
• 求混合二阶偏导数的时候注意是否是乘积求导。

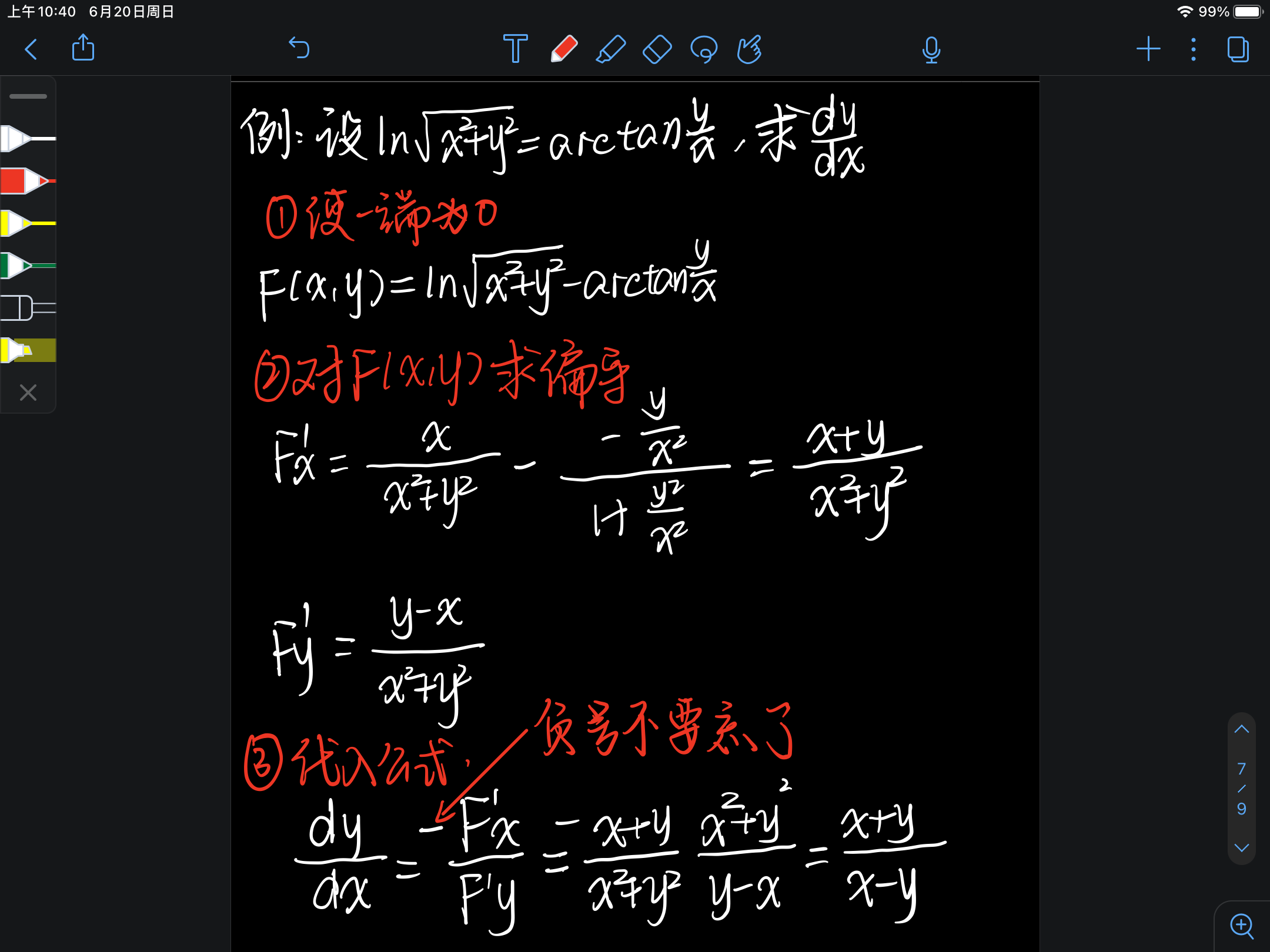
六、隐函数的求导法则

• 二元隐函数的求导

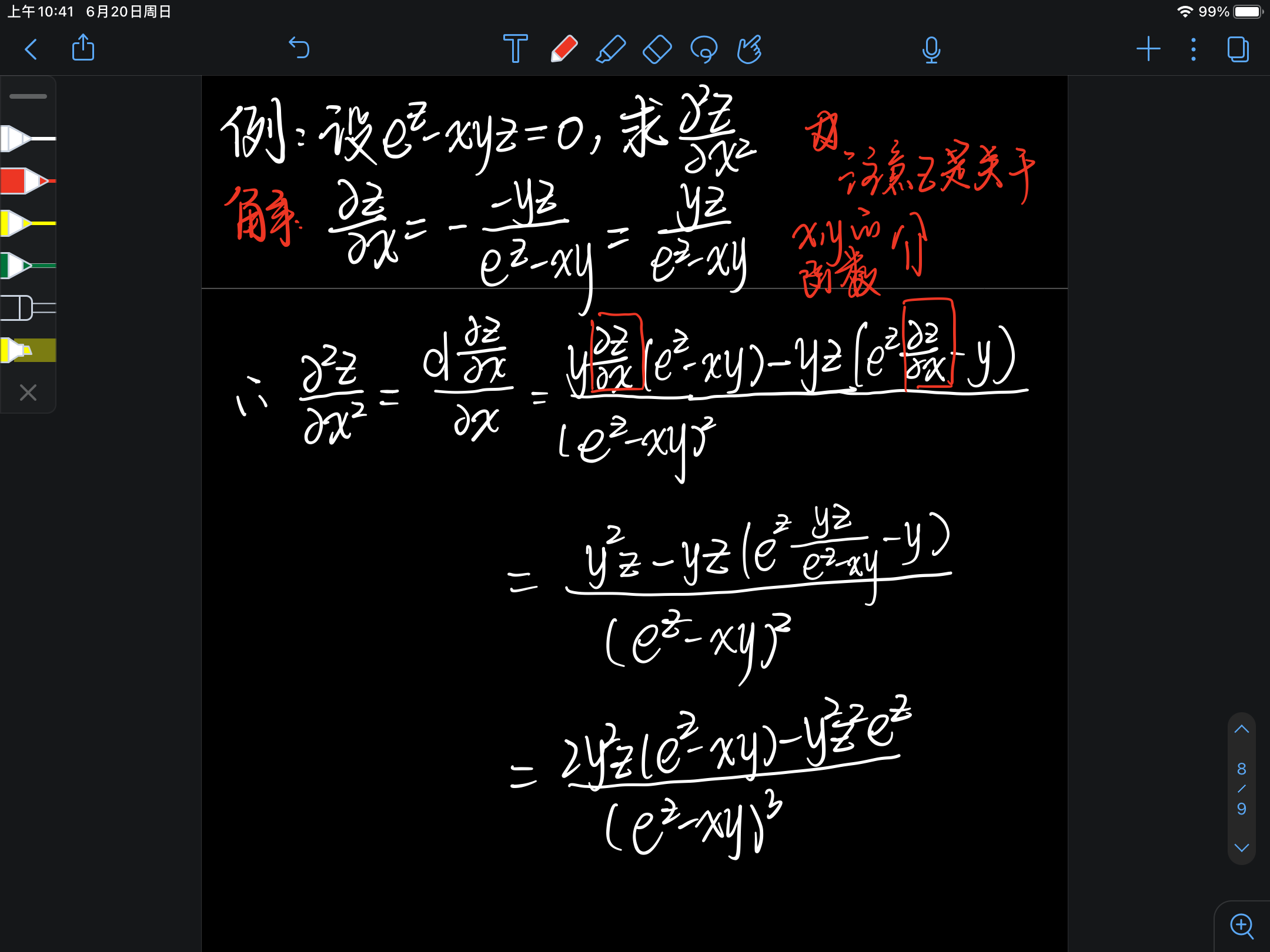
• 三元隐函数的求导
  • 先用隐函数求导法则求出一阶偏导数
  • 再用复合函数求导法则求出二阶偏导数

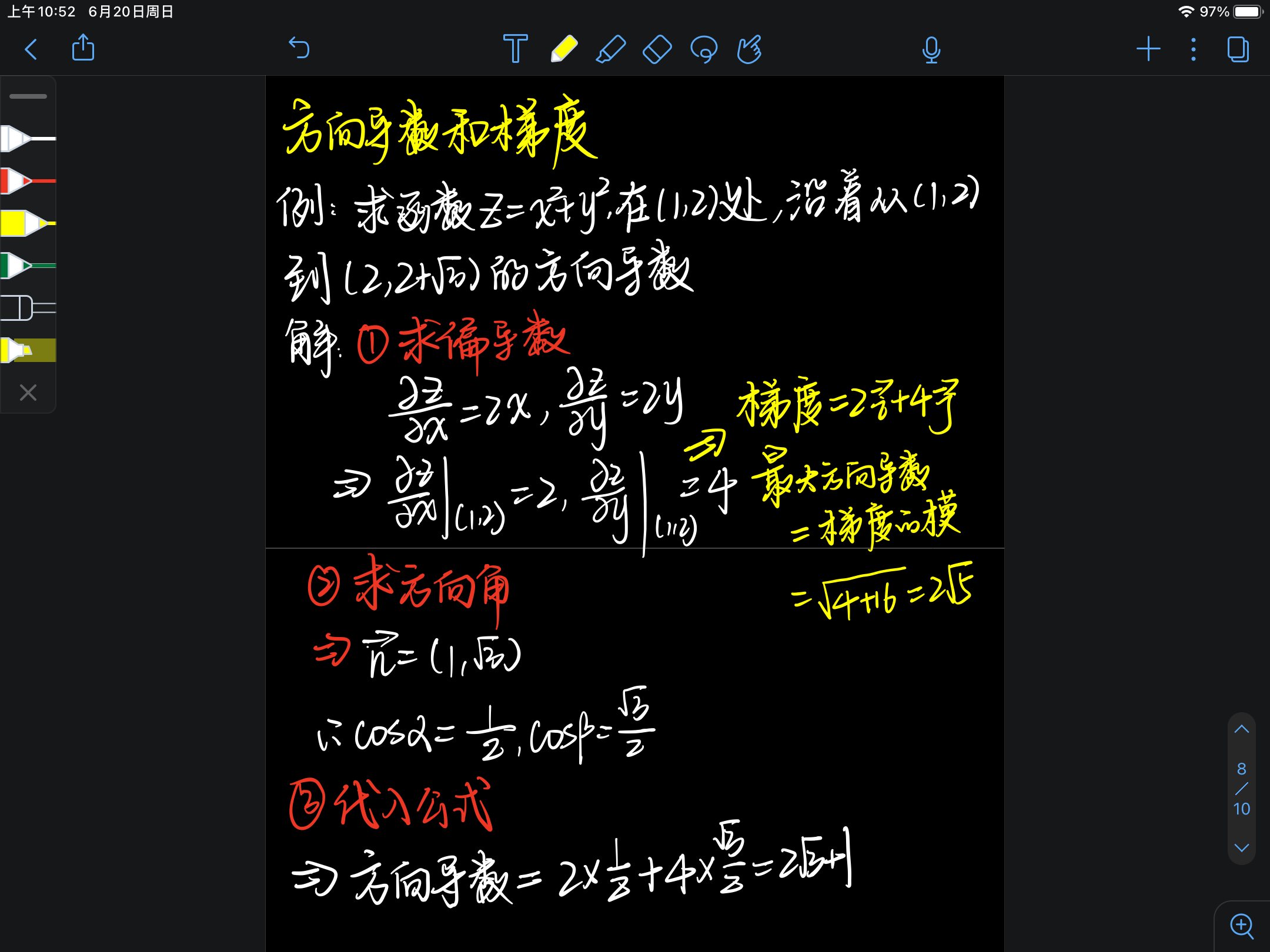
七、方向导数和梯度

• 方向导数：某一点的方向导数等于该点的偏导数乘以对应方向角的和。
• 梯度：等于偏导数乘以对应分量形成的向量。
• 最大方向导数：梯度的模长

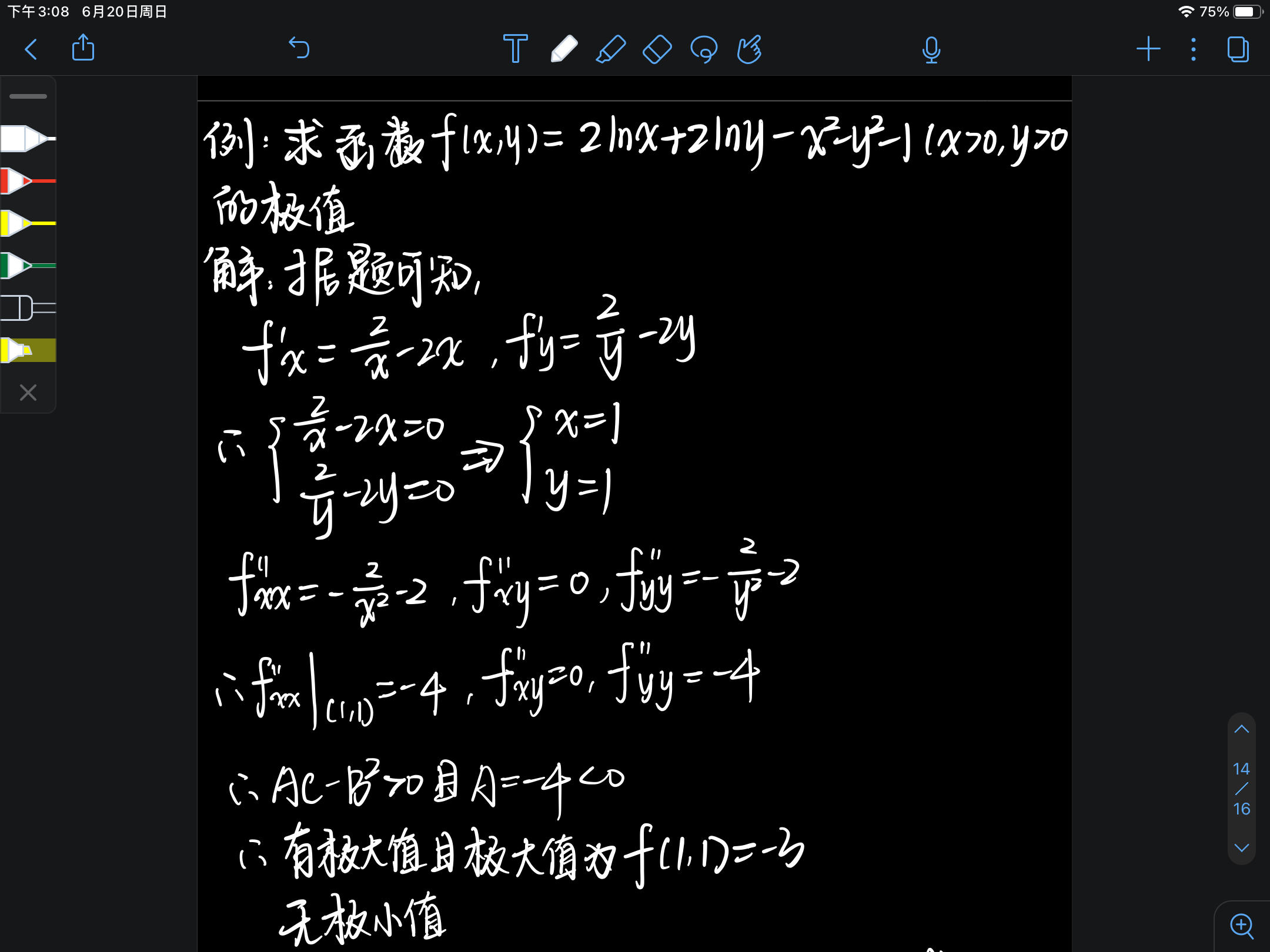
八、多元函数求极值

• 无条件求极值

注意记忆判断是否有极值和是极大值还是极小值的公式

• 有条件求极值 （拉格朗日乘数法）

注意如何构造拉格朗日函数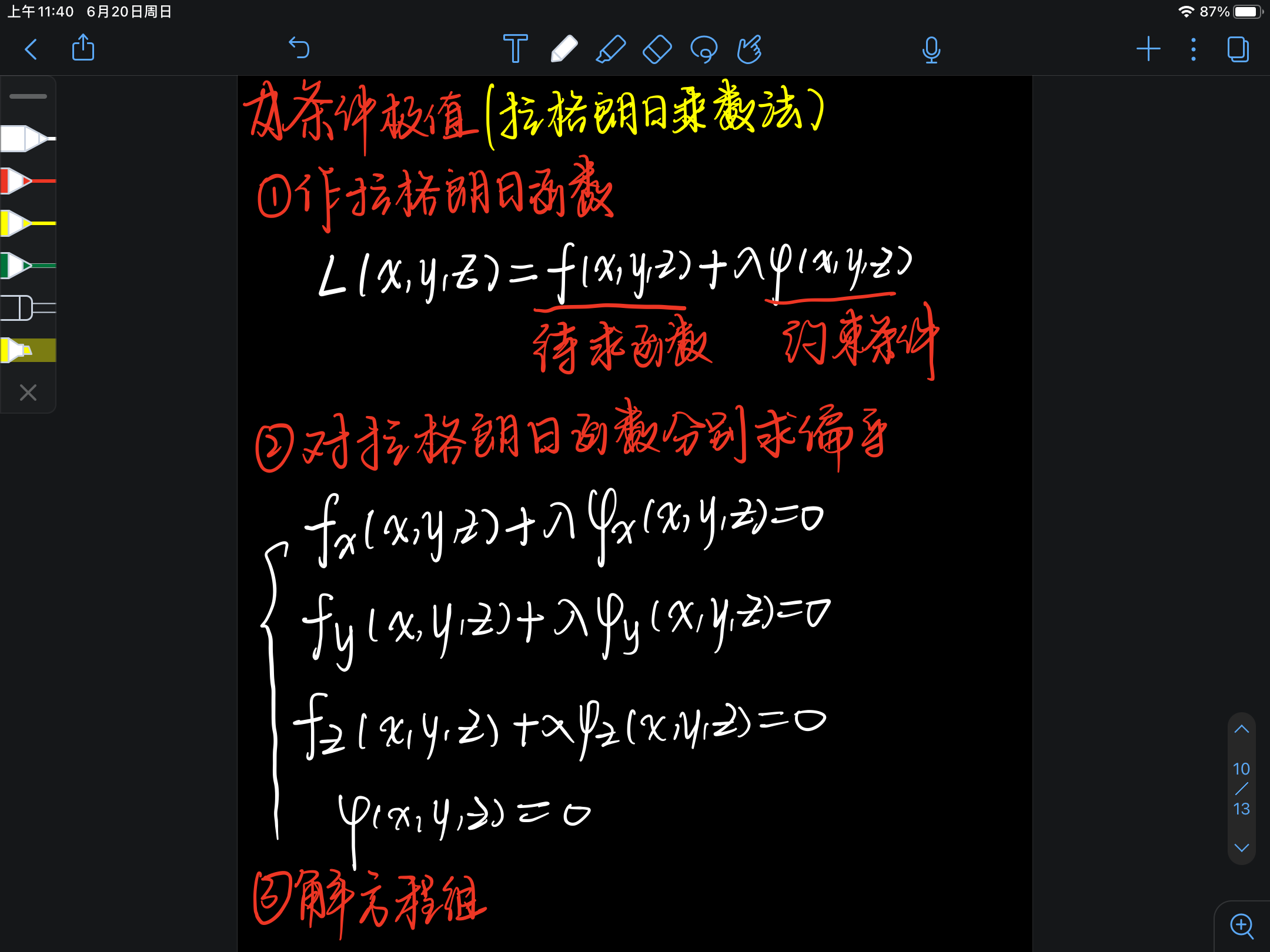

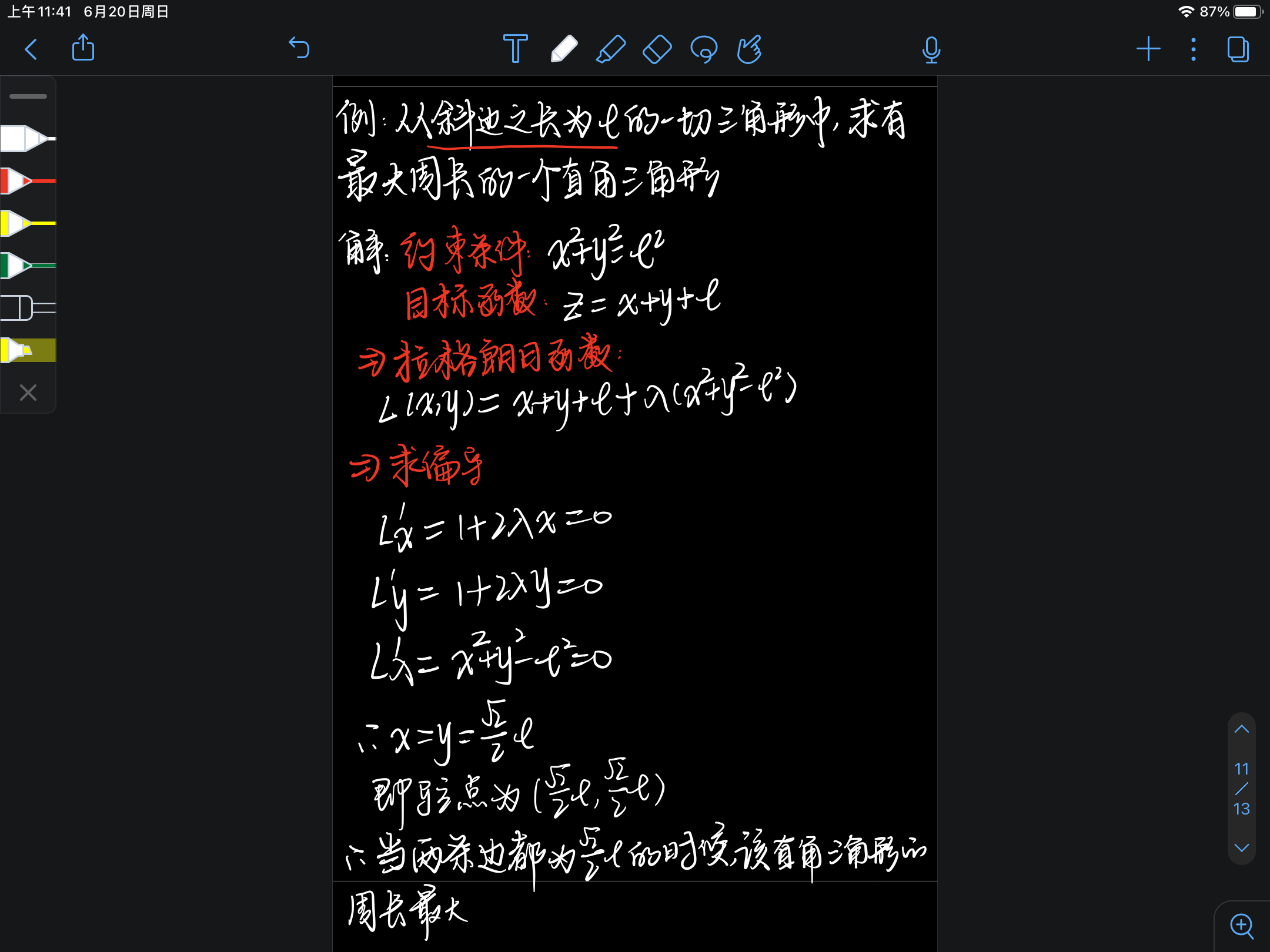
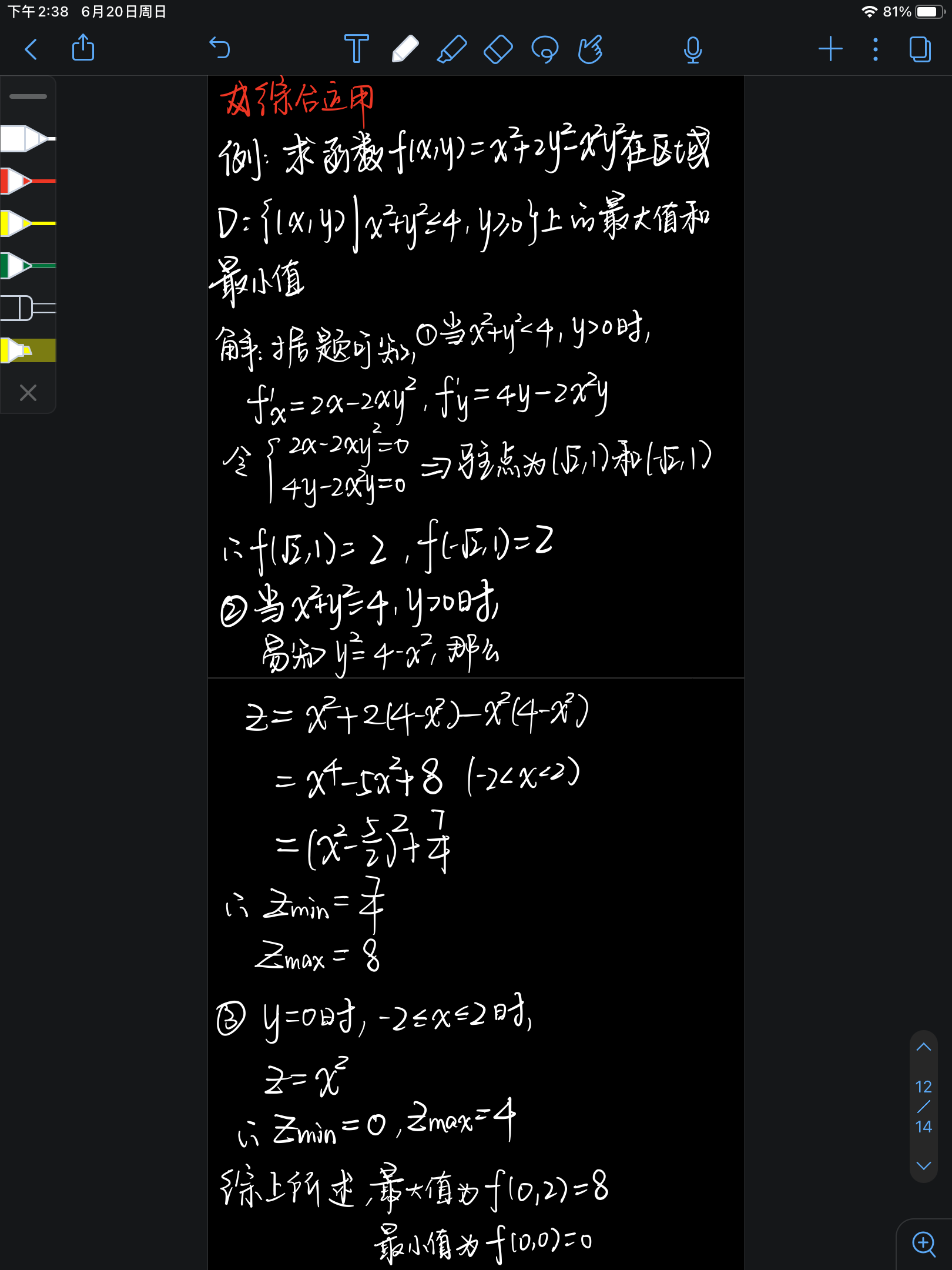
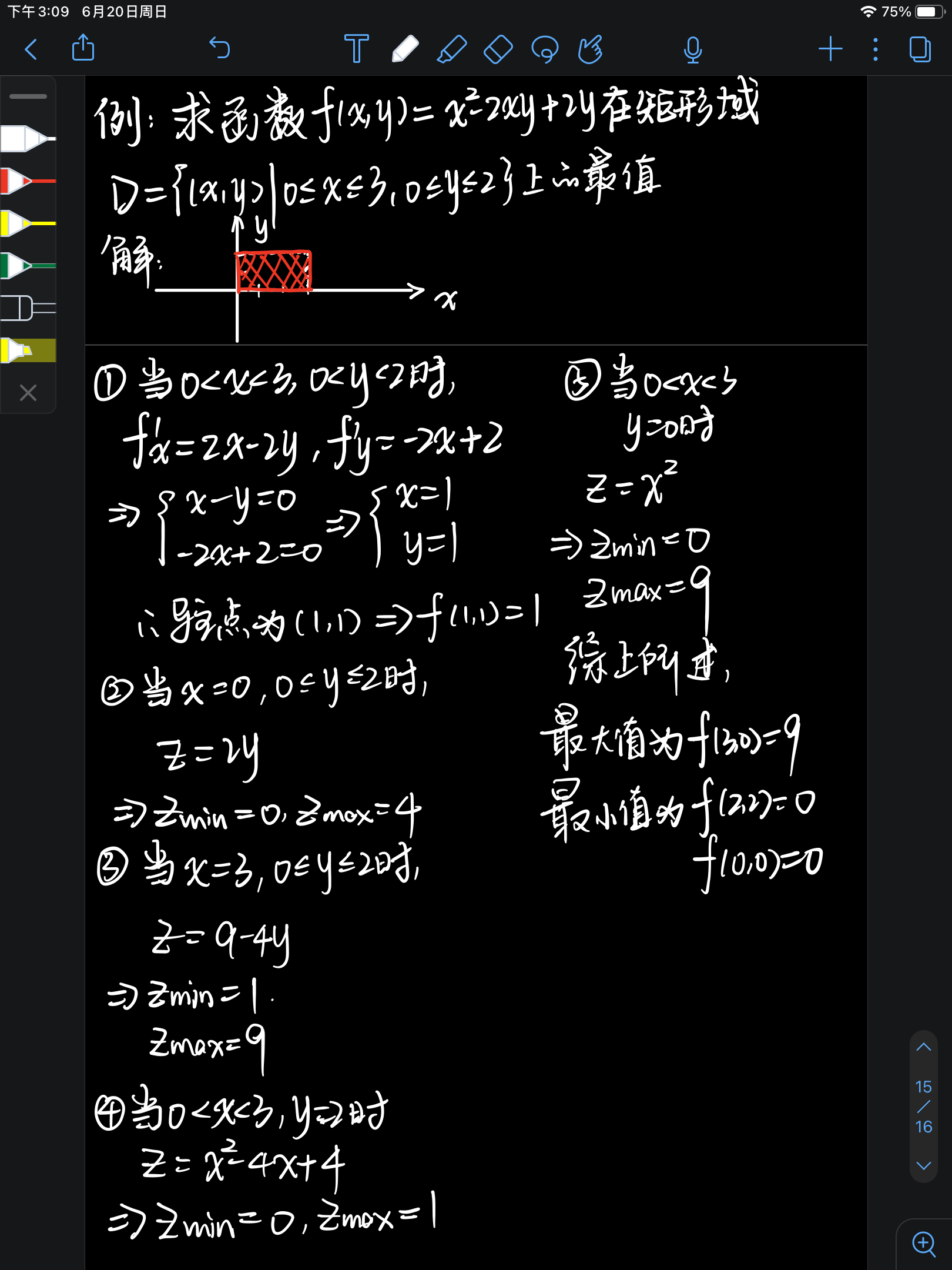
• 有条件极值和无条件极值的综合运用