1、创建集合

创建集合的方法：**

• 直接赋值法

将集合中的元素用花括号包裹起来

arr = {1,2,3,4}
print(type(arr))

• set函数创建法

  • 1、set函数创建空集合

    arr = set()

  • 2、以列表，通过set函数创建集合

    li = [1,1,2,3,4]
    arr = set(li)  # 把列表作为set函数的参数
    print(arr)

    注意集合会自动去重

  • 3、frozenset函数创建法

    li = [1,1,2,3,4]
    arr = frozenset(li)
    print(arr)

    frozenset创建出来的集合是不可以修改的集合
    

2、内存空间

3、input返回值类型默认是字符串

如果要从键盘中输入一个整数并赋给变量x，需要进行 类型转换 ：

x = int(input("请输入变量x的值："))

4、辗转相除法

def gcd(m, n):  # 最大公约数
    if m < n:
        m, n = n, m
    if m % n == 0:
        return n
    else:
        return gcd(n, m % n)  # 函数的递归调用
n = gcd(2, 3)
print(n)

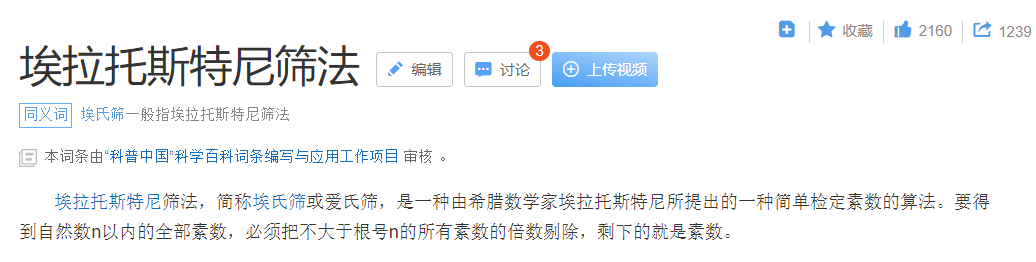
5、埃氏筛法

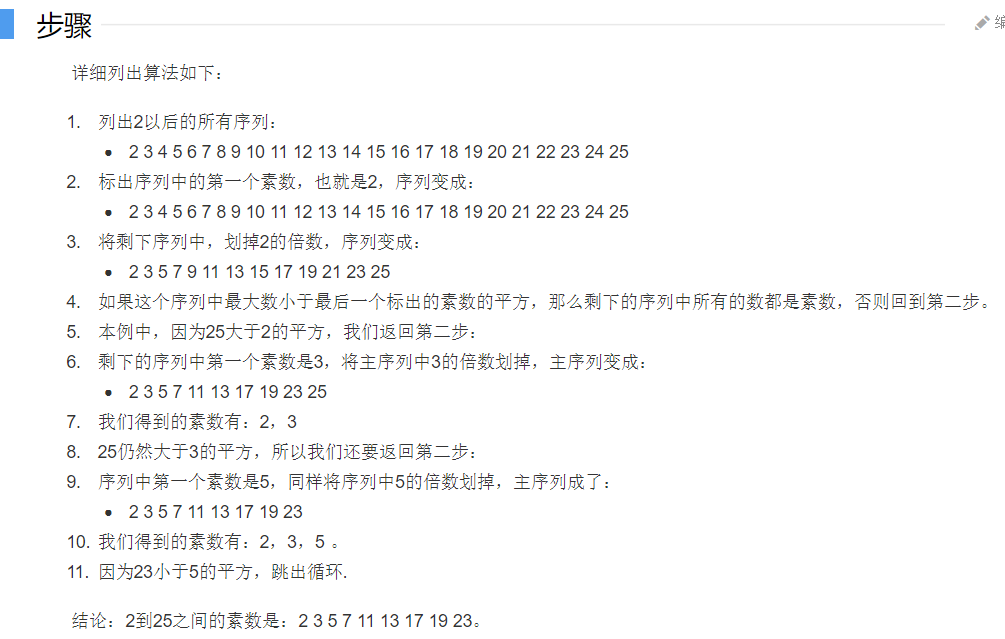
import math
n = int(input("请输入n："))
m = int(math.sqrt(n))
p = [i for i in range(n+1)]
for i in range(2,m+1):
    if p[i]:
        for j in range(2*i,n+1,i):  # 题目中需要填空的地方
            p[j]=0
for i in range(2,n+1):
    if p[i]:
        print(p[i],end=" ") # 需要填空的地方

6、函数返回一个元组（同时返回多个值）

函数返回多个值的方式，是以元组的方式

def fun():
    a = 10
    b = 20
    c = 30
    return a,b,c
r = fun()
print(type(r))

输出结果：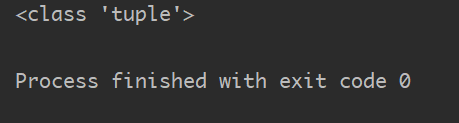

求最大公约数：辗转相除法
求最小公倍数：最小公倍数 = 两数乘积 / 最大公约数

def gcd(m,n):  # 求两个数的最大公约数
    if m < n:
        m,n = n,m
    if m % n == 0:
        return n
    else:
        return gcd(n,m % n)
def lcm(m, n):  # 求两个数的最小公倍数
    # 最小公倍数 = 两数乘积 / 最大公约数
    temp = gcd(m, n)
    return m*n / temp
def func(m,n):
    gongbei = lcm(m,n)
    gongyue = gcd(m,n)
    return gongbei, gongyue
arr = func(27,81)  # 调用func函数  求两个数的最小公倍数和最大公约数
print(type(arr))
print(arr[0])