1. 无向树及其性质

1. 无向树：连通无回路的无向图
   树叶：度数等于1的顶点
   分支点：度数大于等于2的顶点
2. 设G是n阶m条边的无向图，那么以下各个命题是等价的
   1. G是树
   2. G中任意两个顶点之间存在唯一的路径
   3. G是无回路的且m=n-1
   4. G是连通的且m=n-1
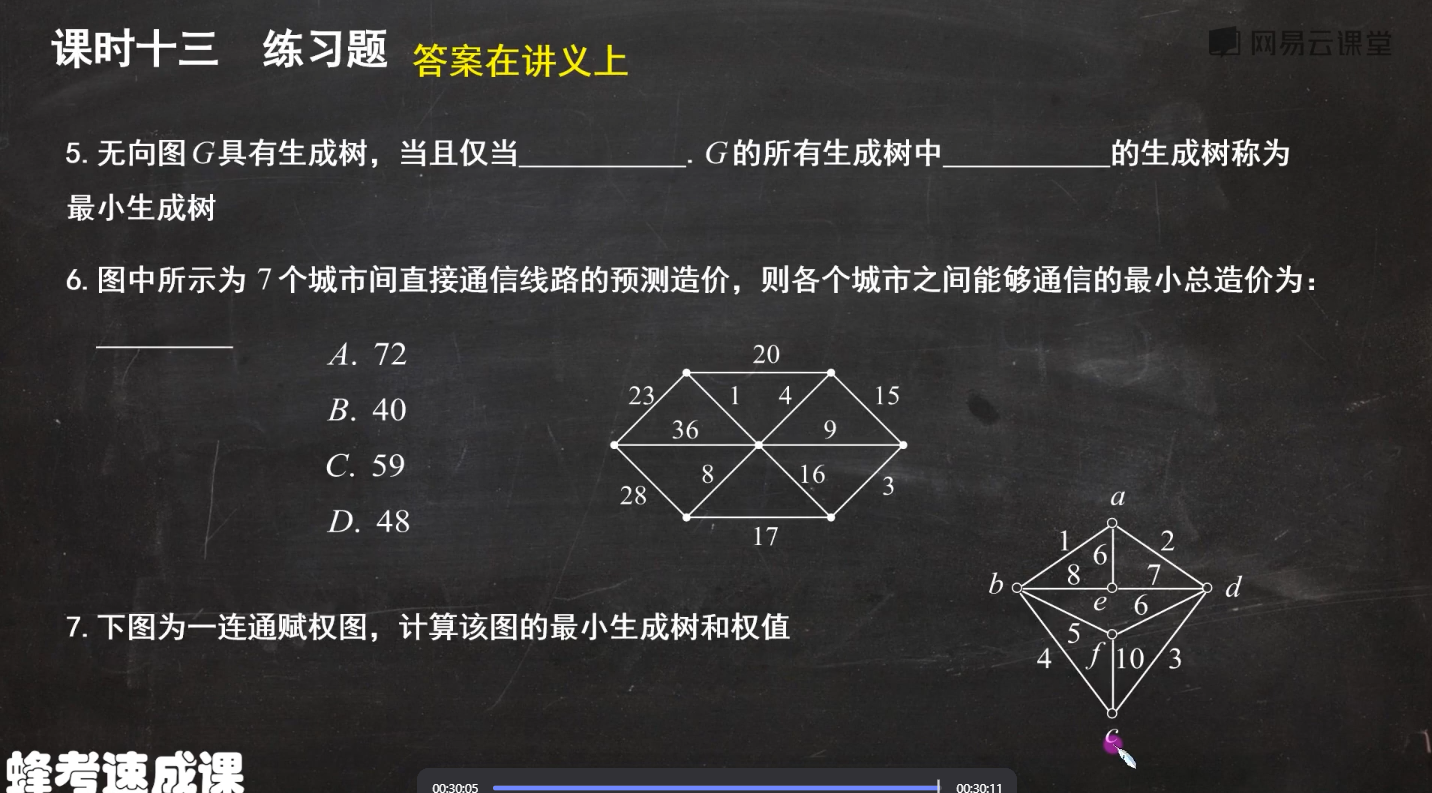
3. 设T是n阶非平凡的无向树，那么T中至少有两片树叶

   例题：树的判定

   
   
   

2. 最小生成树

1. 子图：
2. 生成树：如果无向图G的生成子图T是树，那么就称T是G的生成树
3. 生成树的权：对于无向连通带权图，T是G的一棵生成树，T的各边权之和称为T的权，记作W(T)

4. 最小生成树：G的所有生成树中权最小的生成树

   2.1 例题：如何求最小生成树

   步骤：

5. 给权排序

6. 描点，将边数置0
7. 选边（选择当前带权最小的边，并且不构成回路的）
8. 重复做第三步，直到 边数=顶点数-1

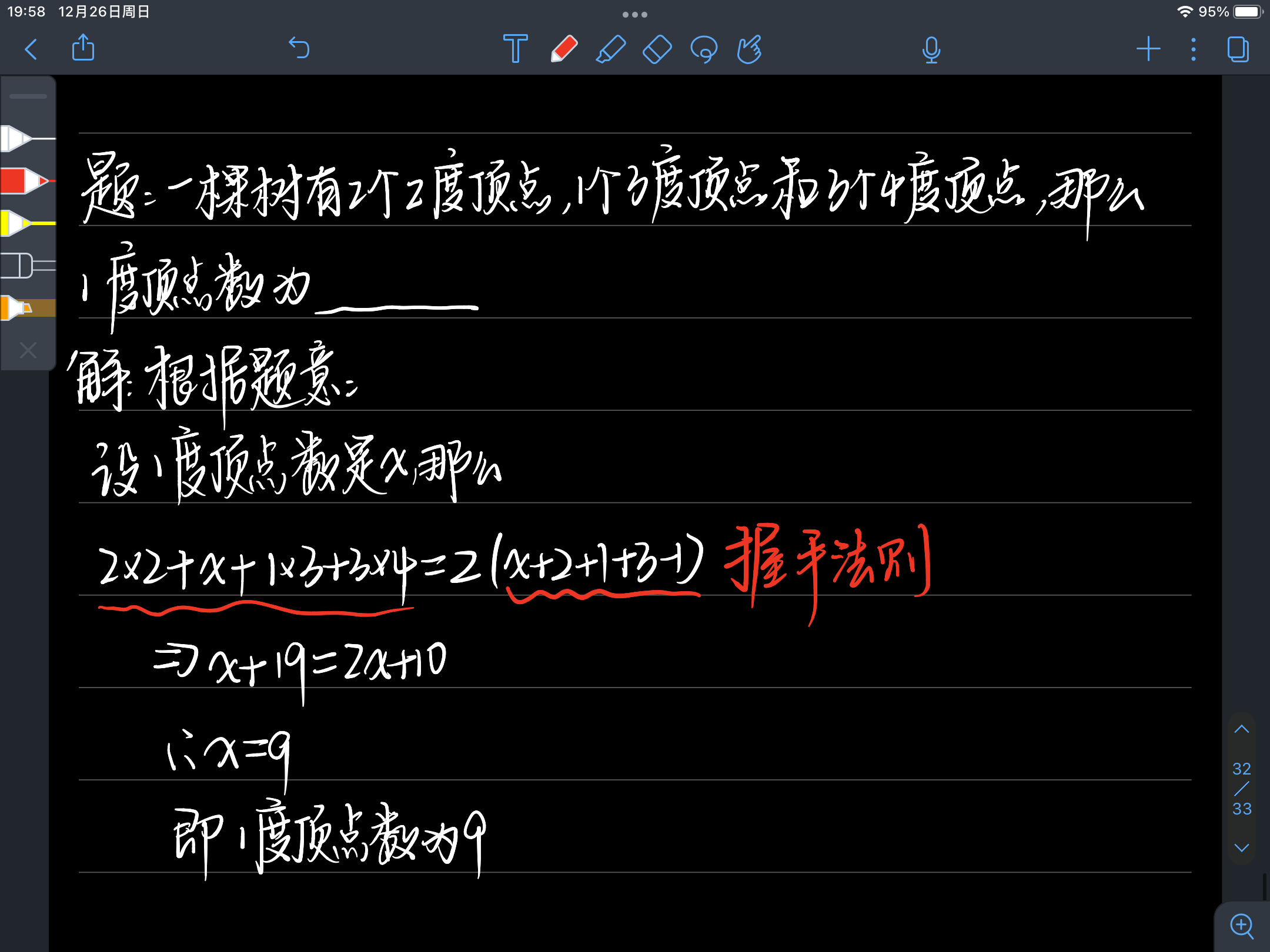
3. 根数及其应用

1. 有向树：如果有向图的基图是无向树，那么就称这个有向图为有向树
   根树：一个顶点入度为0，其余顶点的入度为1的有向树
   层数：从树根到顶点的路径长度（路径中的边数）
   画根树的时候，一般将树根画在最上方，有向边的方向向下或者斜下方，并且省略各个边上的箭头。
2. 祖先：一个结点的根父亲节点
   后代：结点A如果是结点B的子节点，那么就称A是B的后代
   父亲：
   儿子：
   兄弟：
   如果T的每个分支点至多有r个儿子，那么就称T是r叉树。
3. 最优二叉树：权最小的二叉树。二叉树的权等于当前所有树叶节点的权值乘以对应的层数的累加，即：
   

例题：使用哈夫曼算法求最优二叉树

解题步骤：

1. 给权排序
2. 选出两个权最小的顶点，添加新点，权为两个点的和
3. 重复步骤1，2，直到只有一个顶点

例题：求前缀码

2元前缀码：由0-1符号串构成的前缀码
最佳前缀码：由最优二叉树产生的前缀码。左孩子对应的边标记为0，右孩子对应的边标记为1

4. 练习题