一、曲线积分

1、第一类曲线积分

形如下面这种形式的曲线积分，称之为第一类曲线积分，也称之为对弧长的曲线积分。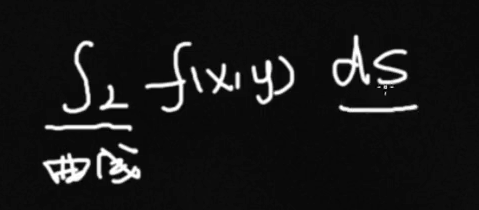

第一类曲线积分的计算方法一般为 三步替换法

  - **替换积分上下限**
  - **替换被积函数**
  - **替换积分因子**

根据积分时坐标系的不同，可以分为以下几种情况：

注意计算第一类曲线积分的时候，积分下限一定要小于积分上限。
例题：

计算对弧长的曲线积分的时候，如果积分变量是常数1，那么积分所得到的即是曲线L的长度，比如下面这道题：

2、第二类曲线积分

（一般不会单独考察，会和格林公式一起出题考察）

例题：

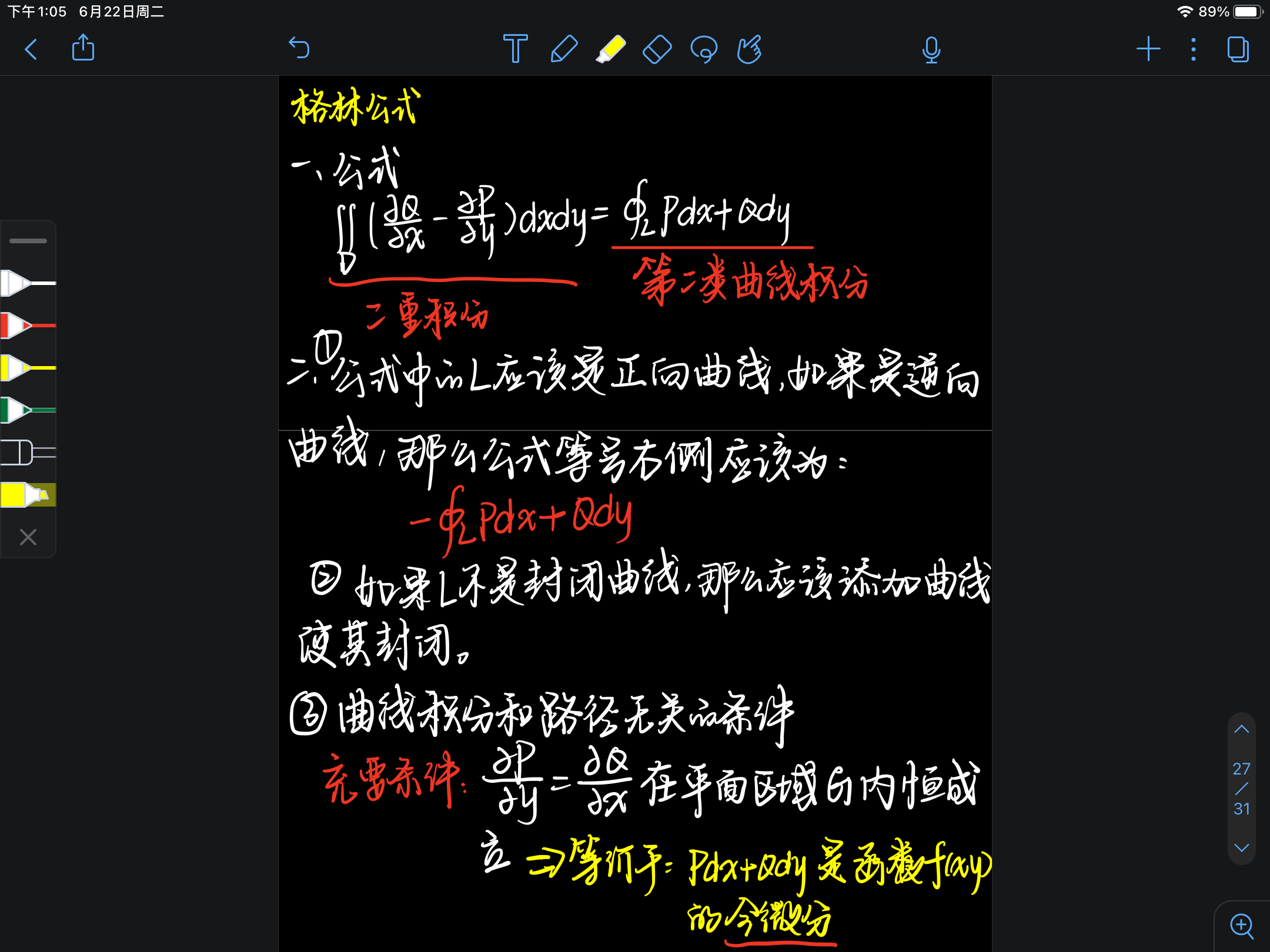
3、格林公式与第二类曲线积分

注意：

• 1、格林公式在期末考试中一般与第二类曲线积分一起考察。
• 2、格林公式可以讲第二类曲线积分转换为二重积分进行运算。
• 3、格林公式中的 L 是指正向的曲线。如果是 逆向 的曲线，那么对应的应该在公式等号右侧添加上负号。
• 4、使用格林公式应该注意积分曲线是否是封闭的曲线，如果不是封闭的曲线，那么应该适当的添加上曲线使其封闭。
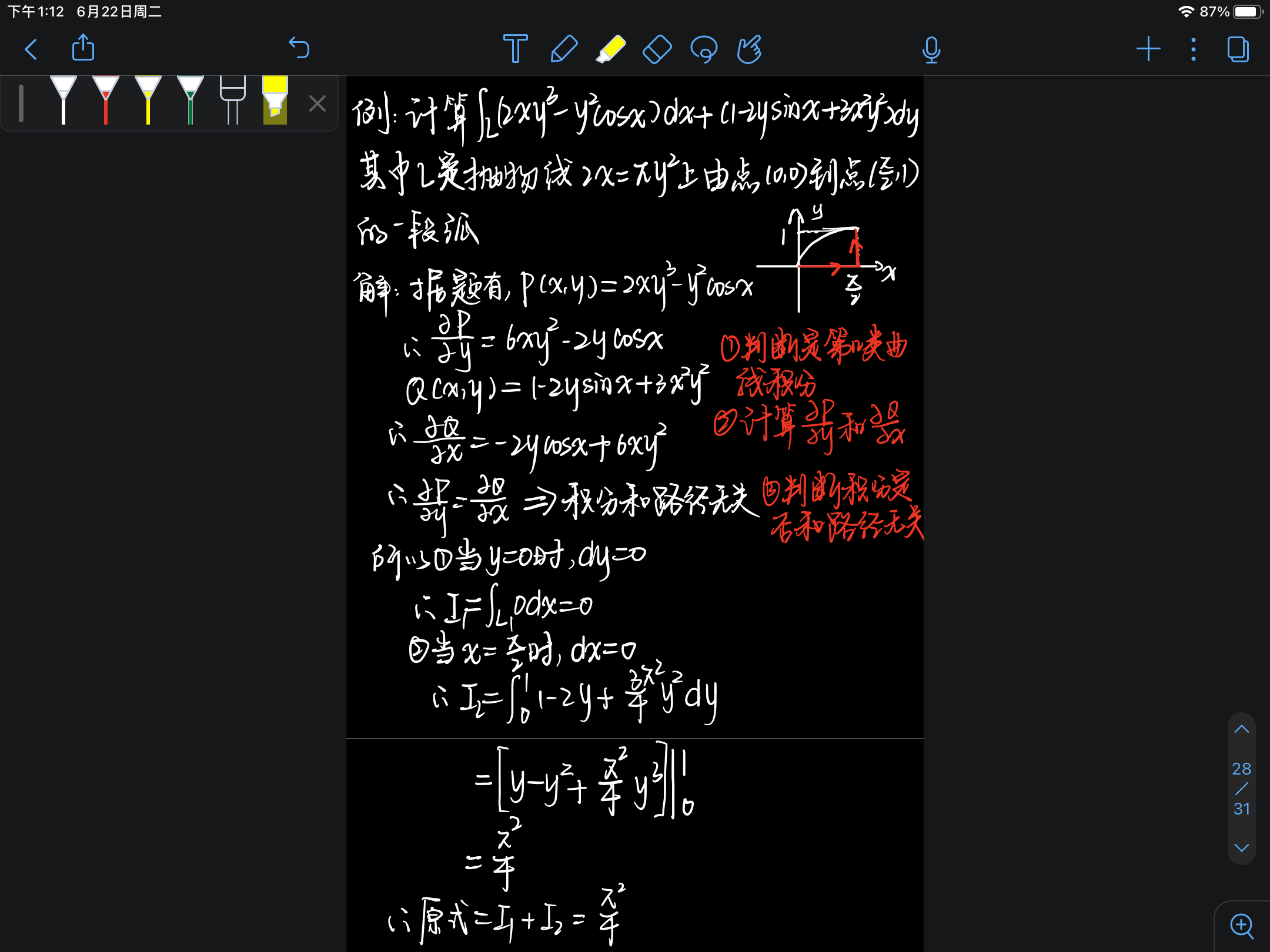
• 5、如果 P(x,y)对y的偏导 等于 Q(x,y)对x的偏导，那么该曲线积分和路径无关。

=>等价的说法：Pdx + Qdy 是函数f(x,y)的全微分

• 6、曲线积分和路径无关的充要条件即是：

P(x,y)对y的偏导 等于 Q(x,y)对x的偏导
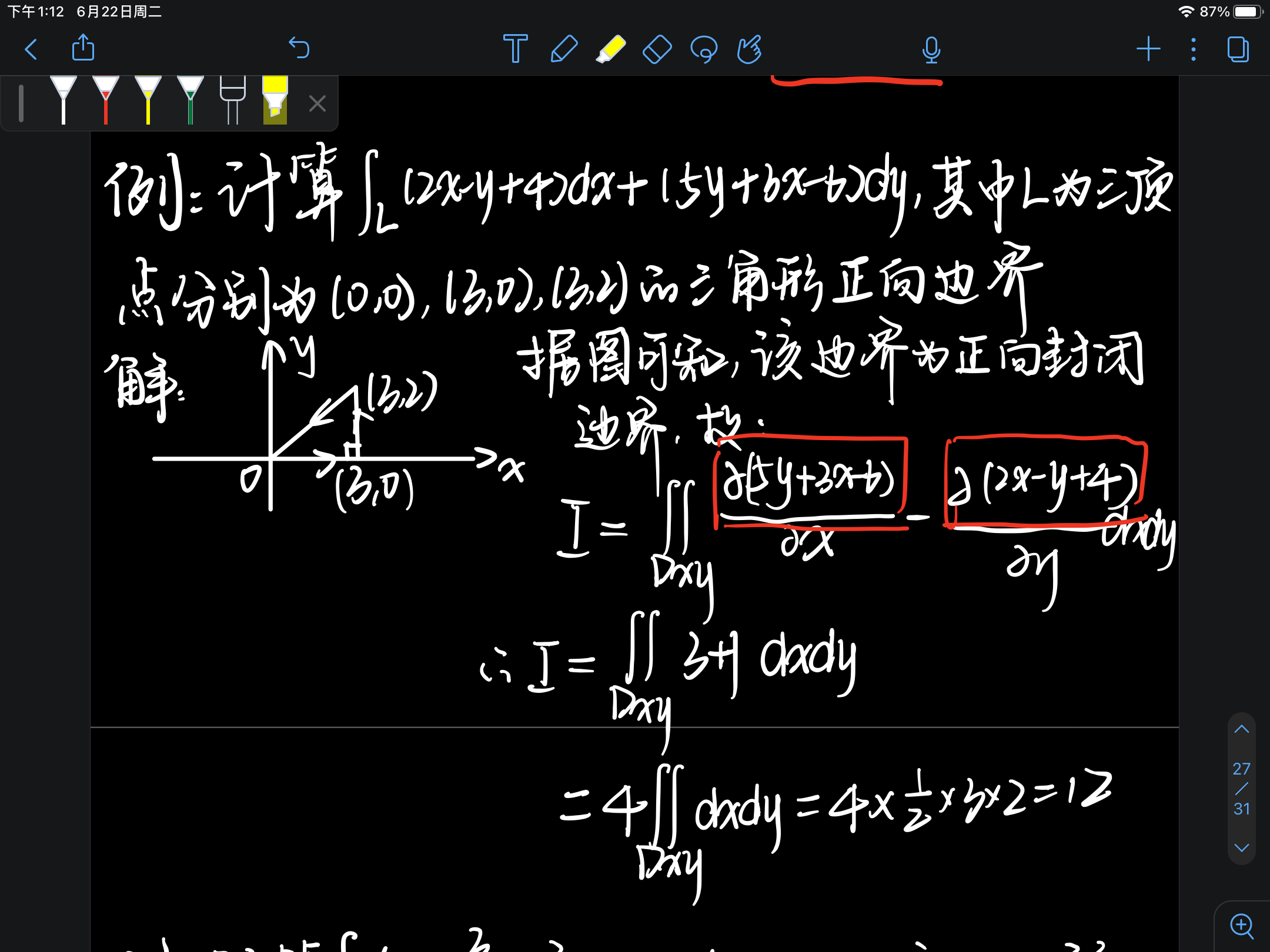
例题：
一般的做题步骤：

• 1、判断是第一类曲线积分还是第二类曲线积分。如果是第二类曲线积分，那么大概率是考察格林公式的使用。
• 2、如果现有的积分曲线L不满足格林公式的使用条件（比如不是封闭的曲线），那么就需要手动的添加上相应的曲线使其满足格林公式的使用条件。记得最后要减去添加上的曲线的曲线积分。
• 3、计算 P对于y的偏导 和 Q对于x的偏导。
• 4、根据第2步判断曲线积分是否与积分路径有关。如果无关，就选择平行于x轴和平行于y轴的直线替换原来的积分曲线L。如果有关，就带入格林公式，转化为二重积分进行计算。

二、曲面积分

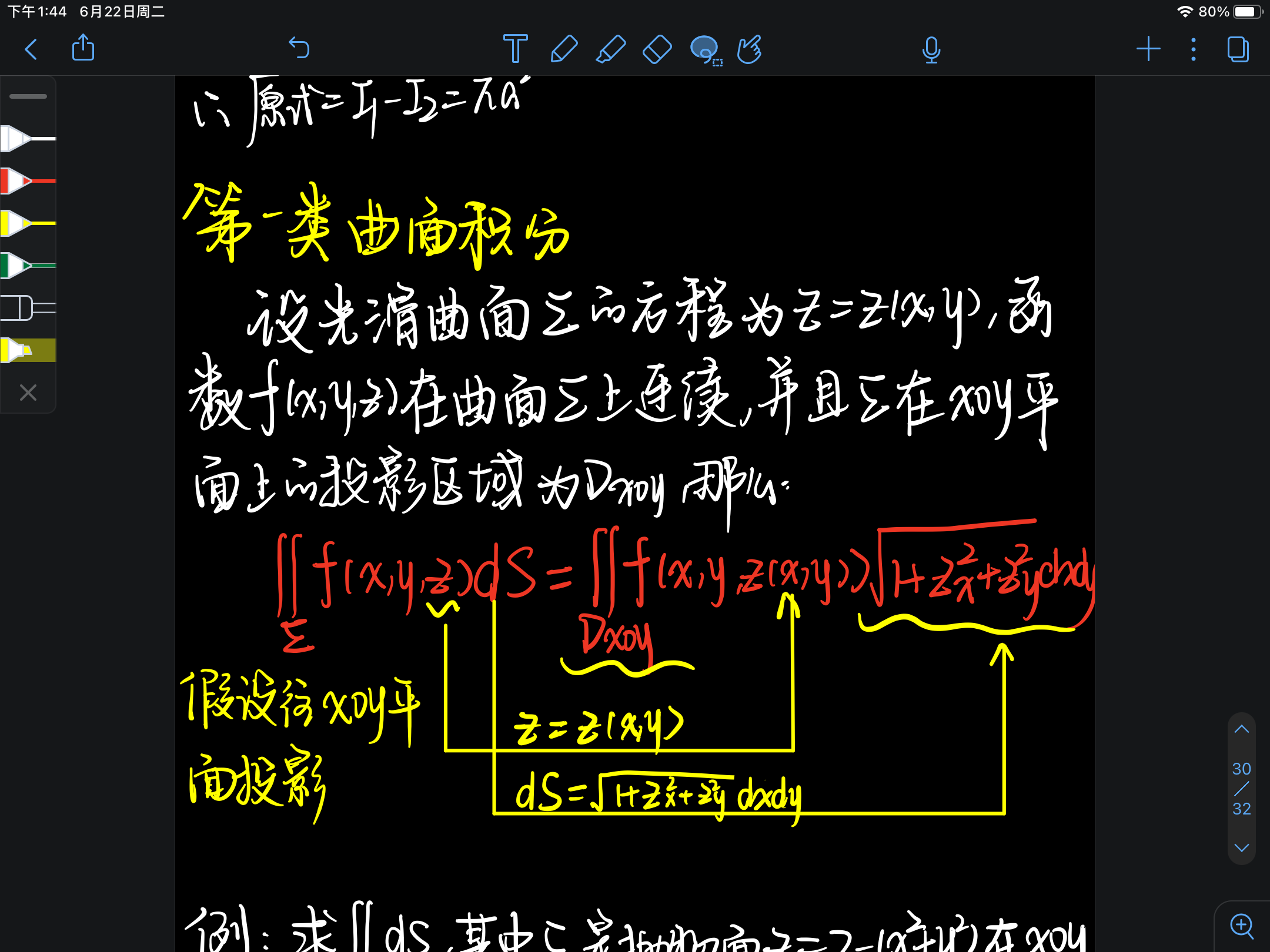
1、第一类曲面积分

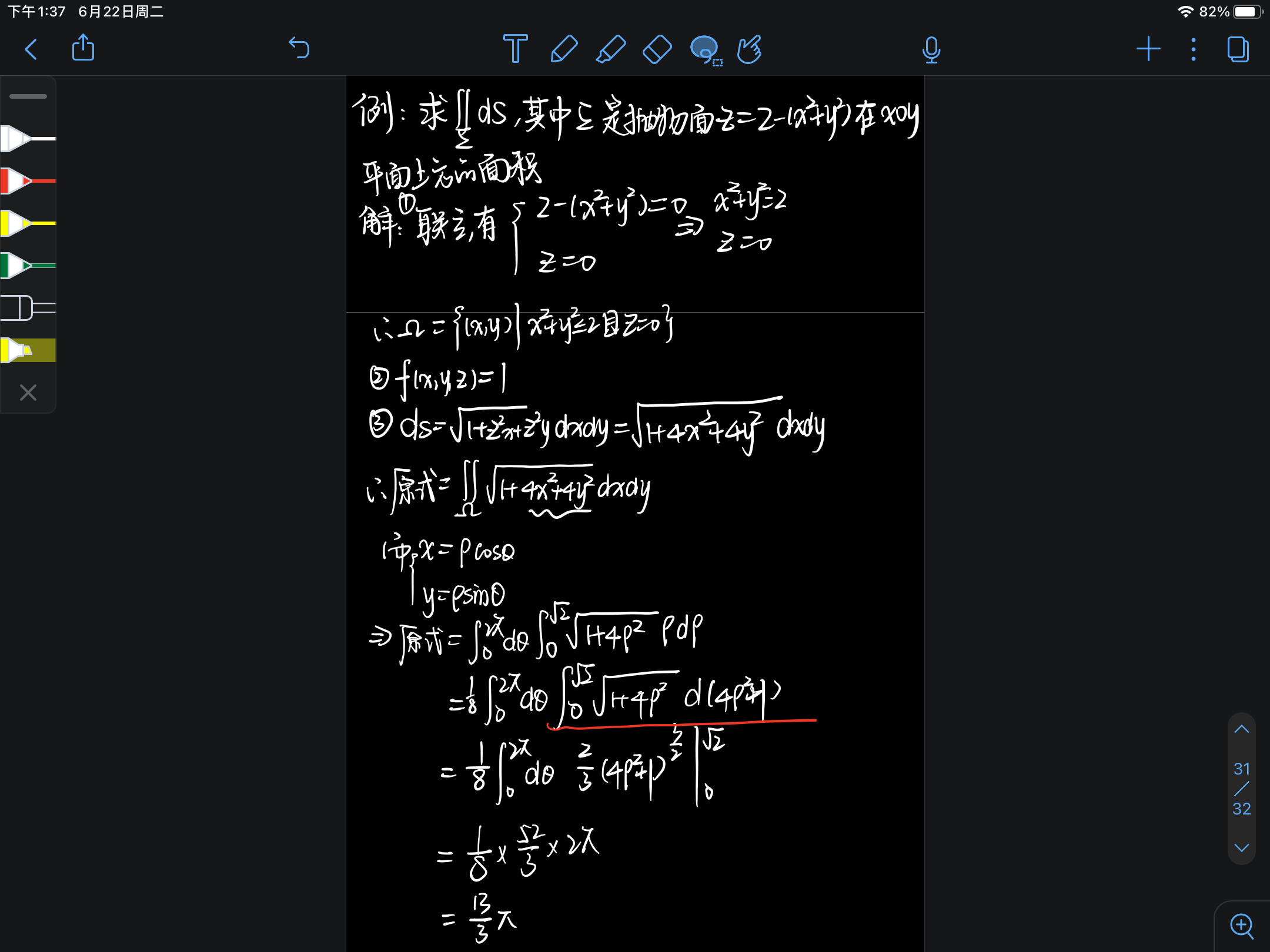
例题：
一般的解题步骤：

• 1、确定是第一类曲面积分还是第二类曲面积分
• 2、确定往xoy平面投影后的平面区域 Ω
• 3、用 z = z(x,y) 替换函数中的z
• 4、用 dxdy替换积分因子ds

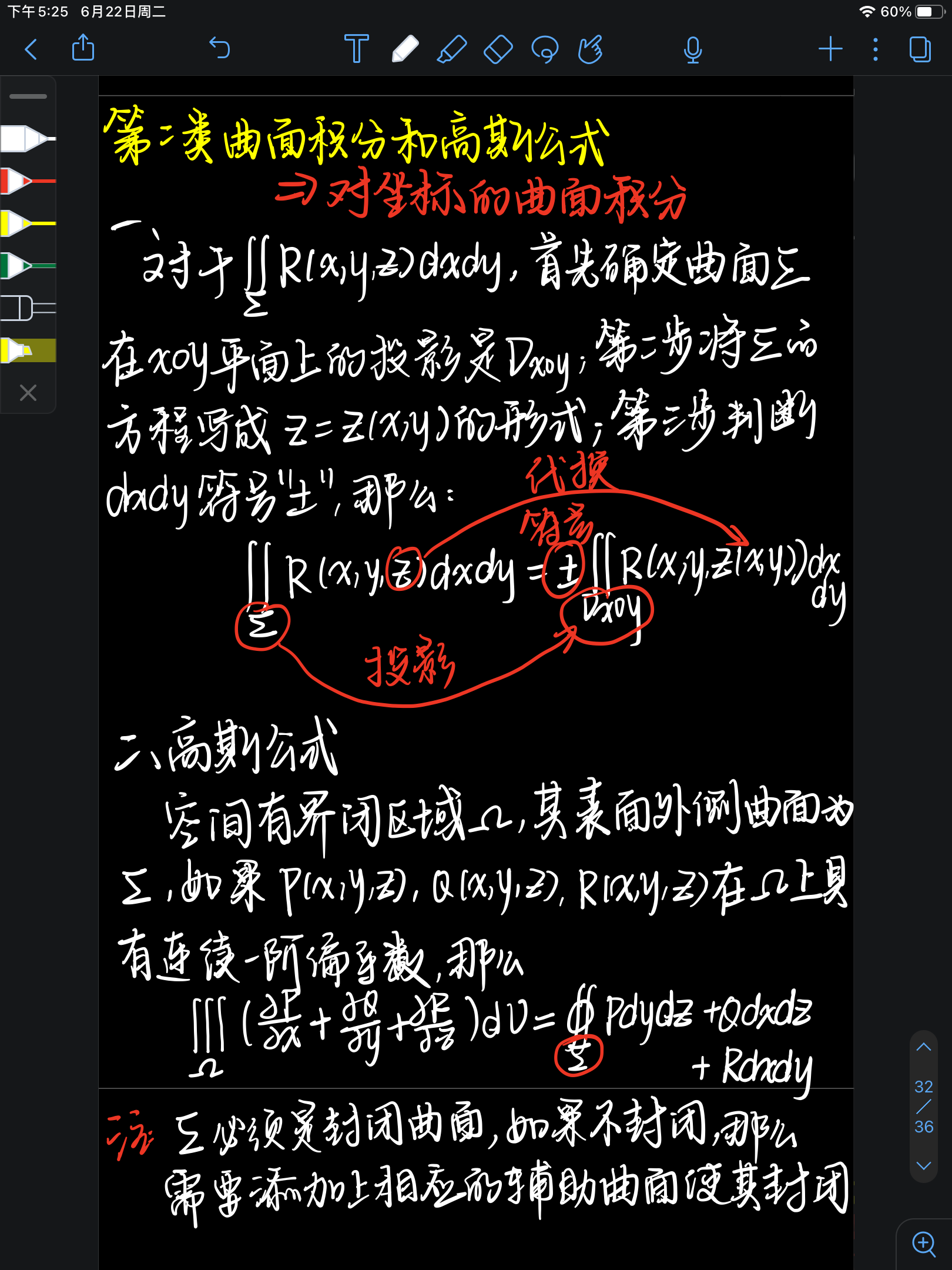
2、第二类曲面积分和高斯公式

将曲面积分的计算转换成三重积分的计算
高斯公式的使用条件：

1. 对各个变量的偏导存在且连续
2. 积分曲面是封闭曲面
3. 
   

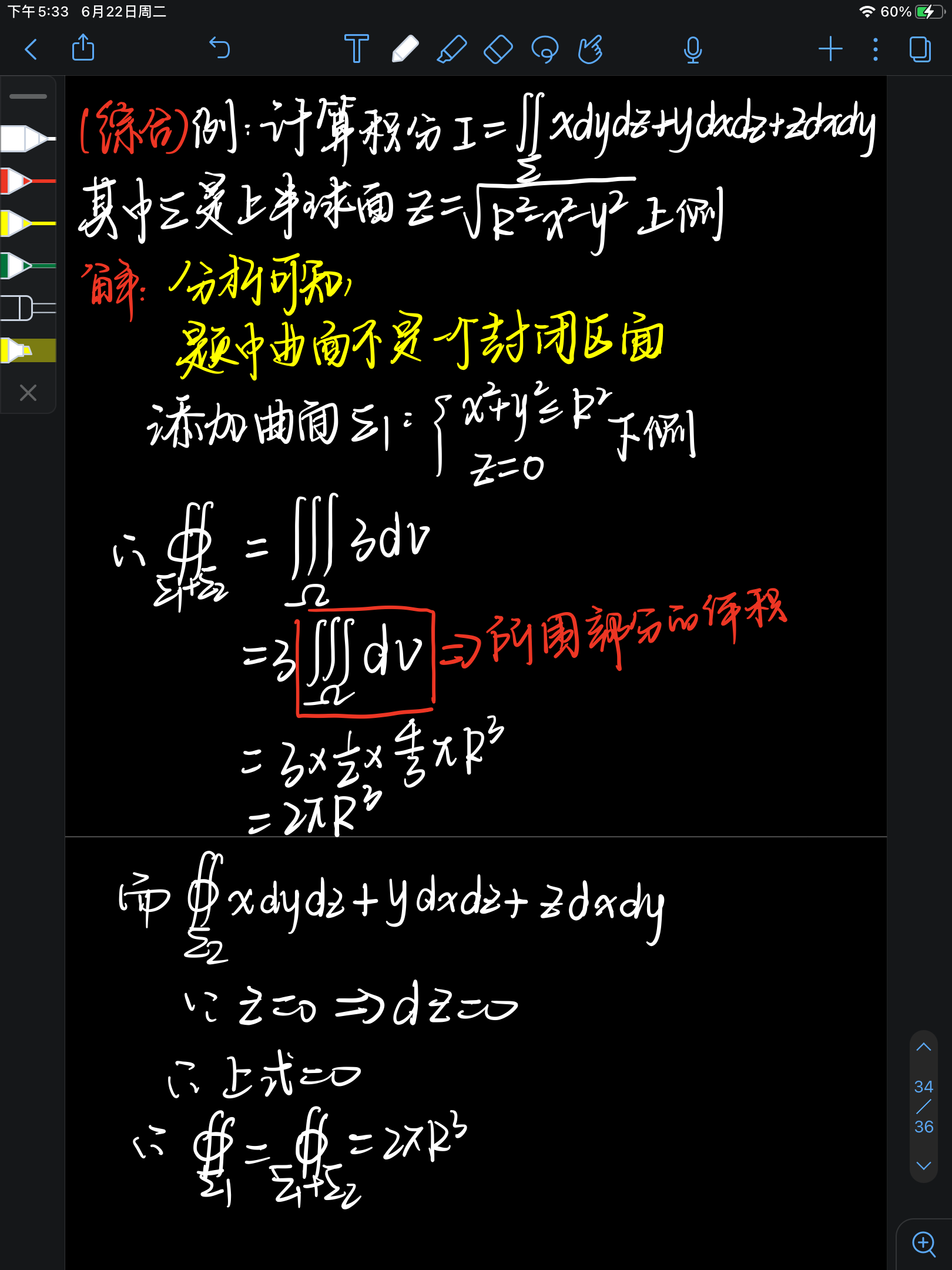
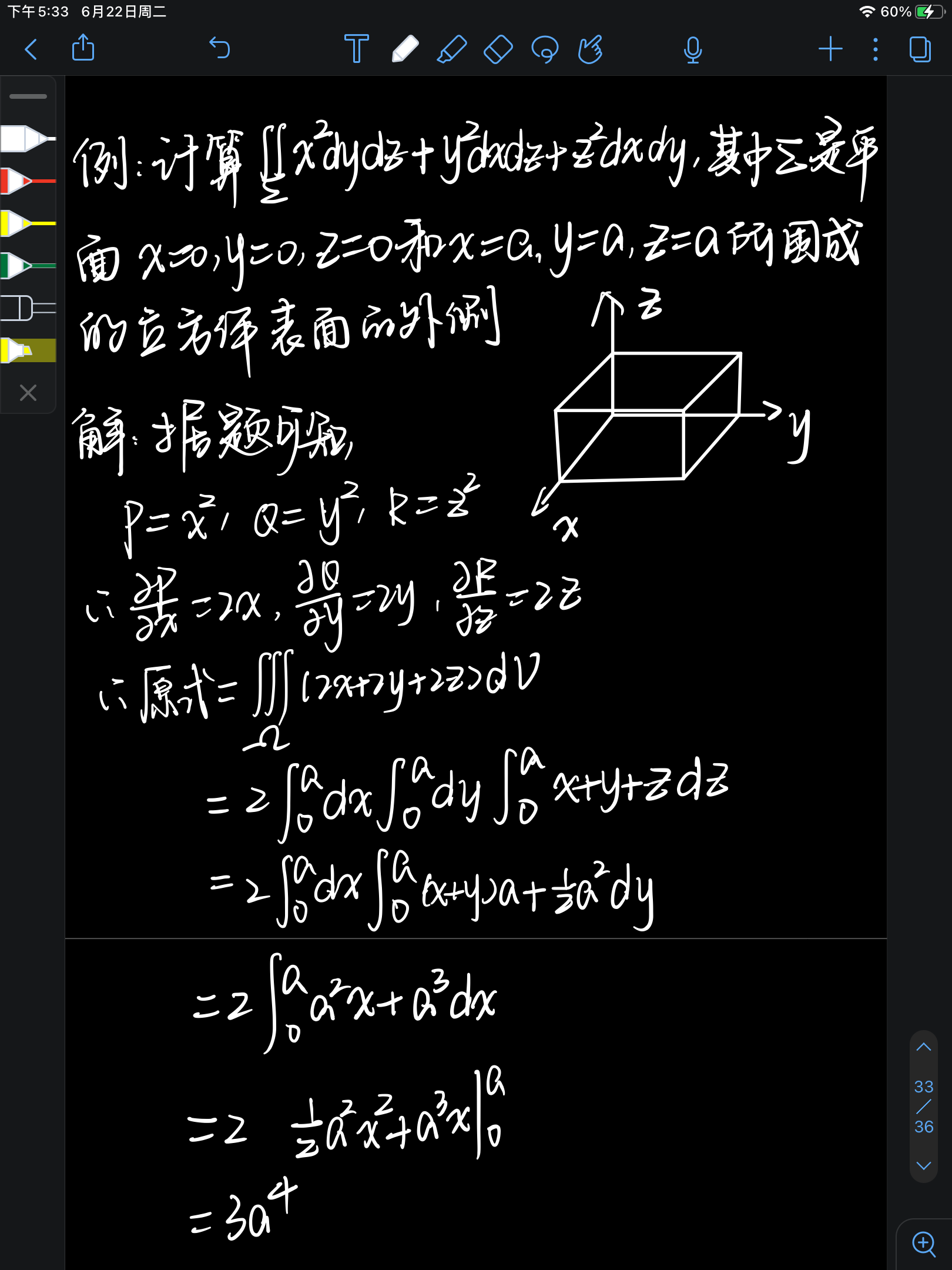
例题：
一般的解题步骤：

1. 求出变量z对于其他各个变量的偏导。
2. 求出投影到xoy平面上的投影区域。
3. 将求出来的偏导代入到高斯公式中。
4. 将第二类曲线积分转换为三重积分计算。
5. 计算三重积分

如果曲面不是封闭的曲面，那么就需要添加适当的曲面使其封闭，然后再减去对应的部分。