转于
最干的干货:
首先,我们的原始目标是,需要根据已有数据推断需要的分布p;当p不容易表达,不能直接求解时,可以尝试用变分推断的方法, 即,寻找容易表达和求解的分布q,当q和p的差距很小的时候,q就可以作为p的近似分布,成为输出结果了。
在这个过程中,我们的关键点转变了,从“求分布”的推断问题,变成了“缩小距离”的优化问题。
举生活中的例子太难了,还是看图说话容易些。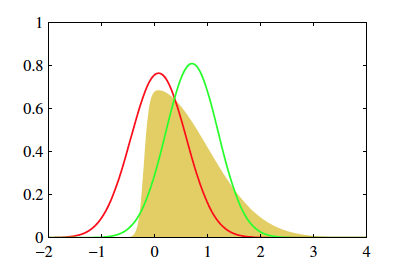
黄色的分布是我们的原始目标p,不好求。它看上去有点像高斯,那我们尝试从高斯分布中找一个红q和一个绿q,分别计算一下p和他们重叠部分面积,选更像p的q作为p的近似分布。
————————-线性逻辑求解思路版———————————
理解变分推断的精华步骤:
- 我们拥有两部分输入:数据x,模型p(z, x)。
- 我们需要推断的是后验概率p(z | x),但不能直接求。
- 构造后验概率p(z | x)的近似分布q(z; v)。
- 不断缩小q和p之间的距离直至收敛。
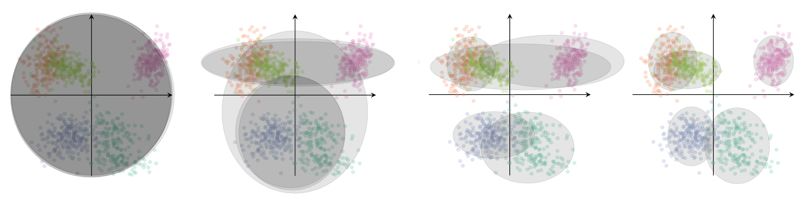
- 变分推断要解决的问题类,叫做概率机器学习问题。简单来说,专家利用他们的知识,给出合理的模型假设p(z, x),其中包括隐含变量z和观察值变量x。(需要说明的是,隐含变量z在通常情况下不止一个,并且相互之间存在依赖关系,这也是问题难求解的原因之一。)为了理解隐含变量和观察值的关系,需要说明一个很重要的概念叫做“生成过程模型”。我们认为,观察值是从已知的隐含变量组成的层次结构中生成出来的。以高斯混合模型问题举例。我们有5个相互独立的高斯分布,分别从中生成很多数据点,这些数据点混合在一起,组成了一个数据集。当我们转换角度,单从每一个数据点出发,考虑它是如何被生成的呢?生成过程分两步,第一步,从5个颜色类中选一个(比如粉红色),然后,再根据这个类对应的高斯分布,生成了这个点在空间中的位置。隐含变量有两个,第一个是5个高斯分布的参数u,第二个是每个点属于哪个高斯分布c,u和c共同组成隐含变量z。u和c之间也存在依赖关系。
2. 后验概率p(z | x)是说,基于我们现有的数据集合x,推断隐含变量的分布情况。利用高斯混合模型的例子来说,就是求得每个高斯分布的参数u的概率和每个数据点的颜色的概率c。根据贝叶斯公式,p(z | x) = p(z, x) / p(x)。 我们根据专家提供的生成模型,可知p(z, x) 部分(可以写出表达式并且方便优化),但是边缘概率p(x),是不能求得的,当z连续时,边缘概率需要对所有可能的z求积分,不好求。当z离散时,计算复杂性随着x的增加而指数增长。
3. 我们需要构造q(z; v),并且不断更新v,使得q(z;v)更接近p(z|x)。首先注意,q(z;v)的表达,意思是z是变量,v是z的概率分布q的参数。所以在构造q的时候也分两步,第一,概率分布的选择。第二,参数的选择。第一步,我们在选择q的概率分布时,通常会直观选择p可能的概率分布,这样能够更好地保证q和p的相似程度。例如高斯混合模型中,原始假设p服从高斯分布,则构造的q依然服从高斯分布。之后,我们通过改变v,使得q不断逼近p。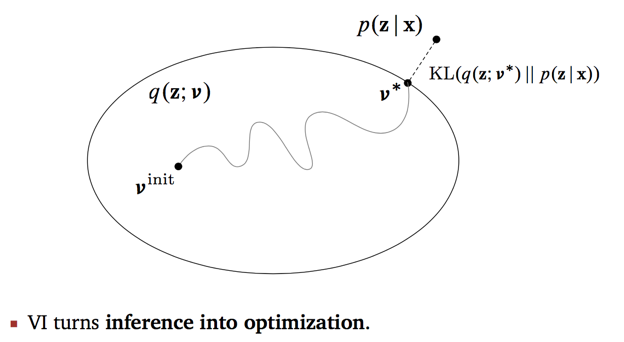
4. 优化问题的求解思路。优化目标很明确,减小KL散度的值即可。然而不幸的是,KL的表达式中依然有一部分不可求的后验概率。这就是为什么会有ELBO的存在原因。利用下面的等式,ELBO中只包括联合概率p(z, x)和q(z; v),从而摆脱后验概率。给定数据集后,最小化KL等价于最大化ELBO,因此ELBO的最大化过程结束时,对应获得的q(z;v*),就成为了我们的最后输出。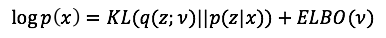
我知道,你就算背过这四步,照样不会做题,因为你尚不能达到”理解“的程度,只算”略知一二“。
———————————追求严谨逻辑的分割线————————————
写在前面:这部分的理解需要一些基本的概率论知识和最优化知识,适合本科生拓展阅读。你需要的是,沉下心来细细琢磨我接下来罗里吧嗦的逻辑,并且前后回顾我提到的数学符号和公式。放心,真正恶心的证明内容,在后面的后面的后面呢。
现在请你忘掉上面看到的东西,听我重头开始讲一个故事。
- Probabilistic Pipeline:
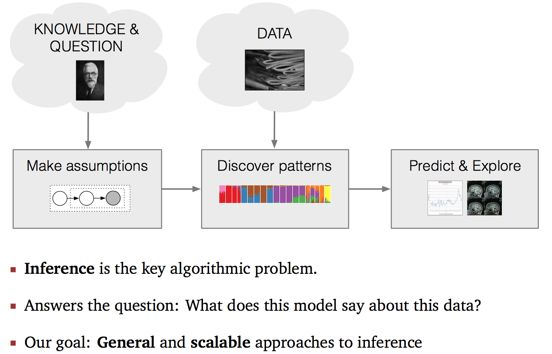
上图是概率机器学习问题的一般求解思路流程图。领域专家拥有知识可以用来建模,并且拥有问题需要被回答。他们依据拥有的知识,给出合理的假设,并且构建出数据的生成过程模型(Generative Processing Model)。模型中主要包括两部分,隐含变量,变量之间的依赖关系。利用该模型,我们希望处理获得的数据,挖掘有价值的模式,然后实现各式各样的Applications。
那么,推断的目的,就是根据我们给定的数据,可以更加细致的刻画生成过程模型中的变量吗?我个人的理解是,专家给出的假设模型相对来说泛化一些,针对不同的数据集,其中的变量的分布(参数值)会有不同,发掘的模式也自然不同。
General和Scalable是两大终极目标,我将要介绍的经典变分推断算法在一定程度上有了非常好的表现。
2. Example: Mixture of Gaussian.
高斯混合模型,作为一种生成过程模型,我们可以数学化定义如下: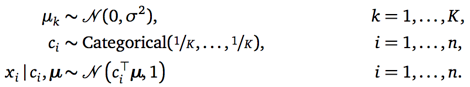
模型混合了K个相互独立的高斯分布(K是超参数),他们的方差被专家定为1(我猜这不是必须的,只是为了简化问题),他们的均值未知,但都是从一个已知的高斯分布中产生的,如第一行所示。
对任一数据点Xi,从模型中生成它的过程分两步。第一步,依据类别分布,选择Xi对应的类标签Ci,如第二行所示;第二步,从类标签Ci对应的高斯分布中产生点Xi,如第三行所示。
更细致的举例说明,如第二篇那个彩色的图,五个分布用不同颜色表示出来,代表五个类。每次从中(均匀的)选择一个类,如第三类粉红色,Ci={0,0,1,0,0} ,然后Xi的抽取依据第三个高斯分布,其均值为Ci*U=U3。自然,该点大概率出现在粉红色类覆盖的区域。
接下来的描述很关键,请别走神。
依据上述假设,专家给出的生成过程模型,包括了三个变量,其中U和C是隐含变量,Xi是观察值变量。更细致的说,U是全局变量,作用发挥在所有数据上,Ci是局部变量,只跟对应数据点Xi相关,与其他点的生成过程无关。他们之间存在的依赖关系,如盘子图所示: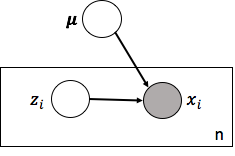
读懂盘子图很简单,一看变量,白圈是隐含变量,盘里的是局部变量,盘外的是全局变量,灰圈是观测值;二看盘子,盘子表示里面的变量zi和xi独立重复n次;三看依赖,箭头表示生成谁需要谁。
基于上述盘子图,我们可以写出表示生成模型的联合概率分布。这个联合概率就看着恶心,其实很好理解,因为,这个等式就是利用盘子图写出来的。仔细瞅,等式右边的三部分分别对应图中三个变量,独立重复的写成连乘形式,有依赖关系的写成条件概率,齐活。必须说明的是,他们三个的分布的形式,其实也是专家在一开始就已经假设好的,通常为基本分布,后续计算使用基本分布的各种特性会容易很多。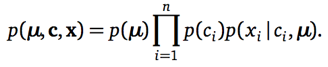
在高斯混合模型问题中,专家需要我们推断什么?事实上,我们的观测数据X,是由没有标签类的点构成的,我们需要根据这些数据集,推断C,每个点是数据哪个颜色类的,并且推断U,每个类对应的高斯分布的均值具体等于什么
3. 从形式化角度,我们到底在推测什么?推测后验概率:给定观测数据x,隐含变量的条件概率。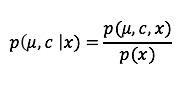
类似上述GMM的例子,我们把问题用更一般的形式表示一下,这个一般形式可以用来描述各种各样的概率机器学习模型。(如果你刚好有一个新问题想用变分推断来解决,尝试套进来)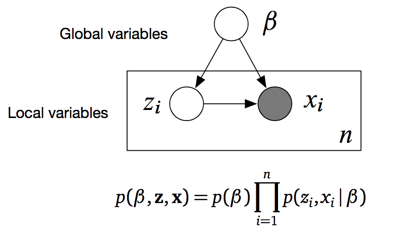
为什么后验不好求?有了联合概率分布,求后验自然而然的想用贝叶斯公式。悲催的是,分母边缘概率intractable,如下公式所示。即使当隐含变量离散(K个值),计算的复杂度(K^n)是会随着数据量n增长呈指数增长趋势的,依然不可计算。
4. 首先解释这个VI主旨图。图中的大圈表示了一个distribution family,参数v是其索引,我们也可以理解为,圈是q的参数v的取值空间,每个点表示每个参数值v对应的q。用高斯混合模型的例子,我们构造q是高斯分布,但是均值参数和方差参数的值不同,代表的分布情况不同,所有的值对应的分布都是这个圈中的一个点。从V-init到V*,这条路径表示我们在迭代过程中,不断缩小的是q与p之间的距离,用KL散度衡量。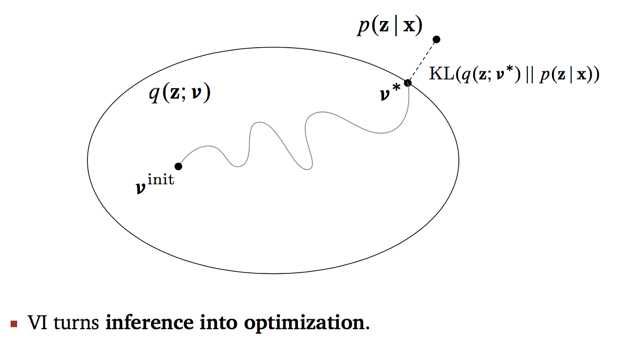
图中的隐含变量z,其实包括了局部变量和全局变量。v也是,对应了所有我们添加的所有的参数。
这里我觉得可以讨论一下KL。什么是KL?KL常被用来衡量两个分布的重叠程度,始终非负。当两个分布完全相同时,KL=0。为什么选KL?Blei的意思是,我们可以选其他的,不过KL makes life easy。我个人认为,针对不同的模型,可以选择其他距离函数,如果能够使得后续优化问题更方便求解。(从DNN过来的同学们请注意,我们这里是在找相似的分布,不能直接单纯用欧氏距离,去判断分布的参数值的增减导致的分布的变化)
5. 关于如何构造q(z;v)。最好的情况,我们知道p的分布是高斯,那么假设q同样是高斯分布,更可能的逼近p。其实不一定要求p是高斯分布,只要它属于exponential family,那么我们把q也放宽,q也属于这个家族即可。因为,exponential family有一个很好的性质( the Hessian of the log normalizer function a _with respect to the natural parameter λ is the covariance matrix of the sufficient statistic vector _t(β))这个性质允许我们很巧妙的简化了自然梯度的推导。事实上这个要求是很宽泛的,家族基本包括了我们常用的大量分布,然而不可否认的是,当p本身不属于这个家族时,q可能永远无法近似p,徘徊遥相望。这是变分推断的固有缺陷,计算结果是一个难以提前估计的近似。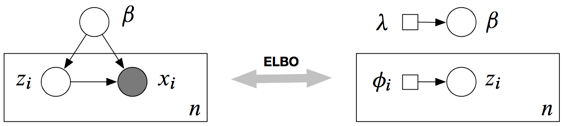
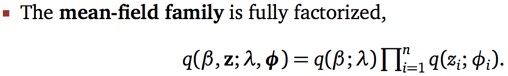
瞅瞅图,原来的分布中,非常重要的变量之间依赖关系,在构造q的时候统统打散,相互独立。它叫做mean-field,是变分推断中最基础最简单的一种构造方式(很多后续研究在用各种方法弥补丢掉的依赖信息)。
如果你有个疑问说,为什么q中没有x了。我的回答是,我们本来想求的条件概率p,是beta和z的联合分布(在给定x的情况下)。那我们的q,也是beta和z的联合分布,并且只由构造的参数决定,与x无关。
我们还是用GMM的例子形象的描述构造过程。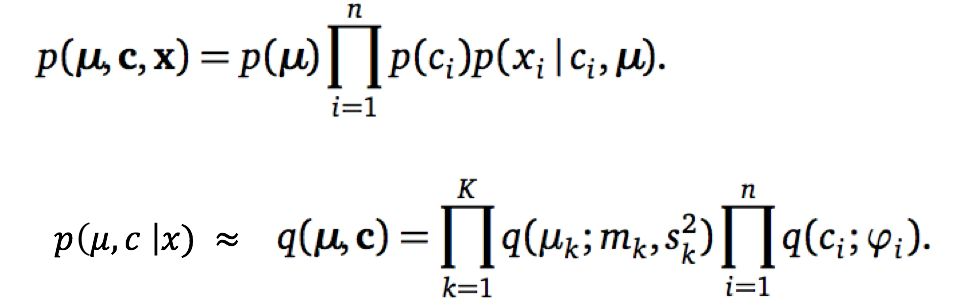
对于5个高斯分布中的某一个Uk,我们构造的q(uk;mk,sk),也属于高斯分布,因此添加了两个变分参数,m是均值,s是标准差。局部变量c_i(表示某个点属于哪一个高斯类),本属于多项式分布,因此在q中它依然是多项式分布,引入变分参数phi_i,phi_i是一个k维向量。
6.ELBO
好消息好消息,ELBO的部分其实知道个大概就可以了,不需要手动推导更新公式(推过也很快会被遗忘),可以直接尝试使用Blei组的开源项目Edword,实现自动求导求更新公式的功能。
完结。谢谢大家的赞。

