子序列问题 - leetcode-115：不同的子序列 - 《算法珠玑》

问题
思路

问题

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数
字符串的一个子序列是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，”ACE” 是 “ABCDE” 的一个子序列，而 “AEC” 不是）

题目数据保证答案符合 32 位带符号整数范围

示例 1：
输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
有 3 种可以从 s 中得到 “rabbit” 的方案

示例 2：
输入：s = "babgbag", t = "bag"
输出：5
解释：
如下图所示, 有 5 种可以从 s 中得到 “bag” 的方案。
(上箭头符号 ^ 表示选取的字母)
babgbag
^^ ^
babgbag
^^ ^
babgbag
^ ^^
babgbag
^ ^^
babgbag
^^^

思路

这道题目如果不是子序列，而是要求连续序列的，那就可以考虑用KMP
来看看动规五部曲分析如下：

确定dp数组以及下标的含义
- dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]
确定递推公式
- 这一类问题，基本是要分析两种情况
  - s[i - 1] 与 t[j - 1]相等
  - s[i - 1] 与 t[j - 1]不相等
- 当s[i - 1]与t[j - 1]相等时，dp[i][j]可以有两部分组成
  - 一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]
  - 一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]
- 为什么还要考虑不用s[i - 1]来匹配，都相同了指定要匹配啊
  - 例如：s：bagg 和 t：bag ，s[3]和t[2]是相同的，但是字符串s也可以不用s[3]来匹配，即用s[0]s[1]s[2]组成的bag；当然也可以用s[3]来匹配，即：s[0]s[1]s[3]组成的bag
  - 所以当s[i - 1]与t[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
- 当s[i - 1]与t[j - 1]不相等时，dp[i][j]只有一部分组成，不用s[i - 1]来匹配，即：dp[i - 1][j]
- 所以递推公式为：dp[i][j] = dp[i - 1][j];
dp数组如何初始化
- 从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][0]和dp[0][j]是一定要初始化的
- dp[i][0]表示什么呢？
  - dp[i][0] 表示：以i-1为结尾的s可以随便删除元素，出现空字符串的个数
  - 那么dp[i][0]一定都是1，因为也就是把以i-1为结尾的s，删除元素，出现空字符串的个数，就是1
  - 再来看dp[0][j]，dp[0][j]：空字符串s可以随便删除元素，出现以j-1为结尾的字符串t的个数
  - 那么dp[0][j]一定都是0，s无论如何也变成不了t
  - 最后就要看一个特殊位置了，即：dp[0][0] 应该是多少
  - dp[0][0]应该是1，空字符串s，可以删除0个元素，变成空字符串t ```java int[][] dp = new int[s.length() + 1][t.length() + 1];

for(int i=0; i < s.length() + 1; i++) dp[i][0] = 1;


- 确定遍历顺序
   - 从递推公式`dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];`和`dp[i][j] = dp[i - 1][j];` 中可以看出`dp[i][j]`都是根据左上方和正上方推出来的
   - 所以遍历的时候一定是从上到下，从左到右，这样保证dp[i][j]可以根据之前计算出来的数值进行计算
```java
for(int i = 1; i <= s.length(); i++){
    for(int j = 1; j <= t.length(); j++){
        if((s.charAt(i - 1)) == (t.charAt(j - 1)))
            dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
        else
            dp[i][j] = dp[i - 1][j];
    }
}

举例推导dp数组
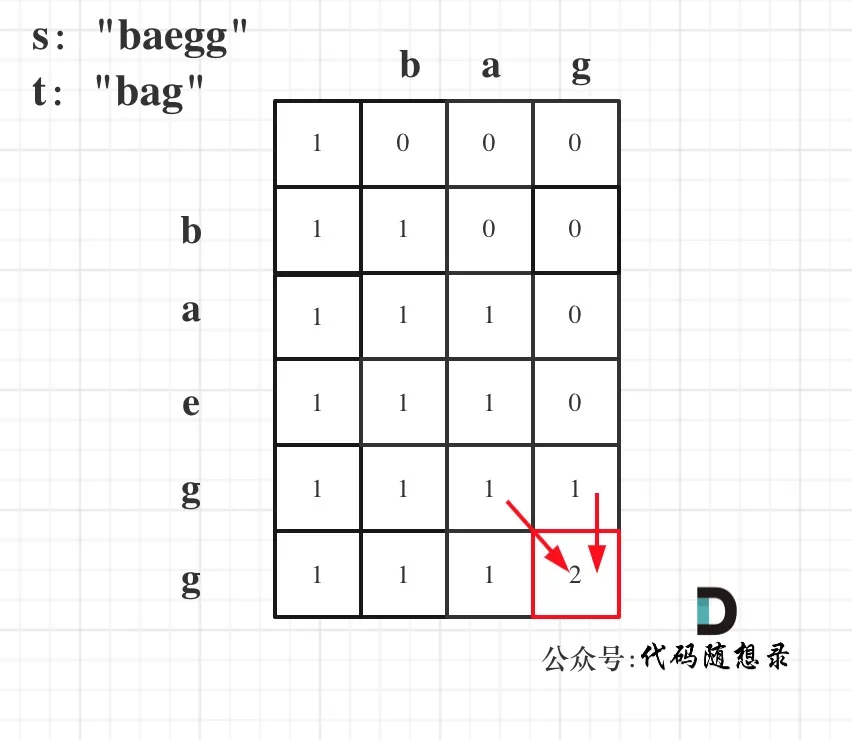
- 以s：”baegg”，t：”bag”为例，推导dp数组状态如下：

class Solution {
    public int numDistinct(String s, String t) {
        int[][] dp = new int[s.length() + 1][t.length() + 1];

        for(int i = 0; i < s.length() + 1; i++) 
            dp[i][0] = 1;

        for(int i = 1; i <= s.length(); i++){
            for(int j = 1; j <= t.length(); j++){
                if((s.charAt(i - 1)) == (t.charAt(j - 1)))
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                else
                    dp[i][j] = dp[i - 1][j];
            }
        }
        return dp[s.length()][t.length()];
    }
}