leetcode-300：最长递增子序列

问题

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度
子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列

示例 1：
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4

示例 2：
输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：
输入：nums = [7,7,7,7,7,7,7]
输出：1

思路

最长上升子序列是动规的经典题目，这里dp[i]是可以根据dp[j]（j < i）推导出来的，那么依然用动规五部曲来分析详细一波：

• dp[i]的定义

  • **dp[i]**表示**i**之前包括**i**的最长上升子序列

• 状态转移方程

  • 位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值
  • 所以：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
  • 注意这里不是要**dp[i]**与**dp[j] + 1**进行比较，而是我们要取**dp[j] + 1**的最大值

• dp[i]的初始化

  • 每一个i，对应的dp[i]（即最长上升子序列）起始大小至少都是是1

• 确定遍历顺序

  • dp[i] 是由0到i-1各个位置的最长升序子序列推导而来，那么遍历i一定是从前向后遍历
  • j其实就是0到i-1，遍历i的循环在外层，遍历j则在内层，代码如下：

    for (int i = 1; i < nums.length; i++) {
    for (int j = 0; j < i; j++) {
       if (nums[i] > nums[j]) 
           dp[i] = max(dp[i], dp[j] + 1);
    }
    if (dp[i] > result) 
       result = dp[i]; // 取长的子序列
    }

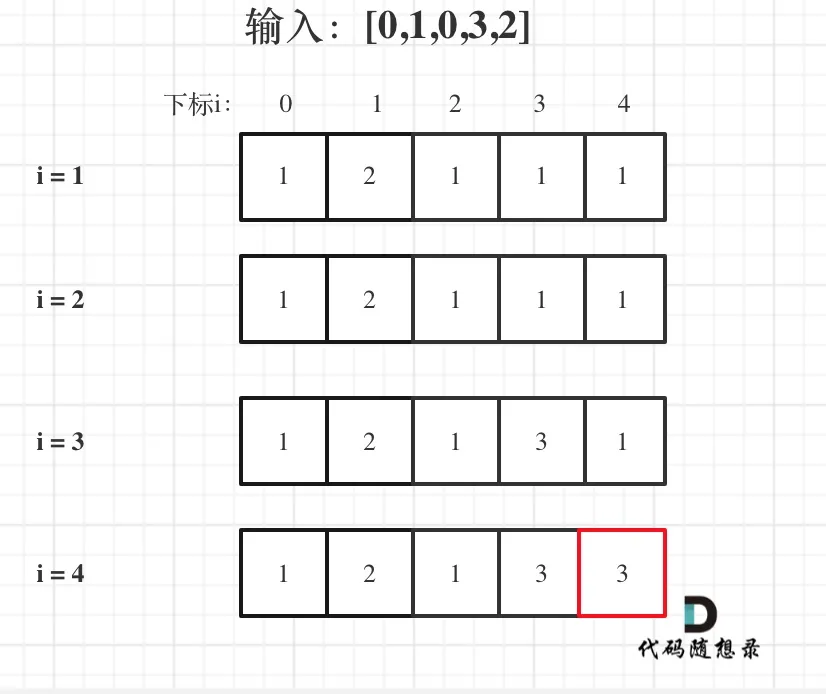
• 举例推导dp数组

  • 输入：[0,1,0,3,2]，dp数组的变化如下：

class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums.length <= 1) 
            return nums.length;
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        int result = 0;
        for (int i = 1; i < nums.length; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) 
                    dp[i] = Math.max(dp[i], dp[j] + 1);
            }
            if (dp[i] > result) 
                result = dp[i]; // 取长的子序列
        }
        return result;
    }
}