问题

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node的新值等于原树中大于或等于node.val的值之和
提醒一下，二叉搜索树满足下列约束条件：

  • 节点的左子树仅包含键小于节点键的节点
  • 节点的右子树仅包含键大于节点键的节点
  • 左右子树也必须是二叉搜索树

示例 1：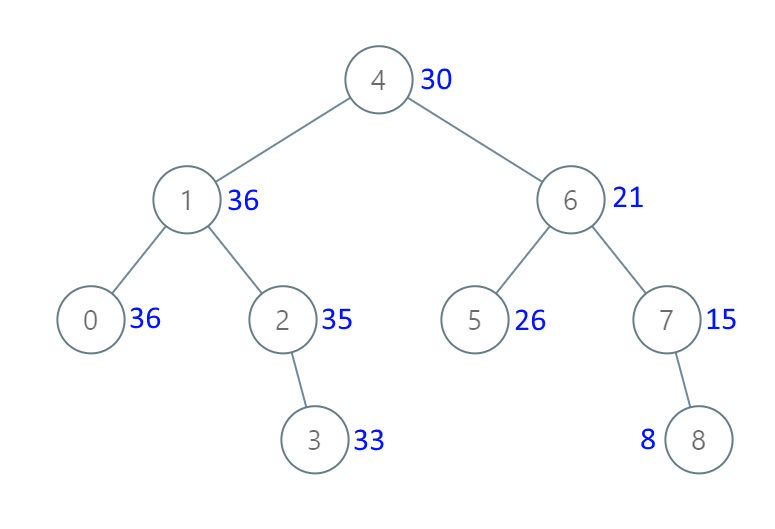
leetcode-538：把二叉搜索树转换为累加树 - 图1

输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：
输入：root = [0,null,1]
输出：[1,null,1]

示例 3：
输入：root = [1,0,2]
输出：[3,3,2]

示例 4：
输入：root = [3,2,4,1]
输出：[7,9,4,10]

解法一：递归

反中序遍历二叉搜索树，记录过程中的节点值之和，顺序累加，并不断更新当前遍历到的节点的节点值

  1. class Solution {
  2.     int sum = 0;
  3.     public TreeNode convertBST(TreeNode root) {
  4.         if(root != null){
  5.             convertBST(root.right);
  6.             sum += root.val;
  7.             root.val = sum;
  8.             convertBST(root.left);
  9.         }
  10.         return root;
  11.     }
  12. }
  • 时间复杂度：leetcode-538：把二叉搜索树转换为累加树 - 图2，其中 n 是二叉搜索树的节点数。每一个节点恰好被遍历一次
  • 空间复杂度：leetcode-538：把二叉搜索树转换为累加树 - 图3，为递归过程中栈的开销，平均情况下为 leetcode-538：把二叉搜索树转换为累加树 - 图4，最坏情况下树呈现链状，为 leetcode-538：把二叉搜索树转换为累加树 - 图5

可以通过一个pre指针记录当前遍历节点cur的前一个结点

  • 递归函数参数以及返回值

    • 不需要返回值
    • 定义一个全局变量pre，用于保存cur节点的前一个节点的数值
      1. int pre;
      2. void traversal(TreeNode cur);

  • 确定终止条件

    1. if(cur == null) return null;

  • 确定单层递归逻辑

    • 右中左来遍历二叉树，中节点的处理逻辑就是让cur加上前一个节点的数值

      1. traversal(cur.right);
      2. cur.val += pre;
      3. pre = cur.val;
      4. traversal(cur.left);
      1. class Solution {
      2. int pre; // 记录前一个节点的数值
      3. void traversal(TreeNode cur) { // 右中左遍历
      4.    if (cur == null) return;
      5.    traversal(cur.right);
      6.    cur.val += pre;
      7.    pre = cur.val;
      8.    traversal(cur.left);
      9. }
      11. public TreeNode convertBST(TreeNode root) {
      12.    pre = 0;
      13.    traversal(root);
      14.    return root;
      15. }
      16. }

解法二：迭代

  1. class Solution {
  2.     int pre; // 记录前一个节点的数值
  4.     public void traversal(TreeNode root) {
  5.         Deque<TreeNode> st = new LinkedList<TreeNode>();
  6.         TreeNode cur = root;
  8.         while (cur != null || !st.isEmpty()) {
  9.             if (cur != null) {
  10.                 st.push(cur);
  11.                 cur = cur.right;   // 右
  12.             } else {
  13.                 cur = st.pop();     // 中
  14.                 cur.val += pre;
  15.                 pre = cur.val;
  16.                 cur = cur.left;    // 左
  17.             }
  18.         }
  19.     }
  21.     public TreeNode convertBST(TreeNode root) {
  22.         pre = 0;
  23.         traversal(root);
  24.         return root;
  25.     }
  26. }