问题

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用

一般来说，删除节点可分为两个步骤：

  • 首先找到需要删除的节点
  • 如果找到了，删除它

说明： 要求算法时间复杂度为 O(h)，h 为树的高度

示例:
root = [5,3,6,2,4,null,7]
key = 3

  1. 5<br />   / \<br />  3   6<br /> / \   \<br />2   4   7

给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它

一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。

5<br />   / \<br />  4   6<br /> /     \<br />2       7

另一个正确答案是 [5,2,6,null,4,null,7]

5<br />   / \<br />  2   6<br />   \   \<br />    4   7

解法一：递归

递归三部曲：

  • 确定递归函数参数以及返回值

  • 确定终止条件

    • 遇到空返回，其实这也说明没找到删除的节点，遍历到空节点直接返回了
      if (root == null) return root;

  • 确定单层递归的逻辑

有以下五种情况：

  • 第一种情况：没找到删除的节点，遍历到空节点直接返回了
  • 找到删除的节点
    • 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回null为根节点
    • 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
    • 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
    • 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点

第五种情况有点难以理解，看下面动画：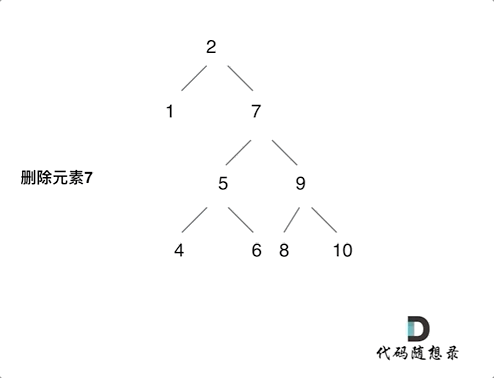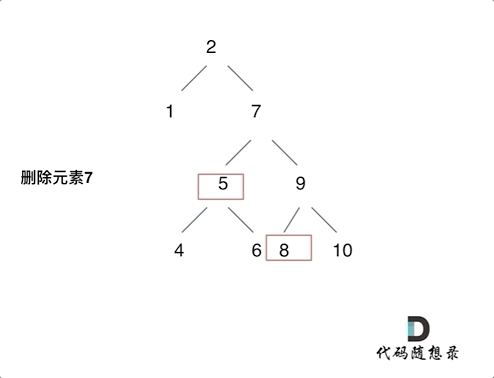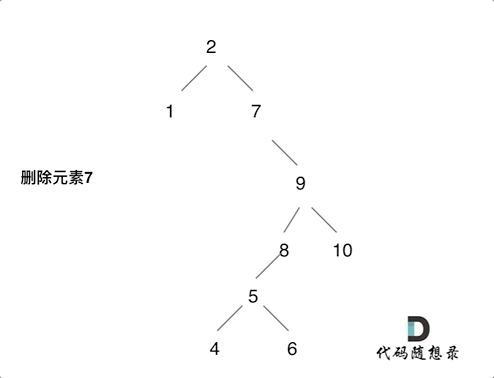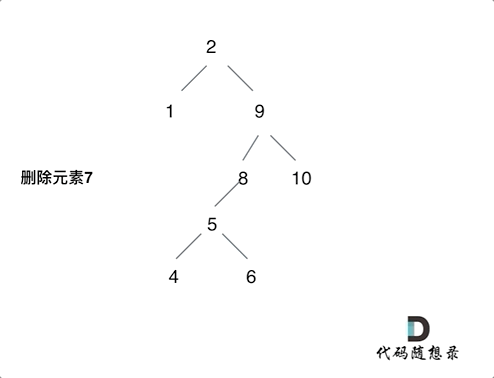
leetcode-450：删除二叉搜索树中的节点 - 图1
动画中颗二叉搜索树中，删除元素7， 那么删除节点（元素7）的左孩子就是5，删除节点（元素7）的右子树的最左面节点是元素8

将删除节点（元素7）的左孩子放到删除节点（元素7）的右子树的最左面节点（元素8）的左孩子上，就是把5为根节点的子树移到了8的左孩子的位置

要删除的节点（元素7）的右孩子（元素9）为新的根节点

这样就完成删除元素7的逻辑

if (root.val == key) {
    // 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回null为根节点
    // 第三种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点
    if (root.left == null) 
        return root.right; 
    // 第四种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
    else if (root.right == null) 
        return root.left; 
    // 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点
    的左孩子的位置并返回删除节点右孩子为新的根节点
    else {  
        TreeNode cur = root.right; // 找右子树最左面的节点
        while(cur.left != null) { 
            cur = cur.left;
        }
        cur.left = root.left; // 把要删除的节点（root）左子树放在cur的左孩子的位置
        root = root.right;     // 返回旧root的右孩子作为新root
        return root;
    }
}

这里相当于把新的节点返回给上一层，上一层就要用 root.left 或者 root.right接住

if (root.val > key) 
    root.left = deleteNode(root.left, key);
if (root.val < key) 
    root.right = deleteNode(root.right, key);
return root;

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) 
            return root; // 第一种情况：没找到删除的节点，遍历到空节点直接返回了
        if (root.val == key) {
            // 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回null为根节点
            // 第三种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点
            if (root.left == null) 
                return root.right; 
            // 第四种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
            else if (root.right == null) 
                return root.left; 
            // 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点
            的左孩子的位置并返回删除节点右孩子为新的根节点
            else {  
                TreeNode cur = root.right; // 找右子树最左面的节点
                while(cur.left != null) { 
                    cur = cur.left;
                }
                cur.left = root.left; // 把要删除的节点（root）左子树放在cur的左孩子的位置
                root = root.right;     // 返回旧root的右孩子作为新root
                return root;
            }
        }
        if (root.val > key) 
            root.left = deleteNode(root.left, key);
        if (root.val < key) 
            root.right = deleteNode(root.right, key);
        return root;
    }
}

解法二：迭代

删除节点的迭代法还是复杂一些的，但其本质我在递归法里都介绍了，最关键就是删除节点的操作

class Solution {
    // 将目标节点（删除节点）的左子树放到 目标节点的右子树的最左面节点的左孩子位置上
    // 并返回目标节点右孩子为新的根节点
    // 是动画里模拟的过程
    public TreeNode deleteOneNode(TreeNode target) {
        if (target == null) 
            return target;
        if (target.right == null) 
            return target.left;
        TreeNode cur = target.right;
        while (cur.left) {
            cur = cur.left;
        }
        cur.left = target.left;
        return target.right;
    }

    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) 
            return root;
        TreeNode cur = root;
        TreeNode pre = null; // 记录cur的父节点，用来删除cur
        while (cur) {
            if (cur.val == key) 
                break;
            pre = cur;
            if (cur.val > key) 
                cur = cur.left;
            else cur = cur.right;
        }
        if (pre == null) { // 如果搜索树只有头结点
            return deleteOneNode(cur);
        }
        // pre 要知道是删左孩子还是右孩子
        if (pre.left && pre.left.val == key) {
            pre.left = deleteOneNode(cur);
        }
        if (pre.right && pre.right.val == key) {
            pre.right = deleteOneNode(cur);
        }
        return root;
    }
}