问题

给两个整数数组 A 和 B，返回两个数组中公共的、长度最长的子数组的长度

示例：

输入：
A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出：3
解释：
长度最长的公共子数组是 [3, 2, 1]

思路

注意题目中说的子数组，其实就是连续子序列。这种问题动规最拿手，动规五部曲分析如下：

  • 确定dp数组以及下标的含义

    • dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]
    • 那dp[0][0]是什么含义呢？总不能是以下标-1为结尾的A数组吧
      • 其实dp[i][j]的定义也就决定着，我们在遍历dp[i][j]的时候i和j都要从1开始
    • 如果定义dp[i][j]为以下标i为结尾的A，和以下标j为结尾的B，最长重复子数组长度。不行么？行倒是行！但实现起来就麻烦了一些

  • 确定递推公式

    • 根据dp[i][j]的定义，dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来
    • 即当A[i - 1]和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1;

  • dp数组如何初始化

    • 根据dp[i][j]的定义，dp[i][0]和dp[0][j]其实都是没有意义的！
    • 但dp[i][0]和dp[0][j]要初始值，因为为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;
    • 所以dp[i][0]和dp[0][j]初始化为0
      • 举个例子A[0]如果和B[0]相同的话，dp[1][1] = dp[0][0] + 1，只有dp[0][0]初始为0，正好符合递推公式逐步累加起来

  • 确定遍历顺序

    • 外层for循环遍历A，内层for循环遍历B
    • 同时题目要求长度最长的子数组的长度。所以在遍历的时候顺便把dp[i][j]的最大值记录下来
      1. for (int i = 1; i <= A.length; i++) {
      2. for (int j = 1; j <= B.length; j++) {
      3.    if (A[i - 1] == B[j - 1]) {
      4.        dp[i][j] = dp[i - 1][j - 1] + 1;
      5.    }
      6.    if (dp[i][j] > result) 
      7.        result = dp[i][j];
      8. }
      9. }

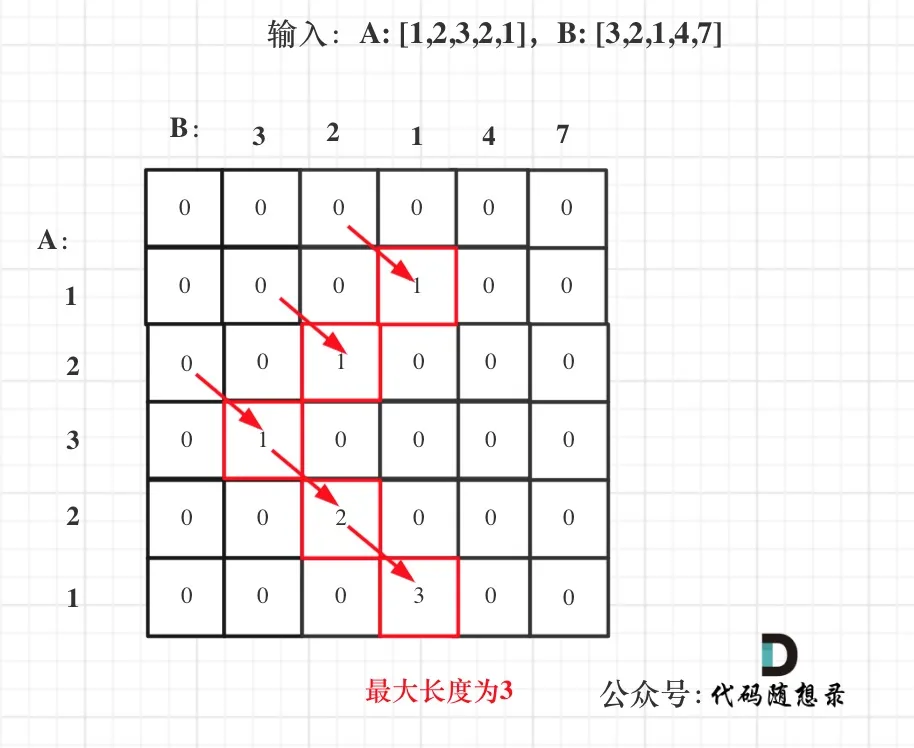
  • 举例推导dp数组

    • 拿示例1中，A: [1,2,3,2,1]，B: [3,2,1,4,7]为例，画一个dp数组的状态变化，如下：

640 (2).webp

  1. class Solution {
  2.     public int findLength(int[] A, int[] B) {
  3.         int[][] dp = new int[A.length + 1][B.length + 1];
  5.         int result = 0;
  7.         for (int i = 1; i <= A.length; i++) {
  8.             for (int j = 1; j <= B.length; j++) {
  9.                 if (A[i - 1] == B[j - 1]) {
  10.                     dp[i][j] = dp[i - 1][j - 1] + 1;
  11.                 }
  12.                 if (dp[i][j] > result) 
  13.                     result = dp[i][j];
  14.             }
  15.         }
  16.         return result;
  17.     }
  18. }
  • 时间复杂度：leetcode-718：最长重复子数组 - 图2，n为A长度，m为B长度
  • 空间复杂度：leetcode-718：最长重复子数组 - 图3