问题
编写一个算法来判断一个数 n 是不是快乐数
快乐数定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和
- 重复这个过程直到这个数变为 1,也可能是无限循环但始终变不到 1
- 如果可以变为1,那么这个数就是快乐数;如果 n 是快乐数就返回 true ;不是,则返回 false
示例 1:输入:19 输出:true
示例 2:输入:n = 2 输出:false
方法一:用哈希集合检测循环
从 116 开始,通过反复平方和计算下一个数字,最终得到 58,再继续计算之后,又回到 58。由于我们回到了一个已经计算过的数字,可以知道有一个循环,因此不可能达到 1。所以对于 116,函数应该返回 false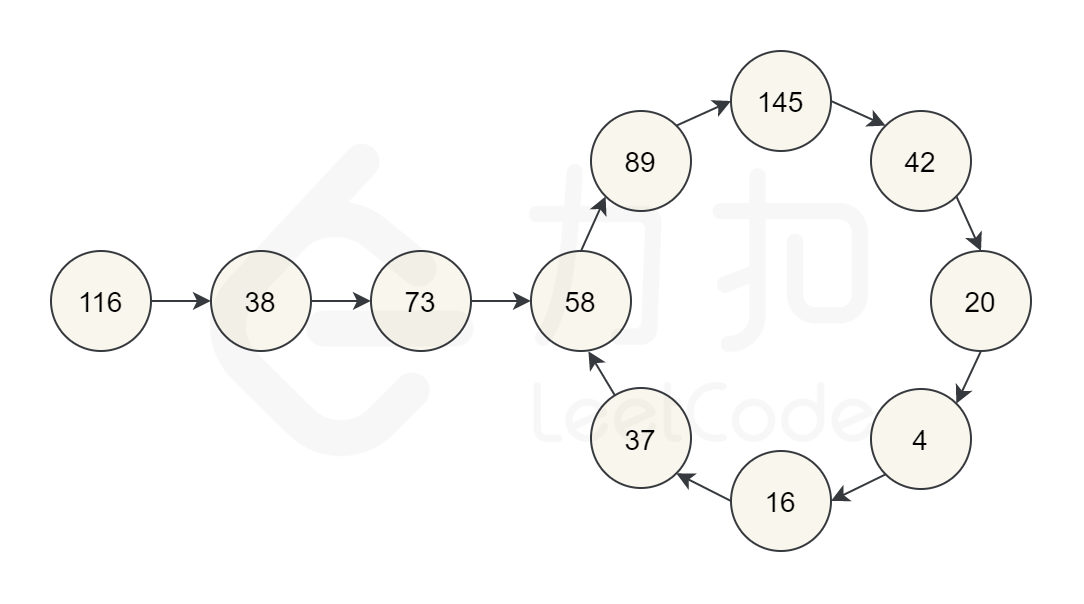
因此在求解快乐数的过程中可能会存在以下三种情况:
- 1
- 循环
- 值趋于无穷大
趋于无穷大的情况难以检测和处理。我们怎么知道它会继续变大,而不是最终得到 1 呢?我们可以仔细想一想,每一位数的最大数字的下一位数是多少。
| Digits | Largest | Next |
|---|---|---|
| 1 | 9 | 81 |
| 2 | 99 | 162 |
| 3 | 999 | 243 |
| 4 | 9999 | 324 |
| 5 | 99999 | 405 |
| 6 | 999999 | 486 |
对于 3 位数的数字,它不可能大于 243。这意味着它要么被困在 243 以下的循环内,要么跌到 1;4 位或 4 位以上的数字在每一步都会丢失一位,直到降到 3 位为止。所以,最坏的情况下,算法可能会在 243 以下的所有数字上循环,然后回到它已经到过的一个循环或者回到 1。但它不会无限期地进行下去,所以排除第三种选择
算法分为两部分,我们需要设计和编写代码
- 给一个数字 n,它的下一个数字是什么
- 我们按照题目的要求做数位分离,求平方和
- 按照一系列的数字来判断我们是否进入了一个循环
- 可以使用哈希集合完成。每次生成链中的下一个数字时,我们都会检查它是否已经在哈希集合中
- 如果它不在哈希集合中,我们应该添加它
- 如果它在哈希集合中,这意味着我们处于一个循环中,因此应该返回 false
- 可以使用哈希集合完成。每次生成链中的下一个数字时,我们都会检查它是否已经在哈希集合中
我们使用哈希集合而不是向量、列表或数组的原因是因为我们反复检查其中是否存在某数字
检查数字是否在哈希集合中需要的时间,而对于其他数据结构,则需要
的时间。选择正确的数据结构是解决这些问题的关键部分
package leetcode;import java.util.HashSet;import java.util.Set;public class leetcode_202 {private int getNext(int n){//公共成员用public来修饰,可以被所有类访问//私有成员用private来修饰,它只允许在自己类的内部被访问int totalSum = 0;while(n > 0){int d = n % 10;n = n / 10;totalSum += d * d;}return totalSum;}public boolean isHappy(int n){Set<Integer> seen = new HashSet<>();while (n != 1 && !seen.contains(n)) {//.contains 用于判断list集合是否包含某个元素seen.add(n);n = getNext(n);}return n == 1;}}
- 时间复杂度:
- 空间复杂度:
方法二:快慢指针
通过反复调用 getNext(n) 得到的链是一个隐式的链表。隐式意味着我们没有实际的链表节点和指针,但数据仍然形成链表结构。起始数字是链表的头 “节点”,链中的所有其他数字都是节点。next 指针通过调用 getNext(n) 函数获得
意识到我们实际有个链表,那么这个问题就可以转换为检测一个链表是否有环。因此我们在这里可以使用弗洛伊德循环查找算法
我们不是只跟踪链表中的一个值,而是跟踪两个值,即快慢指针。在算法的每一步中,慢指针在链表中前进 1 个节点,快指针前进 2 个节点(对getNext(n)函数的嵌套调用)
- 如果 n 是一个快乐数,即没有循环,那么快跑者最终会比慢跑者先到达数字 1
如果 n 不是一个快乐的数字,那么最终快跑者和慢跑者将在同一个数字上相遇
class Solution {public int getNext(int n) {int totalSum = 0;while (n > 0) {int d = n % 10;n = n / 10;totalSum += d * d;}return totalSum;}public boolean isHappy(int n) {int slowRunner = n;int fastRunner = getNext(n);while (fastRunner != 1 && slowRunner != fastRunner) {slowRunner = getNext(slowRunner);fastRunner = getNext(getNext(fastRunner));}return fastRunner == 1;}}
时间复杂度:
- 空间复杂度:

