leetcode-459：重复的子字符串

问题

给定一个非空的字符串，判断它是否可以由它的一个子串重复多次构成。给定的字符串只含有小写英文字母，并且长度不超过10000

示例 1:
输入: “abab”
输出: True

解释: 可由子字符串 “ab” 重复两次构成

示例 2:
输入: “aba”
输出: False

示例 3:
输入: “abcabcabcabc”
输出: True

解释: 可由子字符串 “abc” 重复四次构成。 (或者子字符串 “abcabc” 重复两次构成。)

思路

这里就要说一说next数组了，next 数组记录的就是最长相同前后缀，如果next[len - 1] != -1，则说明字符串有最长相同的前后缀（就是字符串里的前缀子串和后缀子串相同的最长长度）

• 最长相等前后缀的长度为：next[len - 1] + 1
• 数组长度为：len

如果len % (len - (next[len - 1] + 1)) == 0，则说明 (数组长度-最长相等前后缀的长度) 正好可以被数组的长度整除，说明有该字符串有重复的子字符串
强烈建议大家把next数组打印出来，看看next数组里的规律，有助于理解KMP算法

如图：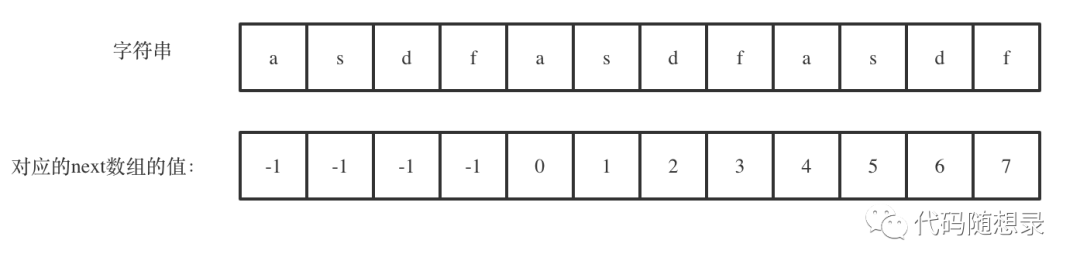

此时next[len - 1] = 7，next[len - 1] + 1 = 8，8就是此时 字符串asdfasdfasdf的最长相同前后缀的长度。(len - (next[len - 1] + 1)) 也就是：12(字符串的长度) - 8(最长公共前后缀的长度) = 4， 4正好可以被 12(字符串的长度) 整除，所以说明有重复的子字符串（asdf）

解法一：KMP

package leetcode_459;
import java.util.Arrays;
public class solution {
    public boolean repeatedSubstringPattern(String s) {
        return kmp(s);
    }
    public boolean kmp(String pattern){
        int length = pattern.length();
        int[] a = new int[length];
        Arrays.fill(a, -1);
        for(int i = 1; i < length; i++){
            int j = a[i - 1];
            while(j != -1 && pattern.charAt(j + 1) != pattern.charAt(i)){
                j = a[j];
            }
            if(pattern.charAt(j + 1) == pattern.charAt(i)){
                a[i] = j + 1;
            }
        }
        return a[length - 1] != -1 && length % (length - a[length - 1] - 1) == 0;
    }
}

• 时间复杂度：
• 空间复杂度：

方法二：枚举

如果一个长度为n的字符串s可以由它的一个长度为n'的子串s' 重复多次构成，那么：

• n一定是n'的倍数
• s'一定是s的前缀
• 对于任意的，有

也就是说，s中长度为n'的前缀就是s'，并且在这之后的每一个位置上的字符s[i]，都需要与它之前的第n'个字符s[i-n']相同
因此，我们可以从小到大枚举n'，并对字符串s进行遍历，进行上述的判断。注意到一个小优化是，因为子串至少需要重复一次，所以n'不会大于n的一半，我们只需要在的范围内枚举n'即可

class Solution {
    public boolean repeatedSubstringPattern(String s) {
        int n = s.length();
        for (int i = 1; i * 2 <= n; ++i) {
            if (n % i == 0) {
                boolean match = true;
                for (int j = i; j < n; ++j) {
                    if (s.charAt(j) != s.charAt(j - i)) {
                        match = false;
                        break;
                    }
                }
                if (match) {
                    return true;
                }
            }
        }
        return false;
    }
}