问题

根据一棵树的中序遍历与后序遍历构造二叉树
注意:
你可以假设树中没有重复的元素

例如，给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树：

  1. 3<br />   / \<br />  9  20<br />    /  \<br />   15   7

解法一：递归

以后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来在切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素

流程如图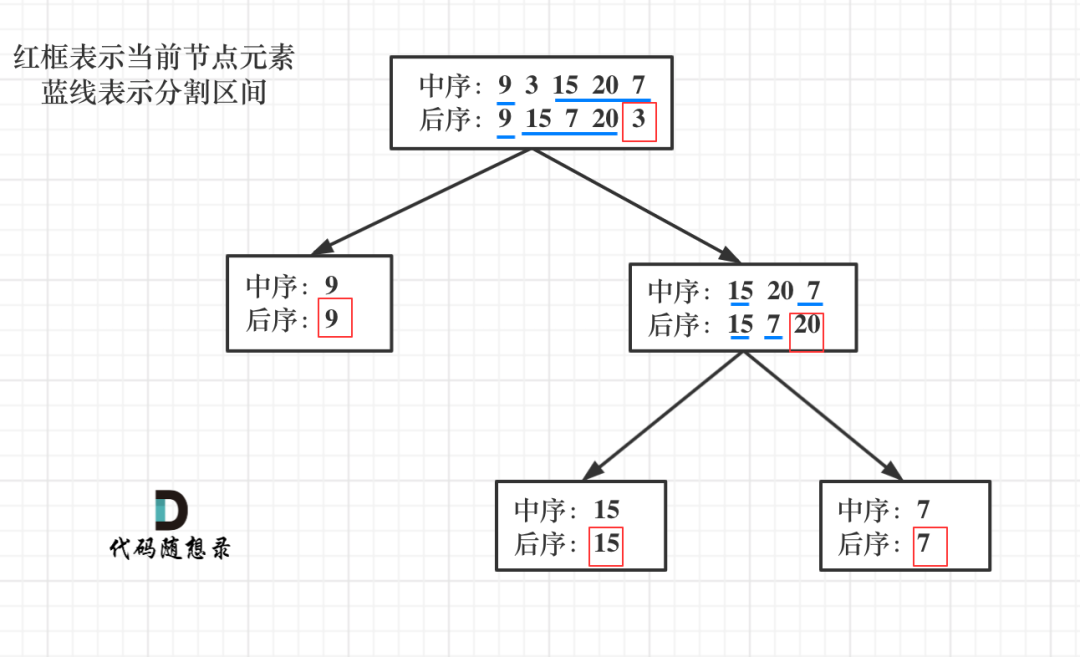：leetcode-106：从中序与后序遍历序列构造二叉树 - 图1
说到一层一层切割，就应该想到了递归

来看一下一共分几步：

  • 第一步：如果数组大小为零的话，说明是空节点了
  • 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素
  • 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
  • 第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
  • 第五步：切割后序数组，切成后序左数组和后序右数组
  • 第六步：递归处理左区间和右区间

算法

  • 为了高效查找根节点元素在中序遍历数组中的下标，我们选择创建哈希表来存储中序序列，即建立一个（元素，下标）键值对的哈希表

  • 定义递归函数 helper(in_left, in_right) 表示当前递归到中序序列中当前子树的左右边界，递归入口为helper(0, n - 1) ：

    • 如果 in_left > in_right，说明子树为空，返回空节点
    • 选择后序遍历的最后一个节点作为根节点
    • 利用哈希表 O(1) 查询当根节点在中序遍历中下标为 index。从 in_left 到 index - 1 属于左子树，从 index + 1 到 in_right 属于右子树
    • 根据后序遍历逻辑，递归创建右子树 helper(index + 1, in_right) 和左子树 helper(in_left, index - 1)。注意这里有需要先创建右子树，再创建左子树的依赖关系。可以理解为在后序遍历的数组中整个数组是先存储左子树的节点，再存储右子树的节点，最后存储根节点，如果按每次选择后序遍历的最后一个节点为根节点，则先被构造出来的应该为右子树

    • 返回根节点 root

      1. class Solution {
      2. int post_idx;
      3. int[] postorder;
      4. int[] inorder;
      5. Map<Integer, Integer> idx_map = new HashMap<Integer, Integer>();
      7. public TreeNode helper(int in_left, int in_right) {
      8.    // 如果这里没有节点构造二叉树了，就结束
      9.    if (in_left > in_right) {
      10.        return null;
      11.    }
      13.    // 选择 post_idx 位置的元素作为当前子树根节点
      14.    int root_val = postorder[post_idx];
      15.    TreeNode root = new TreeNode(root_val);
      17.    // 根据 root 所在位置分成左右两棵子树
      18.    int index = idx_map.get(root_val);
      20.    // 下标减一
      21.    post_idx--;
      22.    // 构造右子树
      23.    root.right = helper(index + 1, in_right);
      24.    // 构造左子树
      25.    root.left = helper(in_left, index - 1);
      26.    return root;
      27. }
      29. public TreeNode buildTree(int[] inorder, int[] postorder) {
      30.    this.postorder = postorder;
      31.    this.inorder = inorder;
      32.    // 从后序遍历的最后一个元素开始
      33.    post_idx = postorder.length - 1;
      35.    // 建立（元素，下标）键值对的哈希表
      36.    int idx = 0;
      37.    for (Integer val : inorder) {
      38.        idx_map.put(val, idx++);
      39.    }
      41.    return helper(0, inorder.length - 1);
      42. }
      43. }

  • 时间复杂度：leetcode-106：从中序与后序遍历序列构造二叉树 - 图2，n是树中的节点个数

  • 空间复杂度：leetcode-106：从中序与后序遍历序列构造二叉树 - 图3。我们需要使用 leetcode-106：从中序与后序遍历序列构造二叉树 - 图4 的空间存储哈希表，以及 leetcode-106：从中序与后序遍历序列构造二叉树 - 图5（其中 h 是树的高度）的空间表示递归时栈空间。这里 h < n，所以总空间复杂度为 leetcode-106：从中序与后序遍历序列构造二叉树 - 图6

解法二：迭代法

leetcode官解