问题

给定一个二叉树，找出其最小深度
最小深度是从根节点到最近叶子节点的最短路径上的节点数量
说明：叶子节点是指没有子节点的节点

示例 1：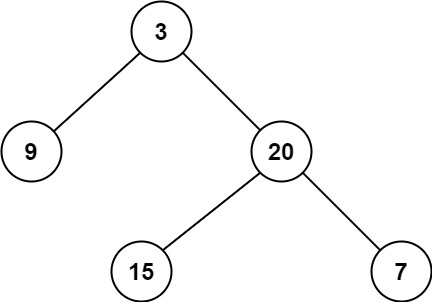
leetcode-111：二叉树的最小深度 - 图1
输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

思路

在求解树的最大深度和最小深度，直觉上好像是差不多的，其实还是差不少的
最大深度很容易理解，最小深度可有一个误区，如图：
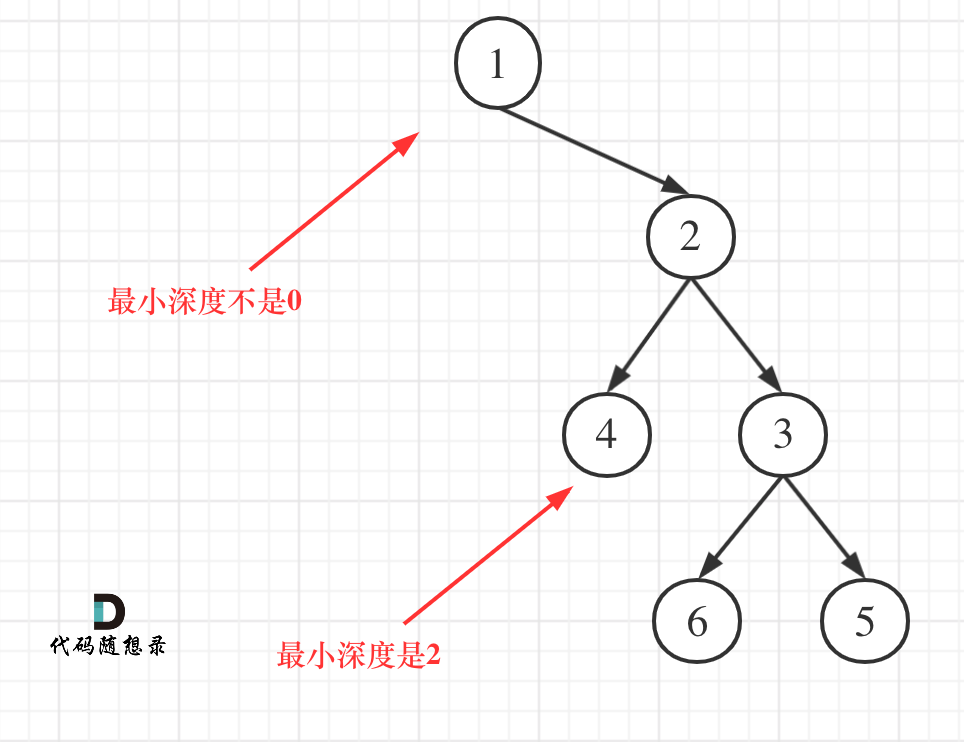
leetcode-111：二叉树的最小深度 - 图2
这就重新审题了，题目中说的是：最小深度是从根节点到最近叶子节点的最短路径上的节点数量。注意是叶子节点
而左右孩子都为空的节点才是叶子节点

解法一：递归法

递归三部曲：

  • 确定递归函数的参数和返回值

    • 参数为要传入的二叉树根节点，返回的是int类型的深度。
      1. int getDepth(TreeNode node)

  • 确定终止条件

    • 终止条件也是遇到空节点返回0，表示当前节点的高度为0
      1. if (node == NULL) return 0;

  • 确定单层递归的逻辑

    • 这块和求最大深度可就不一样了，一些同学可能会写如下代码：
      1. int leftDepth = getDepth(node.left);
      2. int rightDepth = getDepth(node.right);
      3. int result = 1 + Math.min(leftDepth, rightDepth);
      4. return result;
      这个代码就犯了此图中的误区：
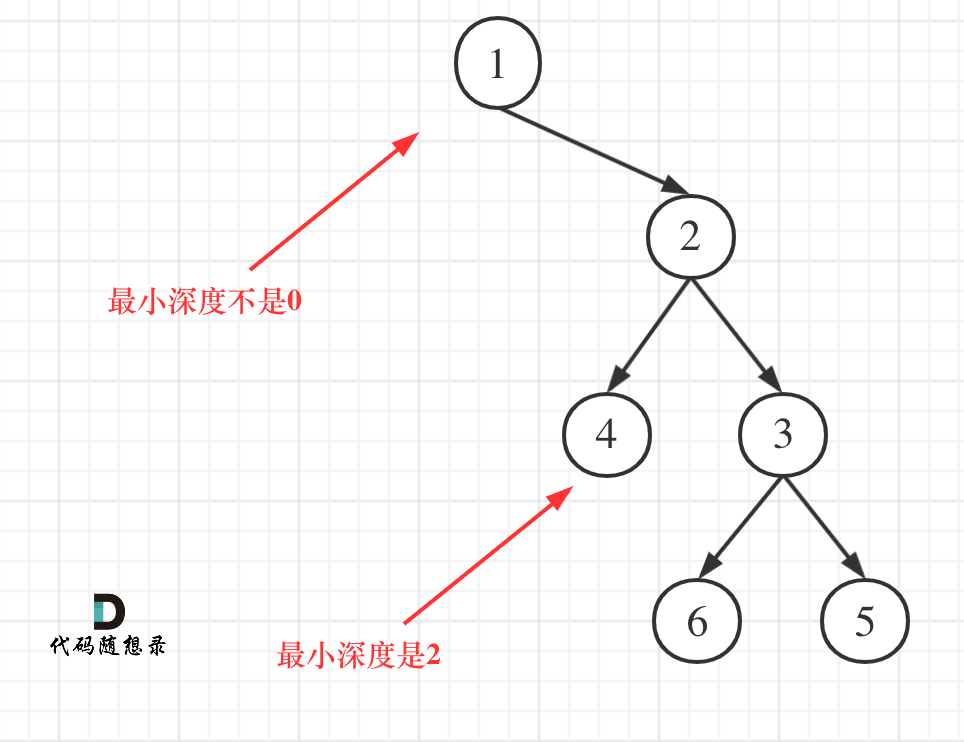
      leetcode-111：二叉树的最小深度 - 图3
      如果这么求的话，没有左孩子的分支会算为最短深度

  • 所以，如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度

  • 反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。最后如果左右子树都不为空，返回左右子树深度最小值 + 1 

    1. //官解：分别计算左右子树最小叶子节点的深度
    2. class Solution {
    3.   public int minDepth(TreeNode root) {
    4.       if (root == null) {
    5.           return 0;
    6.       }
    8.       if (root.left == null && root.right == null) {
    9.           return 1;
    10.       }
    12.       int min_depth = Integer.MAX_VALUE;
    13.       if (root.left != null) {
    14.           min_depth = Math.min(minDepth(root.left), min_depth);
    15.       }
    16.       if (root.right != null) {
    17.           min_depth = Math.min(minDepth(root.right), min_depth);
    18.       }
    20.       return min_depth + 1;
    21.   }
    22. }
    1. class Solution {
    2.   public int minDepth(TreeNode root) {
    3.       return getDepth(root);
    4.   }
    6.   public int getDepth(TreeNode root){
    7.       if (root == null){
    8.           return 0;
    9.       }
    11.       int leftDepth = getDepth(root.left);    // 左
    12.       int rightDepth = getDepth(root.right);  // 右
    13.                                                // 中
    14.       // 当一个左子树为空，右不为空，这时并不是最低点
    15.       if (root.left == null && root.right != null) { 
    16.           return 1 + rightDepth;
    17.       }   
    18.       // 当一个右子树为空，左不为空，这时并不是最低点
    19.       if (root.left != null && root.right == null) { 
    20.           return 1 + leftDepth;
    21.       }
    22.       int result = 1 + Math.min(leftDepth, rightDepth); 
    23.       return result;
    24.   }
    25. }

解法二：广度优先遍历

  1. //自解
  2. class Solution{
  3.     public int minDepth(TreeNode root) {
  4.         if (root == null) {
  5.             return 0;
  6.         }
  7.         Deque<TreeNode> deque = new LinkedList<>();
  8.         deque.offer(root);
  9.         int level = 1;
  10.         while (!deque.isEmpty()) {
  11.             int size = deque.size();
  12.             for (int i = 0; i < size; i++) {
  13.                 TreeNode cur = deque.poll();
  14.                 if (cur.right == null && cur.left == null){
  15.                     return level;
  16.                 }
  17.                 if (cur.left != null){
  18.                     deque.offer(cur.left);
  19.                 }
  20.                 if (cur.right != null){
  21.                     deque.offer(cur.right);
  22.                 }
  23.             }
  24.             level++;
  25.         }
  26.         return level;
  27.     }
  28. }
  1. //官解
  2. class Solution {
  3.     class QueueNode {
  4.         TreeNode node;
  5.         int depth;
  7.         public QueueNode(TreeNode node, int depth) {
  8.             this.node = node;
  9.             this.depth = depth;
  10.         }
  11.     }
  13.     public int minDepth(TreeNode root) {
  14.         if (root == null) {
  15.             return 0;
  16.         }
  18.         Queue<QueueNode> queue = new LinkedList<QueueNode>();
  19.         queue.offer(new QueueNode(root, 1));
  20.         while (!queue.isEmpty()) {
  21.             QueueNode nodeDepth = queue.poll();
  22.             TreeNode node = nodeDepth.node;
  23.             int depth = nodeDepth.depth;
  24.             if (node.left == null && node.right == null) {
  25.                 return depth;
  26.             }
  27.             if (node.left != null) {
  28.                 queue.offer(new QueueNode(node.left, depth + 1));
  29.             }
  30.             if (node.right != null) {
  31.                 queue.offer(new QueueNode(node.right, depth + 1));
  32.             }
  33.         }
  35.         return 0;
  36.     }
  37. }
  39. 作者：LeetCode-Solution
  40. 链接：https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/solution/er-cha-shu-de-zui-xiao-shen-du-by-leetcode-solutio/
  41. 来源：力扣（LeetCode）
  42. 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
  • 时间复杂度：leetcode-111：二叉树的最小深度 - 图4，其中 N 是树的节点数。对每个节点访问一次
  • 空间复杂度：leetcode-111：二叉树的最小深度 - 图5，其中 N 是树的节点数。空间复杂度主要取决于队列的开销，队列中的元素个数不会超过树的节点数