leetcode-429：N叉树的层序遍历

问题

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）
树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）

示例 1：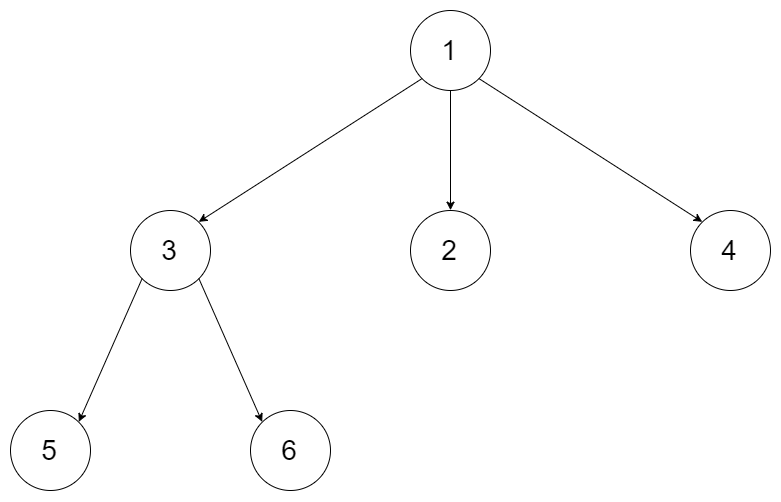

输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

示例 2：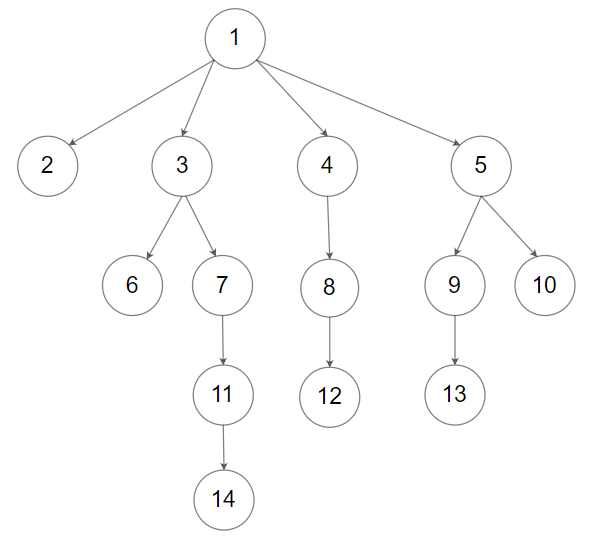

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

解法一：自解

class Solution {
    public List<List<Integer>> levelOrder(Node root) {      
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        Queue<Node> queue = new LinkedList<Node>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            List<Integer> level = new ArrayList<Integer>();
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                Node node = queue.poll();    
                level.add(node.val);
                queue.addAll(node.children);
            }
            res.add(level);
        }
        return res;
    }
}

• 时间复杂度：。n 指的是节点的数量
• 空间复杂度：

解法二：递归

我们可以使用递归来解决这个问题，通常我们不能使用递归进行广度优先搜索。这是因为广度优先搜索基于队列，而递归运行时使用堆栈，适合深度优先搜索。但是在本题中，我们可以以不同的顺序添加到最终列表中，只要我们知道节点在哪一层并确保在那一层的列表顺序正确就可以了

class Solution {
    private List<List<Integer>> result = new ArrayList<>();
    public List<List<Integer>> levelOrder(Node root) {
        if (root != null) traverseNode(root, 0);
        return result;
    }
    private void traverseNode(Node node, int level) {
        if (result.size() <= level) {
            result.add(new ArrayList<>());
        }
        result.get(level).add(node.val);
        for (Node child : node.children) {
            traverseNode(child, level + 1);
        }
    }
}