问题

给你一个二进制字符串数组 strs 和两个整数 m 和 n
请你找出并返回 strs 的最大子集的大小，该子集中最多有 m 个 0 和 n 个 1
如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的子集

示例 1：
输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,”0001”,”1”,”0”} ，因此答案是 4
其他满足题意但较小的子集包括 {“0001”,”1”} 和 {“10”,”1”,”0”} 。{“111001”} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3

示例 2：
输入：strs = ["10", "0", "1"], m = 1, n = 1
输出：2
解释：最大的子集是 {“0”, “1”} ，所以答案是 2

思路

本题可能会认为是多重背包，一些题解也是这么写的
其实本题并不是多重背包，再来看一下这个图，捋清几种背包的关系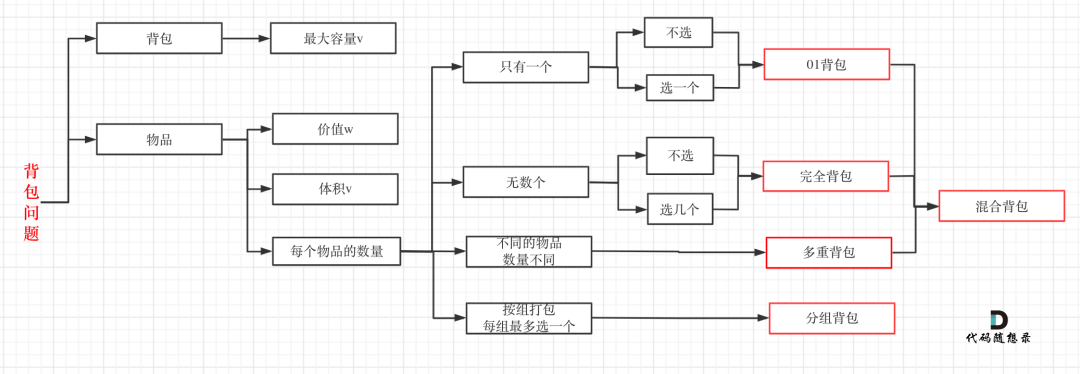
640 (2).png
多重背包是每个物品，数量不同的情况

本题中**strs**数组里的元素就是物品，每个物品都是一个！
而**m**和**n**相当于是一个背包，两个维度的背包

理解成多重背包主要是把m和n混淆为物品了，感觉这是不同数量的物品，所以以为是多重背包
但本题其实是01背包问题！
这不过这个背包有两个维度，一个是m一个是n，而不同长度的字符串就是不同大小的待装物品

  • 确定dp数组（dp table）以及下标的含义

    • dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]

  • 确定递推公式

    • dp[i][j]可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1
    • dp[i][j]就可以是 dp[i - zeroNum][j - oneNum] + 1，然后我们在遍历的过程中，取dp[i][j]的最大值
    • 所以递推公式：dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

回想一下01背包的递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
对比一下就会发现，字符串的zeroNum和oneNum相当于物品的重量（weight[i]），字符串本身的个数相当于物品的价值（value[i]）
这就是一个典型的01背包！ 只不过物品的重量有了两个维度而已

  • dp数组如何初始化

    • 01背包的dp数组初始化为0就可以。因为物品价值不会是负数，初始为0，保证递推的时候dp[i][j]不会被初始值覆盖

  • 确定遍历顺序

    • 外层for循环遍历物品，内层for循环遍历背包容量且从后向前遍历

    • 那么本题也是，物品就是strs里的字符串，背包容量就是题目描述中的m和n。

      1. for (String str : strs) { // 遍历物品
      2. int oneNum = 0, zeroNum = 0;
      4. for (char ch : str.toCharArray()) {
      5.    if (ch == '0') 
      6.        zeroNum++;
      7.    else oneNum++;
      8. }
      9. for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历！
      10.    for (int j = n; j >= oneNum; j--) {
      11.        dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
      12.    }
      13. }
      14. }

      先遍历那个都行！

  • 举例推导dp数组

以输入：[“10”,”0001”,”111001”,”1”,”0”]，m = 3，n = 3为例
最后dp数组的状态如下所示：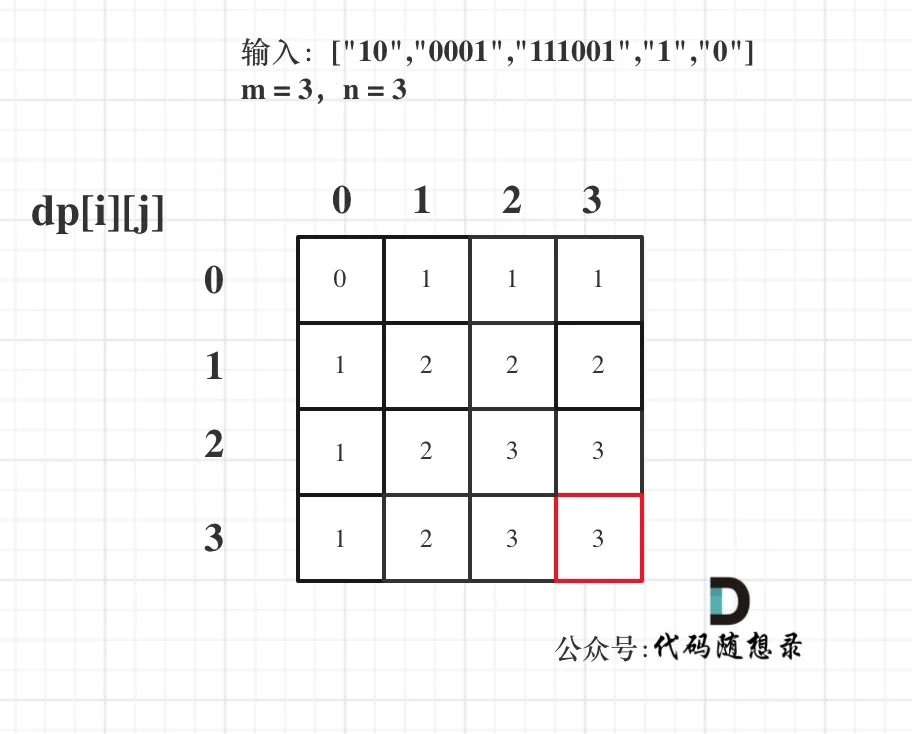
640 (1).webp

  1. class Solution {
  2.     public int findMaxForm(String[] strs, int m, int n) {
  3.         //dp[i][j]表示i个0和j个1时的最大子集
  4.         int[][] dp = new int[m + 1][n + 1];
  5.         int oneNum, zeroNum;
  6.         for (String str : strs) {
  7.             oneNum = 0;
  8.             zeroNum = 0;
  9.             for (char ch : str.toCharArray()) {
  10.                 if (ch == '0') {
  11.                     zeroNum++;
  12.                 } else {
  13.                     oneNum++;
  14.                 }
  15.             }
  16.             //倒序遍历
  17.             for (int i = m; i >= zeroNum; i--) {
  18.                 for (int j = n; j >= oneNum; j--) {
  19.                     dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
  20.                 }
  21.             }
  22.         }
  23.         return dp[m][n];
  24.     }
  25. }

for-each语句针对于集合元素