1. public class Solution {
  2.     LinkedList<Integer> path = new LinkedList<Integer>(); // 用来存放符合条件单一结果
  3.     List<List<Integer>> result = new ArrayList<List<Integer>>(); // 存放符合条件结果的集合
  5.     public List<List<Integer>> combine(int n, int k) {
  6.         if (k <= 0 || n < k) {
  7.             return result;
  8.         }
  9.         backtracking(n, k, 1);
  10.         return result;
  11.     }
  13.     public void backtracking(int n, int k, int startIndex) {
  14.         // 递归终止条件是：path 的长度等于 k
  15.         if (path.size() == k) {
  16.                 result.add(new LinkedList<Integer>(path));
  17.             return;
  18.         }
  20.         // 遍历可能的搜索起点
  21.         for (int i = startIndex; i <= n; i++) { // 控制树的横向遍历
  22.         // 向路径变量里添加一个数 
  23.         path.addLast(i); 
  24.         // 递归：控制树的纵向遍历
  25.         backtracking(n, k, i + 1); 
  26.         // 回溯
  27.         path.removeLast(); 
  28.         }
  29.     }
  30. }

来举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。在第二层for循环，从元素3开始的遍历都没有意义了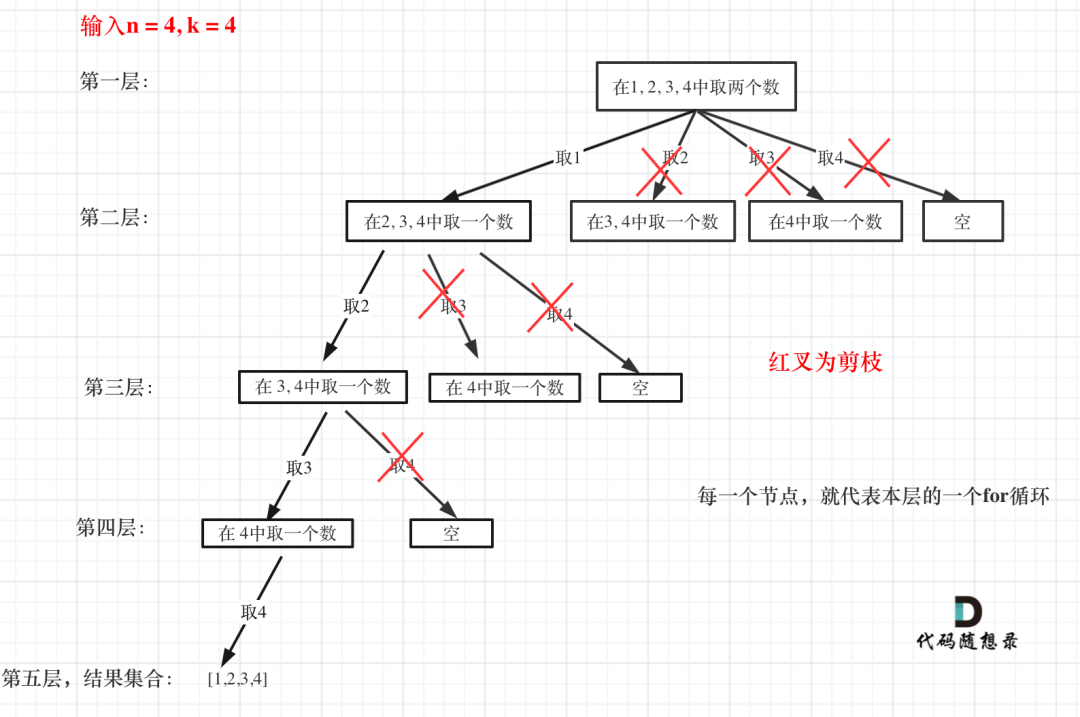
leetcode-77：组合 剪枝 - 图1
所以，可以剪枝的地方就在递归中每一层的**for**循环所选择的起始位置
如果**for**循环选择的起始位置之后的元素个数已经不足我们需要的元素个数了，那么就没有必要搜索了

优化过程

  • 已经选择的元素个数：path.size();
  • 还需要的元素个数为: k - path.size();
  • 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

举个例子，n = 4，k = 3， 目前已经选取的元素为0，n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2
从2开始搜索都是合理的，可以是组合[2, 3, 4]

  1. for(int i = startIndex; i <= n - (k - path.size()) + 1; i++)