问题

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次

说明：
所有数字（包括目标数）都是正整数
解集不能包含重复的组合

示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]

示例 2:
输入: candidates = [2,5,2,1,2], target = 5
所求解集为:
[
[1,2,2],
[5]
]

思路

这道题目和leetcode-39：求组合总和如下区别：

  1. 本题candidates中的每个数字在每个组合中只能使用一次
  2. 本题数组candidates的元素是有重复的，而之前是无重复元素的数组candidates

最后本题要求解集不能包含重复的组合

本题的难点在于：集合（数组candidates）有重复元素，但还不能有重复的组合

我们需要在搜索的过程中就去掉重复组合
所谓去重，其实就是使用过的元素不能重复选取
都知道组合问题可以抽象为树形结构，那么“使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上使用过，一个维度是同一树层上使用过。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因

那么问题来了，我们是要同一树层上使用过，还是同一树枝上使用过呢？
回看一下题目，元素在同一个组合内是可以重复的，怎么重复都没事，但两个组合不能相同
所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重

为了理解去重我们来举一个例子，candidates = [1, 1, 2], target = 3，（方便起见candidates已经排序了）
选择过程树形结构如图所示：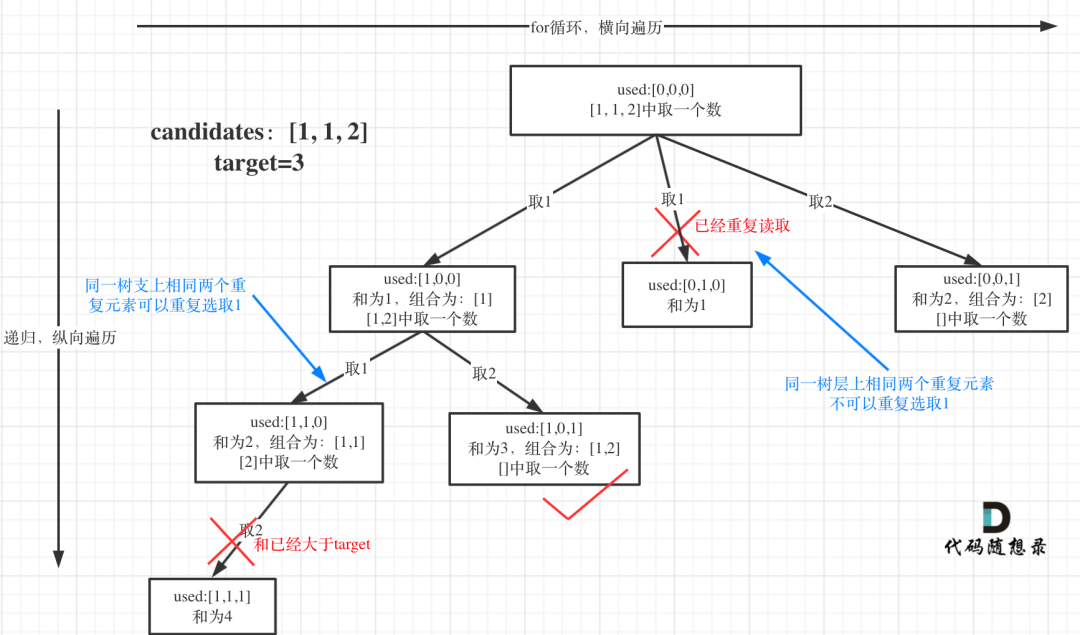
leetcode-40：组合总和Ⅱ - 图1
可以看到图中，每个节点相对于leetcode-39：求组合总和多加了used数组

回溯三部曲

  • 递归函数参数

    • 此题还需要加一个bool型数组used，用来记录同一树枝上的元素是否使用过
      1. List<List<Integer>> result = new ArrayList<List<Integer>>(); // 存放组合集合
      2. List<Integer> path = new ArrayList<Integer>();           // 符合条件的组合
      3. public void backtracking(int[] candidates, int target, int sum, int startIndex, boolean[] used)

  • 递归终止条件

    1. if (sum > target) { // 这个条件其实可以省略 
    2.   return;
    3. }
    4. if (sum == target) {
    5.   result.add(new ArrayList<Integer>(path));
    6.   return;
    7. }

  • 单层搜索的逻辑

    • 这里最需要注意的地方就是去重
      • 前面我们提到：要去重的是“同一树层上的使用过”，如何判断同一树层上元素（相同的元素）是否使用过了呢

如果**candidates[i] == candidates[i - 1]** 并且 **used[i - 1] == false**，就说明：前一个树枝，使用了**candidates[i - 1]**，也就是说同一树层使用过**candidates[i - 1]**
此时for循环里就应该做continue的操作
这块比较抽象，如图：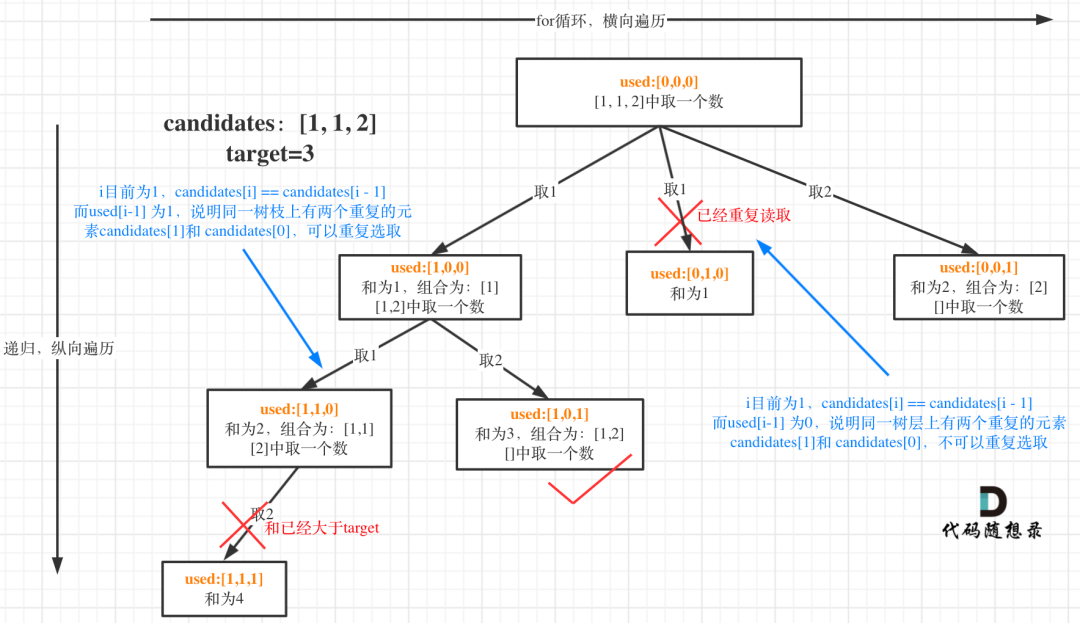
leetcode-40：组合总和Ⅱ - 图2
我在图中将used的变化用橘黄色标注上，可以看出在candidates[i] == candidates[i - 1]相同的情况下：

  • used[i - 1] == true，说明同一树支candidates[i - 1]使用过

  • used[i - 1] == false，说明同一树层candidates[i - 1]使用过

    1. for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) {
    3.   if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
    4.       continue;
    5.   }
    6.   sum += candidates[i];
    7.   path.add(candidates[i]);
    8.   used[i] = true;
    9.   backtracking(candidates, target, sum, i + 1, used); 
    10.   used[i] = false;
    11.   sum -= candidates[i];
    12.   path.remove(path.size() - 1);
    13. }
    1. class Solution {
    2.   List<List<Integer>> result = new ArrayList<List<Integer>>(); // 存放组合集合
    3.   List<Integer> path = new ArrayList<Integer>();           // 符合条件的组合
    5.   public void backtracking(int[] candidates, int target, int sum, int startIndex, boolean[] used){
    6.       if (sum == target) {
    7.           result.add(new ArrayList<Integer>(path)); 
    8.           //Java默认传引用，将path变量中的元素放入result中，需要重新new一个
    9.           return;
    10.       }
    12.       for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) {
    13.           if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
    14.           continue;
    15.           }
    17.           sum += candidates[i];
    18.           path.add(candidates[i]);
    19.           used[i] = true;
    20.           backtracking(candidates, target, sum, i + 1, used); 
    21.           used[i] = false;
    22.           sum -= candidates[i];
    23.           path.remove(path.size() - 1);
    24.   }
    25.   }
    27.   public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    28.       boolean[] used = new boolean[candidates.length];
    30.       // 首先把给candidates排序，让其相同的元素都挨在一起。
    31.       Arrays.sort(candidates);
    32.       backtracking(candidates, target, 0, 0, used);
    33.       return result;
    34.   }
    35. }


    官解

    ```java import java.util.ArrayDeque; import java.util.ArrayList; import java.util.Arrays; import java.util.Deque; import java.util.List;

public class Solution {

  1. public List<List<Integer>> combinationSum2(int[] candidates, int target) {
  2.     int len = candidates.length;
  3.     List<List<Integer>> res = new ArrayList<>();
  4.     if (len == 0) {
  5.         return res;
  6.     }
  8.     // 关键步骤
  9.     Arrays.sort(candidates);
  11.     Deque<Integer> path = new ArrayDeque<>(len);
  12.     dfs(candidates, len, 0, target, path, res);
  13.     return res;
  14. }
  16. /**
  17.  * @param candidates 候选数组
  18.  * @param len        冗余变量
  19.  * @param begin      从候选数组的 begin 位置开始搜索
  20.  * @param target     表示剩余，这个值一开始等于 target，基于题目中说明的"所有数字（包括目标数）都是正整数"这个条件
  21.  * @param path       从根结点到叶子结点的路径
  22.  * @param res
  23.  */
  24. private void dfs(int[] candidates, int len, int begin, int target, Deque<Integer> path, List<List<Integer>> res) {
  25.     if (target == 0) {
  26.         res.add(new ArrayList<>(path));
  27.         return;
  28.     }
  29.     for (int i = begin; i < len; i++) {
  30.         // 大剪枝：减去 candidates[i] 小于 0，减去后面的 candidates[i + 1]、
  31.         // candidates[i + 2] 肯定也小于 0，因此用 break
  32.         if (target - candidates[i] < 0) {
  33.             break;
  34.         }
  36.         // 小剪枝：同一层相同数值的结点，从第 2 个开始，候选数更少，结果一定发生重复，
  37.         // 因此跳过，用 continue
  38.         if (i > begin && candidates[i] == candidates[i - 1]) {
  39.             continue;
  40.         }
  42.         path.addLast(candidates[i]);
  43.         // 调试语句 ①
  44.         // System.out.println("递归之前 => " + path + "，剩余 = " + 
  45.         // (target - candidates[i]));
  47.         // 因为元素不可以重复使用，这里递归传递下去的是 i + 1 而不是 i
  48.         dfs(candidates, len, i + 1, target - candidates[i], path, res);
  50.         path.removeLast();
  51.         // 调试语句 ②
  52.         // System.out.println("递归之后 => " + path + "，剩余 = " + 
  53.         // (target - candidates[i]));
  54.     }
  55. }
  57. public static void main(String[] args) {
  58.     int[] candidates = new int[]{10, 1, 2, 7, 6, 1, 5};
  59.     int target = 8;
  60.     Solution solution = new Solution();
  61.     List<List<Integer>> res = solution.combinationSum2(candidates, target);
  62.     System.out.println("输出 => " + res);
  63. }

}

递归之前 => [1]，剩余 = 7 递归之前 => [1, 1]，剩余 = 6 递归之前 => [1, 1, 2]，剩余 = 4 递归之后 => [1, 1]，剩余 = 4 递归之前 => [1, 1, 5]，剩余 = 1 递归之后 => [1, 1]，剩余 = 1 递归之前 => [1, 1, 6]，剩余 = 0 递归之后 => [1, 1]，剩余 = 0 递归之后 => [1]，剩余 = 6 递归之前 => [1, 2]，剩余 = 5 递归之前 => [1, 2, 5]，剩余 = 0 递归之后 => [1, 2]，剩余 = 0 递归之后 => [1]，剩余 = 5 递归之前 => [1, 5]，剩余 = 2 递归之后 => [1]，剩余 = 2 递归之前 => [1, 6]，剩余 = 1 递归之后 => [1]，剩余 = 1 递归之前 => [1, 7]，剩余 = 0 递归之后 => [1]，剩余 = 0 递归之后 => []，剩余 = 7 递归之前 => [2]，剩余 = 6 递归之前 => [2, 5]，剩余 = 1 递归之后 => [2]，剩余 = 1 递归之前 => [2, 6]，剩余 = 0 递归之后 => [2]，剩余 = 0 递归之后 => []，剩余 = 6 递归之前 => [5]，剩余 = 3 递归之后 => []，剩余 = 3 递归之前 => [6]，剩余 = 2 递归之后 => []，剩余 = 2 递归之前 => [7]，剩余 = 1 递归之后 => []，剩余 = 1 输出 => [[1, 1, 6], [1, 2, 5], [1, 7], [2, 6]] ```