leetcode-53：最大子序和

问题

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和

示例 1：
输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6

示例 2：
输入：nums = [1]
输出：1

示例 3：
输入：nums = [0]
输出：0

示例 4：
输入：nums = [-1]
输出：-1

示例 5：
输入：nums = [-100000]
输出：-100000

贪心

最大子序和—贪心

思路

动规五部曲如下：

• 确定dp数组以及下标的含义

  • **dp[i]**：包括下标**i**之前的最大连续子序列和为**dp[i]**

• 确定递推公式

  • dp[i]只有两个方向可以推出来：
    • dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
    • nums[i]，即：从头开始计算当前连续子序列和
  • 一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);

• dp数组如何初始化

  • 从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态，dp[0]就是递推公式的基础
  • 根据dp[i]的定义，很明显dp[0]因为为nums[0]即dp[0] = nums[0]

• 确定遍历顺序

  • 从前向后遍历

• 举例推导dp数组

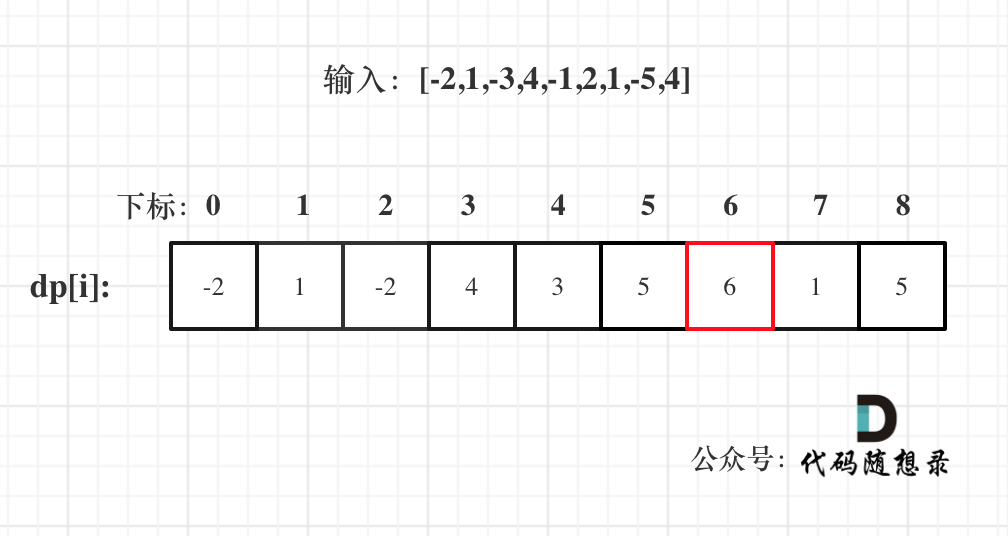
注意最后的结果可不是dp[nums.size() - 1]！ ，而是dp[6]
在回顾一下dp[i]的定义：包括下标i之前的最大连续子序列和为dp[i]
那么我们要找最大的连续子序列，就应该找每一个i为终点的连续最大子序列
所以在递推公式的时候，可以直接选出最大的dp[i]

class Solution {
    public int maxSubArray(int[] nums) {
        if (nums.length == 0) return 0;
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        int result = dp[0];
        for (int i = 1; i < nums.length; i++) {
            dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
            if (dp[i] > result) 
                result = dp[i]; // result 保存dp[i]的最大值
        }
        return result;
    }
}

• 时间复杂度：O(n)
• 空间复杂度：O(n)