问题
给定一个非负整数数组 nums ,你最初位于数组的第一个下标
数组中的每个元素代表你在该位置可以跳跃的最大长度
判断你是否能够到达最后一个下标
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为3的位置。但该下标的最大跳跃长度是0, 所以永远不可能到达最后一个下标
思路
刚看到本题一开始可能想:当前位置元素如果是3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?
其实跳几步无所谓,关键在于可跳的覆盖范围
不一定非要明确一次究竟跳几步,每次取最大的跳跃步数,这个就是可以跳跃的覆盖范围
这个范围内,别管是怎么跳的,反正一定可以跳过来
那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点!
每次移动取最大跳跃步数(得到最大的覆盖范围),每移动一个单位,就更新最大覆盖范围
贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点
局部最优推出全局最优,找不出反例,试试贪心!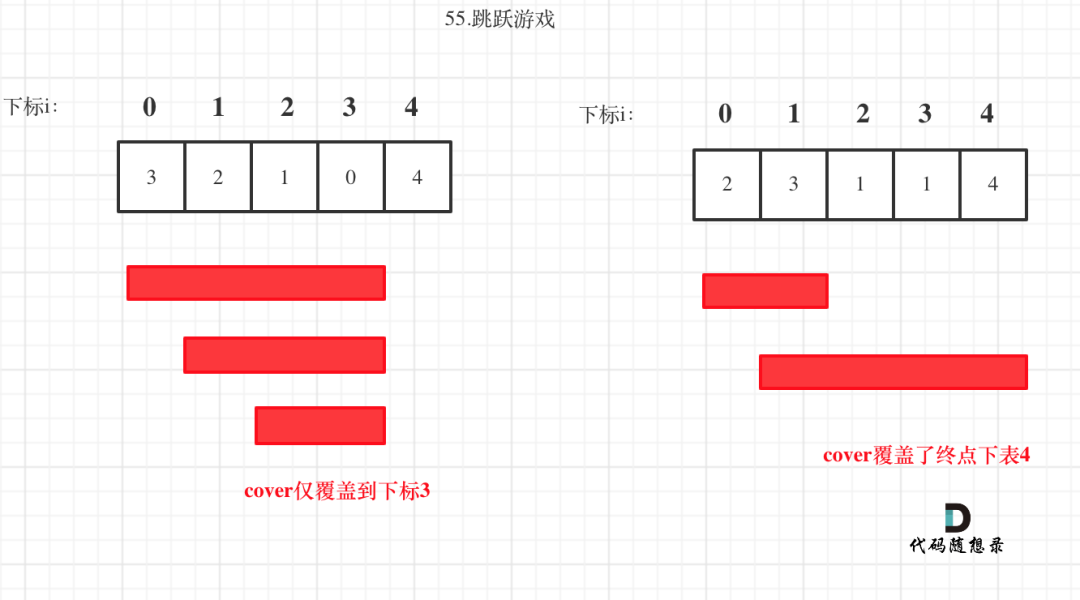
i每次移动只能在cover的范围内移动,每移动一个元素,cover得到该元素数值(新的覆盖范围)的补充,让i继续移动下去
而cover每次只取max(该元素数值补充后的范围, cover本身范围)
如果cover大于等于了终点下标,直接return true就可以了
class Solution {public boolean canJump(int[] nums) {int cover = 0;if (nums.length == 1)return true; // 只有一个元素,就是能达到for (int i = 0; i <= cover; i++) { // 注意这里是小于等于covercover = Math.max(i + nums[i], cover);if (cover >= nums.length - 1)return true; // 说明可以覆盖到终点了}return false;}}
- 时间复杂度:
,其中
n为数组的大小。只需要访问nums数组一遍,共n个位置 - 空间复杂度:
,不需要额外的空间开销

