问题

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1

示例 1：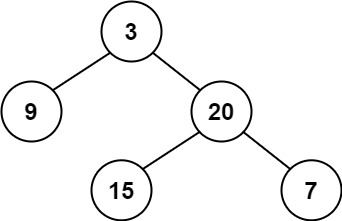
leetcode-110：平衡二叉树 - 图1
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：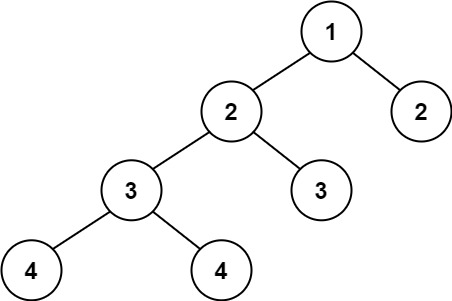
leetcode-110：平衡二叉树 - 图2
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：
输入：root = []
输出：true

分析

这里强调一波概念：

  • 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数
  • 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数

但leetcode中强调的深度和高度很明显是按照节点来计算的，如图：
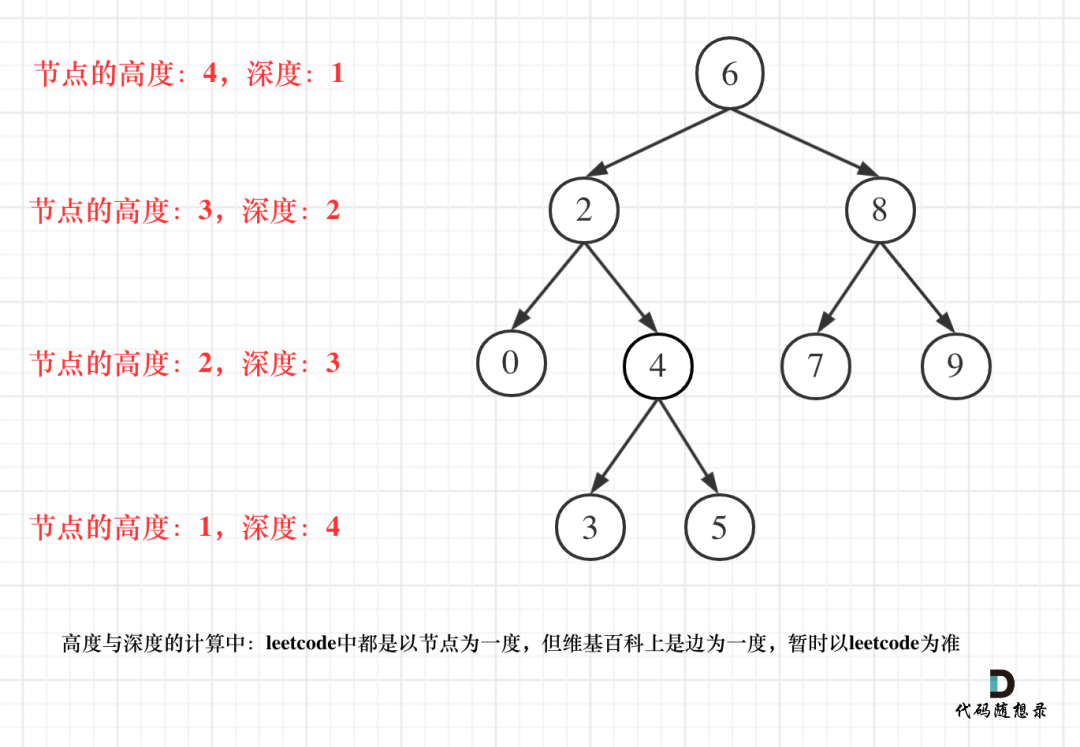
leetcode-110：平衡二叉树 - 图3
关于根节点的深度究竟是1还是0，不同的地方有不一样的标准，leetcode的题目中都是以节点为一度，即根节点深度是1。但维基百科上定义用边为一度，即根节点的深度是0，我们暂时以leetcode为准

因为求深度可以从上到下去查，所以需要前序遍历（中左右），而高度只能从下到上去查，所以只能后序遍历（左右中）

解法：递归

递归三步曲分析：

  • 明确递归函数的参数和返回值 ：参数的话为传入的节点指针，就没有其他参数需要传递了，返回值要返回传入节点为根节点树的深度

    • 那么如何标记左右子树是否差值大于1呢： 如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。 所以如果已经不是二叉平衡树了，可以返回-1 来标记已经不符合平衡树的规则了
      1. // -1 表示已经不是平衡二叉树了，否则返回值是以该节点为根节点树的高度
      2. int getDepth(TreeNode node)

  • 明确终止条件 ：递归的过程中依然是遇到空节点了为终止，返回0，表示当前节点为根节点的高度为0

    1. if (node == null) {
    2.   return 0;
    3. }

  • 明确单层递归的逻辑 ：如何判断当前传入节点为根节点的二叉树是否是平衡二叉树呢，当然是左子树高度和右子树高度相差。 分别求出左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则则返回-1，表示已经不是二叉树了 ```java int leftDepth = depth(node.left); // 左 if (leftDepth == -1) return -1;
    int rightDepth = depth(node.right); // 右 if (rightDepth == -1) return -1;

int result; if (Math.abs(leftDepth - rightDepth) > 1) { // 中 result = -1; } else { result = 1 + max(leftDepth, rightDepth); // 以当前节点为根节点的最大高度 }

return result;

  1. ```java
  2. class Solution {
  3.     public boolean isBalanced(TreeNode root) {
  4.         return getDepth(root) == -1 ? false : true;
  5.     }    
  7.     public int getDepth(TreeNode root){
  8.         if(root == null){
  9.             return 0;
  10.         }
  12.         int leftDepth = getDepth(root.left); // 左
  13.         if (leftDepth == -1) 
  14.             return -1;     
  16.         int rightDepth = getDepth(root.right); // 右
  17.         if (rightDepth == -1) 
  18.             return -1;
  20.         int result;
  21.         if (Math.abs(leftDepth - rightDepth) > 1) {  // 中
  22.             result = -1;
  23.         } else {
  24.             result = 1 + Math.max(leftDepth, rightDepth); // 以当前节点为根节点的最大高度
  25.         }
  27.         return result;
  28.     }
  29. }

官解一：自顶向下递归

具体做法类似于二叉树的前序遍历，即对于当前遍历到的节点，首先计算左右子树的高度，如果左右子树的高度差是否不超过 1，再分别递归地遍历左右子节点，并判断左子树和右子树是否平衡。这是一个自顶向下的递归的过程

class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) {
            return true;
        } else {
            return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
        }
    }

    public int height(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            return Math.max(height(root.left), height(root.right)) + 1;
        }
    }
}
  • 时间复杂度：leetcode-110：平衡二叉树 - 图4，其中 n 是二叉树中的节点个数
  • 空间复杂度：leetcode-110：平衡二叉树 - 图5，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n

官解二：自底向上递归

自顶向下递归，对于同一个节点，函数 height 会被重复调用，导致时间复杂度较高。如果使用自底向上的做法，则对于每个节点，函数 height 只会被调用一次
自底向上递归的做法类似于后序遍历，对于当前遍历到的节点，先递归地判断其左右子树是否平衡，再判断以当前节点为根的子树是否平衡。如果一棵子树是平衡的，则返回其高度（高度一定是非负整数），否则返回 -1。如果存在一棵子树不平衡，则整个二叉树一定不平衡

class Solution {
    public boolean isBalanced(TreeNode root) {
        return height(root) >= 0;
    }

    public int height(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = height(root.left);
        int rightHeight = height(root.right);
        if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) {
            return -1;
        } else {
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }
}
  • 时间复杂度：leetcode-110：平衡二叉树 - 图6，其中 n 是二叉树中的节点个数。使用自底向上的递归，每个节点的计算高度和判断是否平衡都只需要处理一次，最坏情况下需要遍历二叉树中的所有节点，因此时间复杂度是 leetcode-110：平衡二叉树 - 图7
  • 空间复杂度：leetcode-110：平衡二叉树 - 图8，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n