问题

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：
实现 MyQueue 类：

  • void push(int x) 将元素 x 推到队列的末尾
  • int pop() 从队列的开头移除并返回元素
  • int peek() 返回队列开头的元素
  • boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：
你只能使用标准的栈操作 —— 也就是只有 push to top，peek/pop from top，size 和 is empty 操作是合法的
你所使用的语言也许不支持栈。你可以使用 list或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可

进阶：
你能否实现每个操作均摊时间复杂度为 O(1) 的队列？换句话说，执行 n 个操作的总时间复杂度为 O(n) ，即使其中一个操作可能花费较长时间。

示例：

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

思路

队列是一种先进先出（first in - first out， FIFO）的数据结构，队列中的元素都从后端（rear）入队（push），从前端（front）出队（pop）
栈是一种后进先出（last in - first out， LIFO）的数据结构，栈中元素从栈顶（top）压入（push)，也从栈顶弹出（pop）
为了满足队列的 FIFO 的特性，我们需要用到两个栈，用它们其中一个来反转元素的入队顺序，用另一个来存储元素的最终顺序

方法一（入队 - O(n)， 出队 - O(1)）

入队（push）

一个队列是 FIFO 的，但一个栈是 LIFO 的。这就意味着最新压入的元素必须得放在栈底。为了实现这个目的，我们首先需要把 s1 中所有的元素移到 s2 中，接着把新元素压入 s2。最后把s2 中所有的元素弹出，再把弹出的元素压入 s1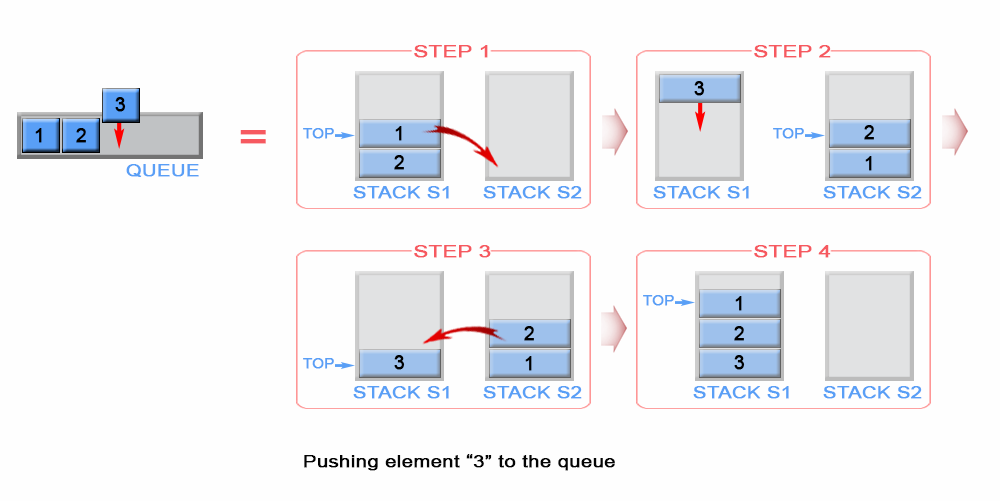
leetcode-232：用栈实现队列 - 图1

empty()和isEmpty()

  • java.util.Stack 继承类 java.util.Vector
  • empty()方法是Stack自己实现的方法
  • isEmpty() 是从Vector继承的方法
  • 其实两者用法差不多一样
  1. private int front;
  3. public void push(int x) {
  4.     if (s1.empty())
  5.         front = x;
  6.     while (!s1.isEmpty())
  7.         s2.push(s1.pop());
  8.     s2.push(x);
  9.     while (!s2.isEmpty())
  10.         s1.push(s2.pop());
  11. }
  • 时间复杂度：leetcode-232：用栈实现队列 - 图2。对于除了新元素之外的所有元素，它们都会被压入两次，弹出两次。新元素只被压入一次，弹出一次。这个过程产生了 4n + 2 次操作，其中 n 是队列的大小。由于压入操作和弹出操作的时间复杂度为leetcode-232：用栈实现队列 - 图3， 所以时间复杂度为leetcode-232：用栈实现队列 - 图4
  • 空间复杂度：leetcode-232：用栈实现队列 - 图5。需要额外的内存来存储队列中的元素

出队（pop）

直接从 s1 弹出就可以了，因为 s1 的栈顶元素就是队列的队首元素。同时我们把弹出之后 s1 的栈顶元素赋值给代表队首元素的 front 变量

  1. // Removes the element from the front of queue.
  2. public void pop() {
  3.     s1.pop();
  4.     if (!s1.empty())
  5.         front = s1.peek();
  6. }
  • 时间复杂度：leetcode-232：用栈实现队列 - 图6
  • 空间复杂度：leetcode-232：用栈实现队列 - 图7
  • 下方函数一样

判断空（empty）

s1 存储了队列所有的元素，所以只需要检查 s1 的是否为空就可以了

  1. public boolean empty(){
  2.     return s1.isEmpty();
  3. }

取队首元素（peek）

算法中，用了 front 变量来存储队首元素，在每次入队操作或者出队操作之后这个变量都会随之更新

  1. public int peek() {
  2.   return front;
  3. }

方法二（入队 - O(1)，出队 - 摊还复杂度 O(1)）

入队（push）

新元素总是压入 s1 的栈顶，同时我们会把 s1 中压入的第一个元素赋值给作为队首元素的 front 变量（front不是模拟的整个队列的队首元素，而是整个队列在s1栈这一段最前面的元素，或者是是s1栈最下面的元素。这样peek的时候，如果s2不为空，那么s2的栈顶元素就是队首元素，否则s1最下面的元素，即front是现在队首的元素）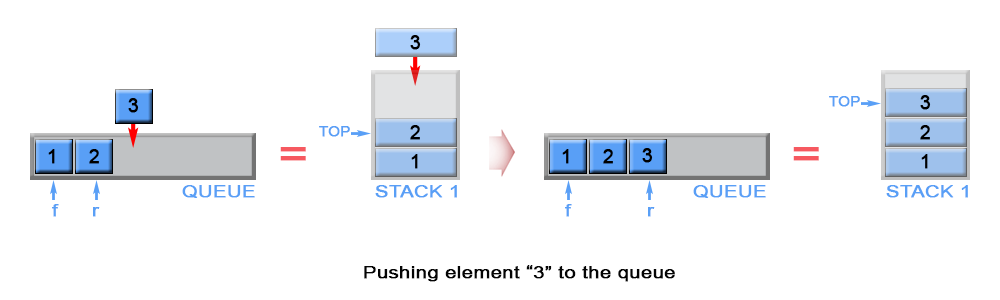
leetcode-232：用栈实现队列 - 图8

  1. private Stack<Integer> s1 = new Stack<>();
  2. private Stack<Integer> s2 = new Stack<>();
  4. // Push element x to the back of queue.
  5. public void push(int x) {
  6.     if (s1.empty())
  7.         front = x;
  8.     s1.push(x);
  9. }
  • 时间复杂度：leetcode-232：用栈实现队列 - 图9。向栈压入元素的时间复杂度为leetcode-232：用栈实现队列 - 图10
  • 空间复杂度：leetcode-232：用栈实现队列 - 图11。需要额外的内存来存储队列元素

出队（pop）

根据栈 LIFO 的特性，s1中第一个压入的元素在栈底。为了弹出s1的栈底元素，我们得把s1中所有的元素全部弹出，再把它们压入到另一个栈s2中，这个操作会让元素的入栈顺序反转过来。通过这样的方式，s1中栈底元素就变成了s2的栈顶元素，这样就可以直接从s2将它弹出了。一旦s2变空了，我们只需把s1中的元素再一次转移到 s2就可以了

  1. // Removes the element from in front of queue.
  2. public void pop() {
  3.     if (s2.isEmpty()) {
  4.         while (!s1.isEmpty())
  5.             s2.push(s1.pop());
  6.     }
  7.     s2.pop();    
  8. }
  • 时间复杂度：leetcode-232：用栈实现队列 - 图12，最坏情况下的时间复杂度leetcode-232：用栈实现队列 - 图13
    • 在最坏情况下，s2 为空，算法需要从 s1 中弹出 n 个元素，然后再把这 n 个元素压入 s2，在这里 n代表队列的大小。这个过程产生了 2n 步操作，时间复杂度为 leetcode-232：用栈实现队列 - 图14。但当 s2 非空时，算法就只有 leetcode-232：用栈实现队列 - 图15 的时间复杂度
    • 直接考虑每个元素即可，无论是哪个元素，都是入栈两次，出栈两次(同理)，所以平均复杂度都是leetcode-232：用栈实现队列 - 图16
  • 空间复杂度 ： leetcode-232：用栈实现队列 - 图17

判断空（empty）

s1和 s2 都存有队列的元素，所以只需要检查 s1 和 s2 是否都为空就可以了

  1. // Return whether the queue is empty.
  2. public boolean empty() {
  3.     return s1.isEmpty() && s2.isEmpty();
  4. }

取队首元素（peek)

我们定义了 front 变量来保存队首元素，每次 入队 操作我们都会随之更新这个变量。当 s2 为空，front变量就是队首元素，当 s2 非空，s2的栈顶元素就是队首元素

  1. // Get the front element.
  2. public int peek() {
  3.     if (!s2.isEmpty()) {
  4.         return s2.peek();
  5.     }
  6.     return front;
  7. }
  • 时间复杂度：leetcode-232：用栈实现队列 - 图18。队首元素要么是之前就被计算出来的，要么就是 s2 栈顶元素
  • 空间复杂度：leetcode-232：用栈实现队列 - 图19

用栈实现队列

自解

法一存在问题，沿用法二的思路

  • 在push数据的时候，只要数据放进输入栈就好
  • 在pop的时候，操作就复杂一些
    • 输出栈如果为空，就把进栈数据全部导入进来（注意是全部导入），再从出栈弹出数据
    • 如果输出栈不为空，则直接从出栈弹出数据就可以了

  • 最后如何判断队列为空呢？如果进栈和出栈都为空的话，说明模拟的队列为空了

    1. class MyQueue {
    3.   private int front;
    4.   Stack<Integer> s1;
    5.   Stack<Integer> s2;
    7.   /** Initialize your data structure here. */
    8.   public MyQueue() {
    9.       s1 = new Stack();
    10.       s2 = new Stack();
    11.   }
    13.   /** Push element x to the back of queue. */
    14.   public void push(int x) {
    15.       if (s1.empty())
    16.           front = x;
    17.       s1.push(x);
    18.   }
    20.   /** Removes the element from in front of queue and returns that element. */
    21.   public int pop() {
    22.       if (s2.isEmpty()) {  // 只有当s2为空的时候，再从s1里导入数据（导入s1全部数据）
    23.           while (!s1.isEmpty())  // 从s1导入数据直到s1为空
    24.               s2.push(s1.pop());
    25.       }
    26.       return s2.pop();    
    27.   }
    29.   /** Get the front element. */
    30.   public int peek() {
    31.       if (!s2.isEmpty()) {
    32.           return s2.peek();
    33.       }
    34.       return front;
    35.   }
    37.   /** Returns whether the queue is empty. */
    38.   public boolean empty() {
    39.       return s1.isEmpty() && s2.isEmpty();
    40.   }
    41. }