字符串 - leetcode-28：实现strStr() - 《算法珠玑》

问题
C++思路讲解
自解

问题

实现 strStr() 函数。给定一个haystack字符串和一个needle字符串，在haystack字符串中找出needle字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1

示例 1:
输入: haystack = “hello”, needle = “ll”
输出: 2

示例 2:
输入: haystack = “aaaaa”, needle = “bba”
输出: -1

说明：当needle是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。对于本题而言，当 needle是空字符串时我们应当返回 0 。这与C语言的strstr()以及Java的indexOf()定义相符

public int indexOf(int ch)：返回指定字符在字符串中第一次出现处的索引，如果此字符串中没有这样的字符，则返回 -1
public int indexOf(int ch, int fromIndex)：返回从fromIndex位置开始查找指定字符在字符串中第一次出现处的索引，如果此字符串中没有这样的字符，则返回 -1
int indexOf(String str)：返回指定字符在字符串中第一次出现处的索引，如果此字符串中没有这样的字符，则返回 -1
int indexOf(String str, int fromIndex)：返回从 fromIndex位置开始查找指定字符在字符串中第一次出现处的索引，如果此字符串中没有这样的字符，则返回 -1

C++思路讲解

构造next数组

我们定义一个函数getNext来构建next数组，函数参数为指向next数组的指针，和一个字符串：

void getNext(int* next, const string& s)

构造next数组其实就是计算模式串s，前缀表的过程。主要有如下三步：

初始化
处理前后缀不相同的情况
处理前后缀相同的情况
初始化：定义两个指针i和j，j指向前缀终止位置（严格来说是终止位置减一的位置），i指向后缀终止位置（与j同理）。然后还要对next数组进行初始化赋值，如下：
```
int j = -1;
next[0] = j;
```
j为什么要初始化为 -1呢，因为之前说过前缀表要统一减一的操作，所以j初始化为-1
next[i]表示i（包括i）之前最长相等的前后缀长度（其实就是j），所以初始化next[0] = j
处理前后缀不相同的情况

因为j初始化为-1，那么i就从1开始，进行s[i]与s[j+1]的比较。则遍历模式串s的循环下标i要从1开始

for(int i = 1; i < s.size(); i++)

如果s[i]与s[j+1]不相同，也就是遇到前后缀末尾不相同的情况，就要向前回溯。怎么回溯呢？
next[j]就是记录着j（包括j）之前的子串的相同前后缀的长度
那么s[i]与s[j+1]不相同，就要找 j+1前一个元素在next数组里的值（就是next[j]）

while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
    j = next[j]; // 向前回溯
}

处理前后缀相同的情况

如果s[i]与s[j + 1]相同，那么就同时向后移动i和j说明找到了相同的前后缀，同时还要将j（前缀
的长度）赋给next[i]，因为next[i]要记录相同前后缀的长度

if (s[i] == s[j + 1]) { // 找到相同的前后缀
    j++;
}
next[i] = j;

最后整体构建next数组的函数代码如下：

void getNext(int* next, const string& s){
    int j = -1;
    next[0] = j;
    for(int i = 1; i < s.size(); i++) { // 注意i从1开始
        while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
            j = next[j]; // 向前回溯
        }
        if (s[i] == s[j + 1]) { // 找到相同的前后缀
            j++;
        }
        next[i] = j; // 将j（前缀的长度）赋给next[i]
    }
}

代码构造next数组的逻辑流程动画如下：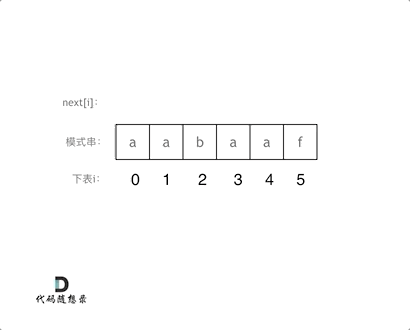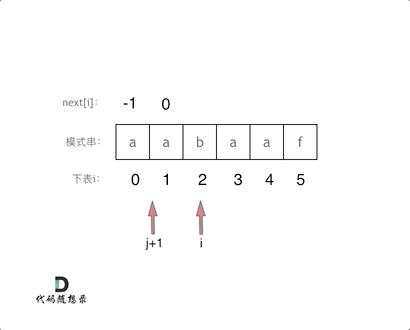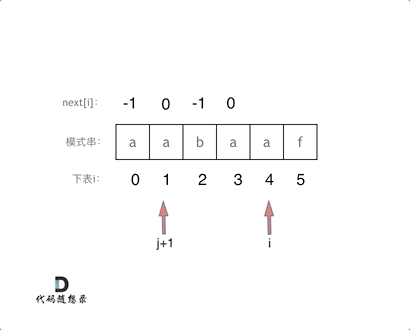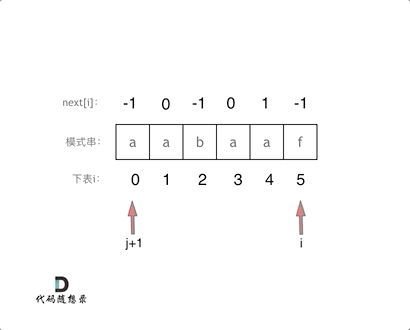
leetcode-28：实现strStr() - 图1
得到了next数组之后，就要用这个来做匹配了

使用next数组来做匹配

在文本串s里找是否出现过模式串t
定义两个下标j指向模式串起始位置，i指向文本串其实位置
j初始值依然为-1，i就从0开始，遍历文本串
```
for (int i = 0; i < s.size(); i++)
```
接下来就是s[i]与t[j + 1]（因为j从-1开始的）进行比较。如果s[i]与t[j + 1]不相同，j就要从next数组里寻找下一个匹配的位置
```
while(j >= 0 && s[i] != t[j + 1]) {
  j = next[j];
}
```
如果s[i]与t[j + 1]相同，那么i和j同时向后移动
```
if (s[i] == t[j + 1]) {
  j++; // i的增加在for循环里
}
```
如何判断在文本串s里出现了模式串t呢，如果j指向了模式串t的末尾，那么就说明模式串t完全匹配文本串s里的某个子串了

本题要在文本串字符串中找出模式串出现的第一个位置 (从0开始)，所以返回当前在文本串匹配模式串的位置i减去模式串的长度，就是文本串字符串中出现模式串的第一个位置

if (j == (t.size() - 1) ) {
    return (i - t.size() + 1);
}

那么使用next数组，用模式串匹配文本串的整体代码如下：

int j = -1; // 因为next数组里记录的起始位置为-1
for (int i = 0; i < s.size(); i++) { // 注意i就从0开始
    while(j >= 0 && s[i] != t[j + 1]) { // 不匹配
        j = next[j]; // j 寻找之前匹配的位置
    }
    if (s[i] == t[j + 1]) { // 匹配，j和i同时向后移动
        j++; // i的增加在for循环里
    }
    if (j == (t.size() - 1) ) { // 文本串s里出现了模式串t
        return (i - t.size() + 1);
    }
}

此时所有逻辑的代码都已经写出来了，本题整体代码如下：

class Solution {
public:
    void getNext(int* next, const string& s) {
        int j = -1;
        next[0] = j;
        for(int i = 1; i < s.size(); i++) { // 注意i从1开始
            while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
                j = next[j]; // 向前回溯
            }
            if (s[i] == s[j + 1]) { // 找到相同的前后缀
                j++;
            }
            next[i] = j; // 将j（前缀的长度）赋给next[i]
        }
    }
    int strStr(string haystack, string needle) {
        if (needle.size() == 0) {
            return 0;
        }
        int next[needle.size()];
        getNext(next, needle);
        int j = -1; // // 因为next数组里记录的起始位置为-1
        for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
            while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
                j = next[j]; // j 寻找之前匹配的位置
            }
            if (haystack[i] == needle[j + 1]) { // 匹配，j和i同时向后移动 
                j++; 
            }
            if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串t
                return (i - needle.size() + 1); 
            }
        }
        return -1;
    }
};

自解

class Solution {
    // KMP 算法
    public int strStr(String haystack, String needle) {
        if (pp.isEmpty()) 
            return 0;

        // 分别读取原串和匹配串的长度
        int n = haystack.length(), m = needle.length();
        // 原串和匹配串前面都加空格，使其下标从 1 开始
        haystack = " " + haystack;
        needle = " " + needle;

        char[] s = haystack.toCharArray();
        char[] p = needle.toCharArray();

        // 构建 next 数组，数组长度为匹配串的长度（next 数组是和匹配串相关的）
        int[] next = new int[m + 1];
        // 构造过程 i = 2，j = 0 开始，i 小于等于匹配串长度 【构造 i 从 2 开始】
        for (int i = 2, j = 0; i <= m; i++) {
            // 匹配不成功的话，j = next(j)
            while (j > 0 && p[i] != p[j + 1]) 
                j = next[j];
            // 匹配成功的话，先让 j++
            if (p[i] == p[j + 1]) 
                j++;
            // 更新 next[i]，结束本次循环，i++
            next[i] = j;
        }

        // 匹配过程，i = 1，j = 0 开始，i 小于等于原串长度 【匹配 i 从 1 开始】
        for (int i = 1, j = 0; i <= n; i++) {
            // 匹配不成功 j = next(j)
            while (j > 0 && s[i] != p[j + 1]) 
                j = next[j];
            // 匹配成功的话，先让 j++，结束本次循环后 i++
            if (s[i] == p[j + 1]) 
                j++;
            // 整一段匹配成功，直接返回下标
            if (j == m) 
                return i - m;
        }

        return -1;
    }
}