leetcode-559：N叉树的最大深度

问题

给定一个 N 叉树，找到其最大深度
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数
N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）

示例 1：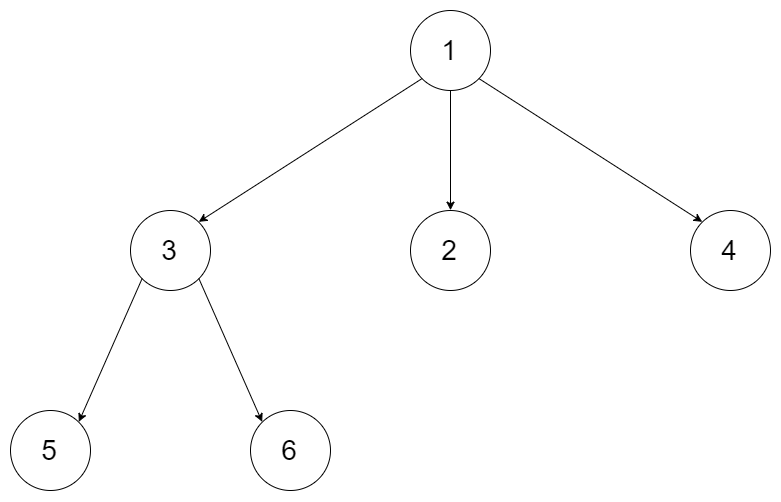

输入：root = [1,null,3,2,4,null,5,6]
输出：3

示例 2：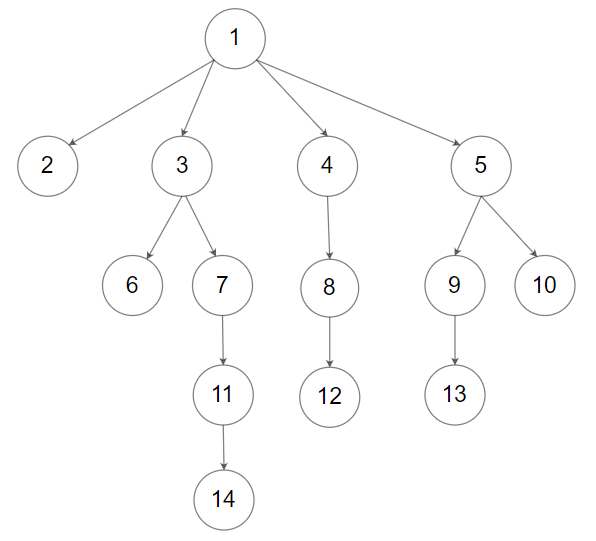

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：5

树节点的定义

// 节点定义
class Node {
  public int val;
  public List<Node> children;
  public Node() {}
  public Node(int _val, List<Node> _children) {
    val = _val;
    children = _children;
  }
}

解法一：递归

写递归最基本的步骤：
1.分析递归能否在原方法上进行，如果不能在原方法上递归，那么需要新建一个递归方法
如何分析呢？看题目要求的返回值与每一层递归返回的值是否相同；
以本题为例，题目要求返回根节点的最大深度；我们要求根节点的最大深度，那么需要获得每一层节点的最大深度，层层累加得来；在本题，题目要求返回的值与每一层递归返回的值完全相同，都是当前节点的最大深度；
因此本题，可以直接在原方法上递归。

2.寻找递归的终点（出口）
如何寻找递归终点（出口）？所以树结构的递归终点是空节点或最底层的叶节点；
因为根节点有可能是null，所以我们先把null的情况判断出来，空节点的深度为0，直接返回0；
接下来是叶节点，如何识别叶节点？没有任何子节点的就是叶节点。叶节点的最大深度是1，因此返回1；
至此，递归的终点写好了

3.思考如何进入下一层递归，以及如何利用递归得到的值
如何进入下一层递归？在递归过程中，传入下一层的相同类型的节点即可；
树的递归，进行下一层递归的是子节点，所以调用方法自身，传入子节点；
本题的子节点放在一个List中，所以遍历List，将每一个子节点进行下一层递归；
下一层递归获得的值就是该子节点的最大深度，需要从这一众子节点的最大深度值中找到最大的；

4.思考如何返回值
方法的返回值，一定要符合每一层递归返回值的共同要求；
在本题中，要返回当前节点的最大深度值；
当前节点的最大深度值 = 所有子节点的最大深度值的最大值 + 1；
题目要求的返回值，是根节点的最大深度值，符合相同的要求，直接返回就好啦！

class Solution{
    public int maxDepth(Node root){
        if(root == null){
            return 0;
        }
        int max = 0;
        for(Node node : root.children){
            max = Math.max(maxDepth(node), max);
        }
        return max + 1;
    }
}

class Solution {
  public int maxDepth(Node root) {
    if (root == null) {
      return 0;
    } else if (root.children.isEmpty()) {
      return 1;  
    } else {
      List<Integer> heights = new LinkedList<>();
      for (Node item : root.children) {
        heights.add(maxDepth(item)); 
      }
      //Collections 类的 max() 方法是用于根据给定集合的元素的自然顺序获取最大元素
      return Collections.max(heights) + 1;
    }
  }
}

• 时间复杂度：每个节点遍历一次，所以时间复杂度是 ，其中 N 为节点数
• 空间复杂度：最坏情况下, 树完全非平衡，
  • 例如，每个节点有且仅有一个孩子节点，递归调用会发生 N 次（等于树的深度），所以存储调用栈需要
  • 但是在最好情况下（树完全平衡），树的高度为。所以在此情况下空间复杂度为

解法二：广度优先遍历（官解）

class Solution{ 
    public int maxDepth(Node root) {
        if (root == null) {
            return 0;
        }
         Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        int level = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                Node cur = queue.poll();
                if (cur != null) {
                    for (Node child : cur.children) {
                        if (child != null) {
                            queue.offer(child);
                        }
                    }
                }
            }
            level++;
        }
        return level;
    }
}

自解

class Solution {
    public int maxDepth(Node root) {
        if (root == null) {
            return 0;
        }
         Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        int level = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            for(int i = 0; i < size; i++){
                Node node = queue.poll();
                queue.addAll(node.children);
            }
            level++;
        }
        return level;
    }
}