leetcode-94：二叉树的中序遍历

思路

为了解释清楚，我说明一下在前序遍历迭代的过程中，其实我们有两个操作：

• 处理：将元素放进数组中
• 访问：遍历节点

分析一下为什么刚刚写的前序遍历的代码，不能和中序遍历通用呢，因为前序遍历的顺序是中左右，先访问的元素是中间节点，要处理的元素也是中间节点，所以刚刚才能写出相对简洁的代码，因为要访问的元素和要处理的元素顺序是一致的，都是中间节点。

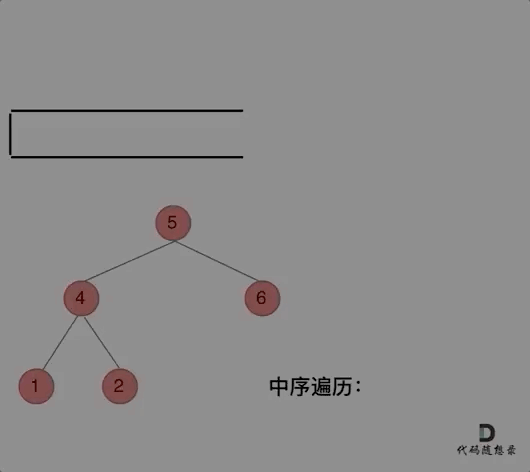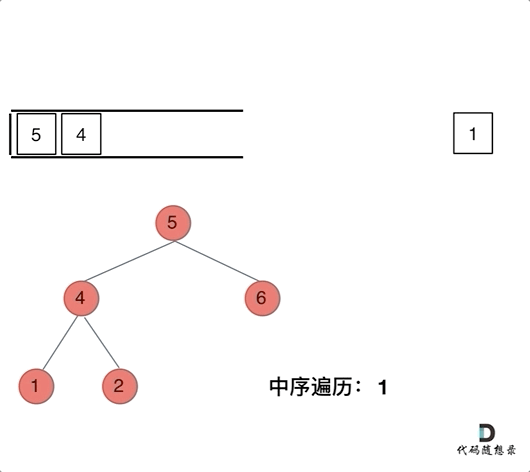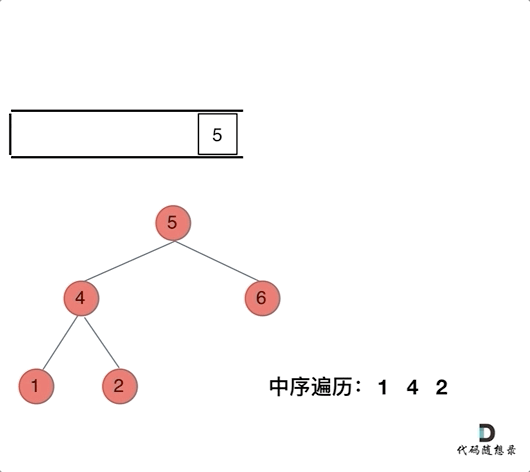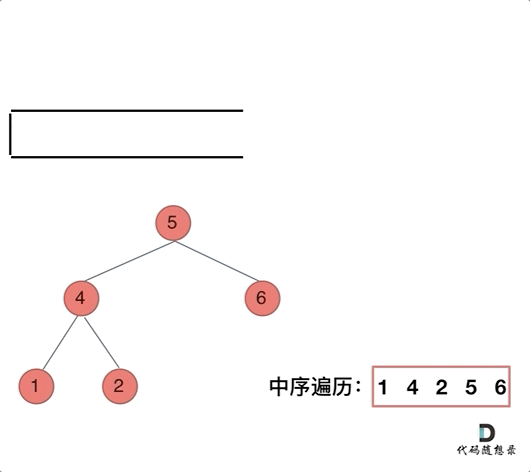
那么再看看中序遍历，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进res数组中），这就造成了处理顺序和访问顺序是不一致的

解法

public class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        // 栈 先进后出
        List<Integer> res = new ArrayList<Integer>();
        Stack<TreeNode> stack = new Stack<>();
        // root为空且stack为空，遍历结束
        while (root != null || !stack.isEmpty()) {
            // 先根后左入栈
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            // 此时root==null，说明上一步的root没有左子树
            // 1. 执行左出栈。因为此时root==null，导致root.right一定为null
            // 2. 执行下一次外层while代码块，根出栈。此时root.right可能存在
            // 3a. 若root.right存在，右入栈，再出栈
            // 3b. 若root.right不存在，重复步骤2
            root = stack.pop();
            res.add(root.val);
            root = root.right;
        }
        return res;
    }
}

时间复杂度：，其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次
空间复杂度：，空间复杂度取决于栈深度，而栈深度在二叉树为一条链的情况下会达到 的级别