leetcode-376：摆动序列

问题

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列

例如， [1, 7, 4, 9, 2, 5]是一个摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的
相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零
子序列可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序

给你一个整数数组 nums，返回 nums 中作为摆动序列的最长子序列的长度

示例 1：
输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3)

示例 2：
输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8)

示例 3：
输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2

思路

本题要求通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序

这要求最大摆动序列又可以修改数组，这得如何修改呢？

来分析一下，要求删除元素使其达到最大摆动序列，应该删除什么元素呢？

用示例二来举例，如图所示：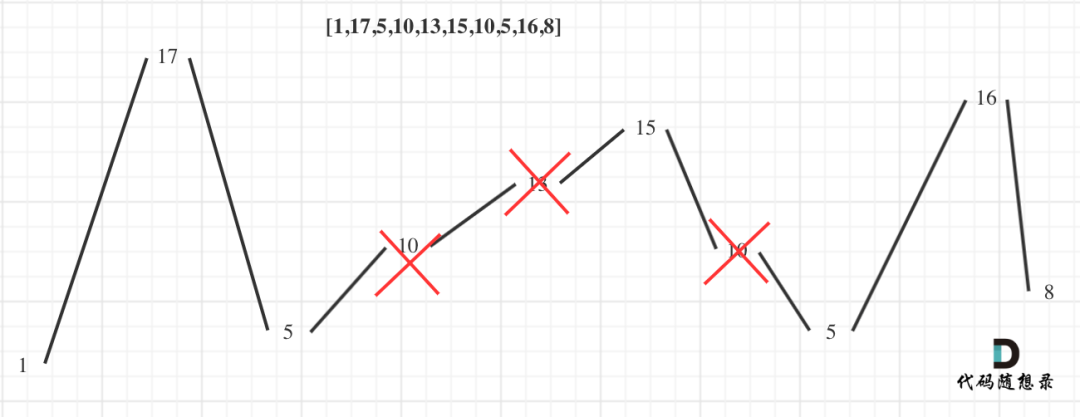

• 局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值
• 整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列

局部最优推出全局最优，并举不出反例，那么试试贪心（为方便表述，以下说的峰值都是指局部峰值）

实际操作上，其实连删除的操作都不用做，因为题目要求的是最长摆动子序列的长度，所以只需要统计数组的峰值数量就可以了（相当于是删除单一坡度上的节点，然后统计长度）
这就是贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点

本题代码实现中，还有一些技巧，例如统计峰值的时候，数组最左面和最右面是最不好统计的
例如序列[2,5]，它的峰值数量是2，如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。所以可以针对序列[2,5]，可以假设为[2,2,5]，这样它就有坡度了即preDiff = 0，如图：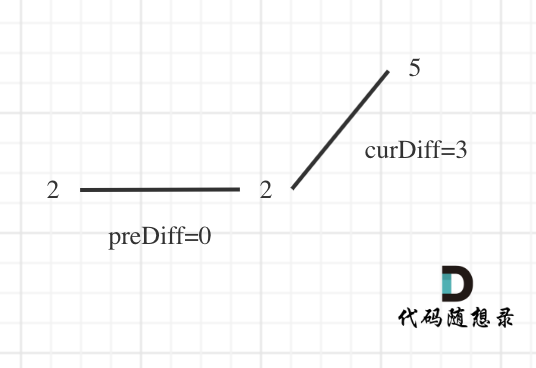

针对以上情形，result初始为1（默认最右面有一个峰值），此时curDiff > 0 && preDiff <= 0，那么result++（计算了左面的峰值），最后得到的result就是2（峰值个数为2即摆动序列长度为2）

class Solution{
    public int wiggleMaxLength(int[] nums){
        if(nums.length <= 1){
            return nums.length;
        }
        int curDiff = 0; //当前的一对差值
        int preDiff = 0; //前一对差值
        int result = 1; //默认序列最右边有一个峰值
        for(int i = 1; i < nums.length; i++){
            curDiff = nums[i] - nums[i - 1];
            //只有preDiff可以等于0
            if((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)){
                result++;
                preDiff = curDiff;
            }
        }
        return result;
    }
}

• 时间复杂度
• 空间复杂度

总结

贪心的题目说简单有的时候就是常识，说难就难在都不知道该怎么用贪心
而这道题目有什么技巧说一下子能想到贪心么？
其实也没有，类似的题目做过了就会想到
此时大家就应该了解了：保持区间波动，只需要把单调区间上的元素移除就可以了