问题

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的

示例 1：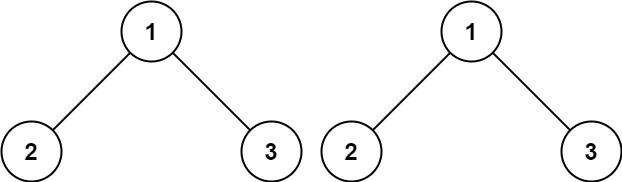
leetcode-100：求相同的树 - 图1
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：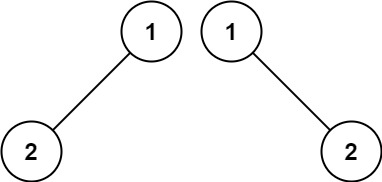
leetcode-100：求相同的树 - 图2
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：
leetcode-100：求相同的树 - 图3
输入：p = [1,2,1], q = [1,1,2]
输出：false

解法一：递归

  1. class Solution {
  2.     public boolean isSameTree(TreeNode p, TreeNode q) {
  3.         if (p == null && q == null) {
  4.             return true;
  5.         } else if (p == null || q == null) {
  6.             return false;
  7.         } else if (p.val != q.val) {
  8.             return false;
  9.         } else {
  10.             return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
  11.         }
  12.     }
  13. }
  • 时间复杂度：leetcode-100：求相同的树 - 图4，其中 m 和 n 分别是两个二叉树的节点数。对两个二叉树同时进行深度优先搜索，只有当两个二叉树中的对应节点都不为空时才会访问到该节点，因此被访问到的节点数不会超过较小的二叉树的节点数
  • 空间复杂度：leetcode-100：求相同的树 - 图5，其中 m 和 n 分别是两个二叉树的节点数。空间复杂度取决于递归调用的层数，递归调用的层数不会超过较小的二叉树的最大高度，最坏情况下，二叉树的高度等于节点数

解法二：广度优先搜索

首先判断两个二叉树是否为空，如果两个二叉树都不为空，则从两个二叉树的根节点开始广度优先搜索

  • 使用两个队列分别存储两个二叉树的节点。初始时将两个二叉树的根节点分别加入两个队列。每次从两个队列各取出一个节点，进行如下比较操作
  • 比较两个节点的值，如果两个节点的值不相同则两个二叉树一定不同；
  • 如果两个节点的值相同，则判断两个节点的子节点是否为空，如果只有一个节点的左子节点为空，或者只有一个节点的右子节点为空，则两个二叉树的结构不同，因此两个二叉树一定不同；
  • 如果两个节点的子节点的结构相同，则将两个节点的非空子节点分别加入两个队列，子节点加入队列时需要注意顺序，如果左右子节点都不为空，则先加入左子节点，后加入右子节点。

如果搜索结束时两个队列同时为空，则两个二叉树相同。如果只有一个队列为空，则两个二叉树的结构不同，因此两个二叉树不同

  1. class Solution {
  2.     public boolean isSameTree(TreeNode p, TreeNode q) {
  3.         if (p == null && q == null) {
  4.             return true;
  5.         } else if (p == null || q == null) {
  6.             return false;
  7.         }
  8.         Queue<TreeNode> queue1 = new LinkedList<TreeNode>();
  9.         Queue<TreeNode> queue2 = new LinkedList<TreeNode>();
  10.         queue1.offer(p);
  11.         queue2.offer(q);
  12.         while (!queue1.isEmpty() && !queue2.isEmpty()) {
  13.             TreeNode node1 = queue1.poll();
  14.             TreeNode node2 = queue2.poll();
  15.             if (node1.val != node2.val) {
  16.                 return false;
  17.             }
  19.             if (node1.left == null ^ node2.left == null) {
  20.                 return false;
  21.             }
  22.             if (node1.right == null ^ node2.right == null) {
  23.                 return false;
  24.             }
  25.             if (node1.left != null) {
  26.                 queue1.offer(node1.left);
  27.             }
  28.             if (node1.right != null) {
  29.                 queue1.offer(node1.right);
  30.             }
  31.             if (node2.left != null) {
  32.                 queue2.offer(node2.left);
  33.             }
  34.             if (node2.right != null) {
  35.                 queue2.offer(node2.right);
  36.             }
  37.         }
  38.         return queue1.isEmpty() && queue2.isEmpty();
  39.     }
  40. }