问题

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案

示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:
输入: nums = [1], k = 1
输出: [1]

思路

这道题目主要涉及到如下三块内容：

  • 要统计元素出现频率
  • 对频率排序

  • 找出前K个高频元素

  • 首先统计元素出现的频率，这一类的问题可以使用map来进行统计

然后是对频率进行排序，这里我们可以使用一种 容器适配器就是优先级队列，也就是一个披着队列外衣的堆，因为优先级队列对外接口只是从队头取元素，从队尾添加元素，再无其他取元素的方式，看起来就是一个队列

  • 而且优先级队列内部元素是自动依照元素的权值排列。那么它是如何有序排列的呢？

缺省情况下优先级队列利用max-heap（大顶堆）完成对元素的排序，这个大顶堆是以vector为表现形式的complete binary tree（完全二叉树）

  • 什么是堆呢？

堆是一颗完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆

所以大家经常说的大顶堆（堆头是最大元素），小顶堆（堆头是最小元素），如果懒得自己实现的话，就直接用priority_queue（优先级队列）就可以了，底层实现都是一样的，从小到大排就是小顶堆，从大到小排就是大顶堆

本题我们就要使用优先级队列来对部分频率进行排序

此时要思考一下，是使用小顶堆呢，还是大顶堆？
题目要求前 K 个高频元素，那么果断用大顶堆啊
那么问题来了，定义一个大小为 k 的大顶堆，在每次移动更新大顶堆的时候，每次弹出都把最大的元素弹出去了，那么怎么保留下来前 K 个高频元素呢
所以我们要用小顶堆，因为要统计最大前k个元素，只有小顶堆每次将最小的元素弹出，最后小顶堆里积累的才是前k个最大元素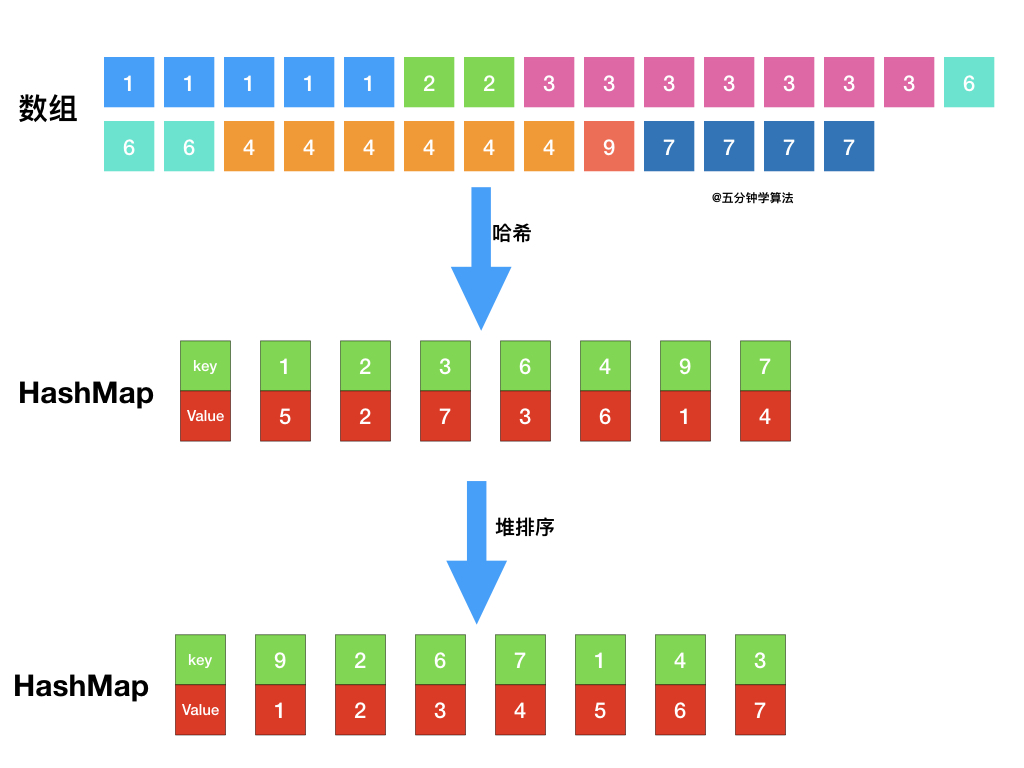
leetcode-347：前k个高频元素 - 图1

具体操作为：

  • 借助 哈希表 来建立数字和其出现次数的映射，遍历一遍数组统计元素的频率
  • 维护一个元素数目为 k 的最小堆
  • 每次都将新的元素与堆顶元素（堆中频率最小的元素）进行比较
  • 如果新的元素的频率比堆顶端的元素大，则弹出堆顶端的元素，将新的元素添加进堆中
  • 最终，堆中的 k 个元素即为前 k 个高频元素

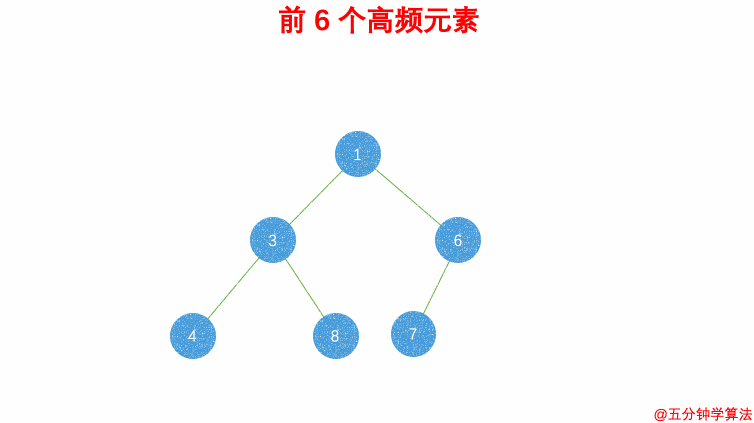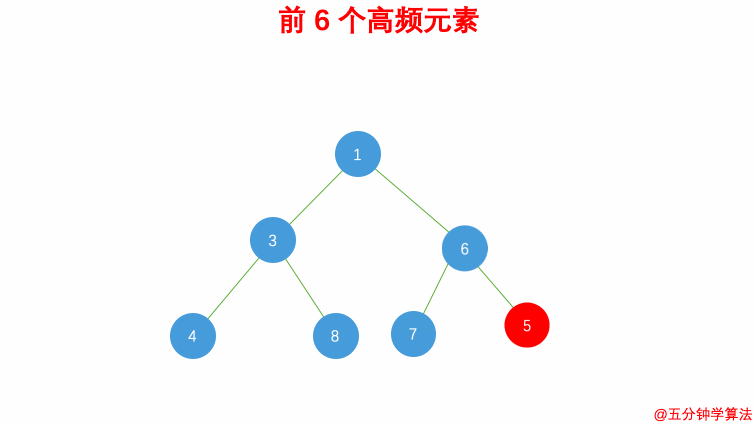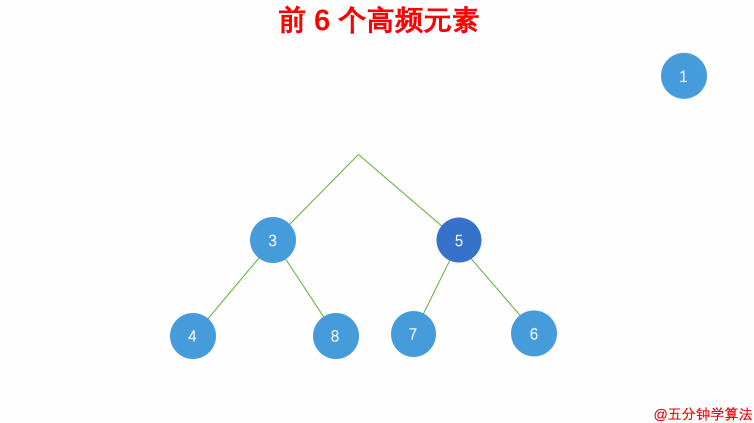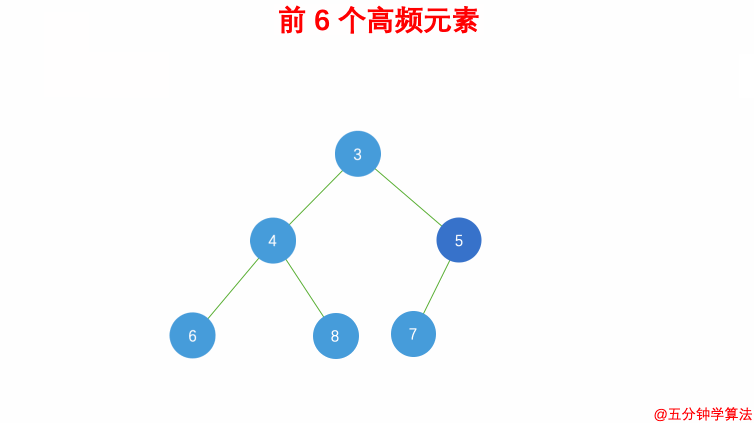
leetcode-347：前k个高频元素 - 图2

解法

  1. class Solution {
  2.     public List<Integer> topKFrequent(int[] nums, int k) {
  3.         // 使用字典，统计每个元素出现的次数，元素为键，元素出现的次数为值
  4.         HashMap<Integer,Integer> map = new HashMap();
  5.         for(int num : nums){
  6.             if (map.containsKey(num)) {
  7.                 // Map.put()方法将获取 Map 集合的所有键名，并存放在一个 Set 集合对象中
  8.                 // Map.get() 方法返回指定键所映射的值
  9.                map.put(num, map.get(num) + 1);
  10.              } else {
  11.                 map.put(num, 1);
  12.              }
  13.         }
  14.         // 遍历map，用最小堆保存频率最大的k个元素
  15.         PriorityQueue<Integer> pq = new PriorityQueue<>(new Comparator<Integer>() {
  16.             public int compare(Integer a, Integer b) {
  17.                 return map.get(a) - map.get(b);
  18.             }
  19.         });
  20.         for (Integer key : map.keySet()) {
  21.             if (pq.size() < k) {
  22.                 pq.add(key);
  23.             } else if (map.get(key) > map.get(pq.peek())) {
  24.                 pq.remove();
  25.                 pq.add(key);
  26.             }
  27.         }
  28.         // 取出最小堆中的元素
  29.         List<Integer> res = new ArrayList<>();
  30.         while (!pq.isEmpty()) {
  31.             res.add(pq.remove());
  32.         }
  33.         Collections.reverse(res); 
  34.         //题目中方法定义的是返回int[]数组，而开头写的方法用的是List,以及res定义的也是              List，所以把方法和res类型改成int,结果遍历一遍就行
  35.         int[] array = res.stream().mapToInt(Integer::valueOf).toArray();
  36.         return array;
  37.     }
  38. }
  • 时间复杂度：leetcode-347：前k个高频元素 - 图3，n 表示数组的长度。首先，遍历一遍数组统计元素的频率，这一系列操作的时间复杂度是 leetcode-347：前k个高频元素 - 图4；接着，遍历用于存储元素频率的 map，如果元素的频率大于最小堆中顶部的元素，则将顶部的元素删除并将该元素加入堆中，这里维护堆的数目是 k
  • 空间复杂度：leetcode-347：前k个高频元素 - 图5，最坏情况下（每个元素都不同），map 需要存储 n 个键值对，优先队列需要存储 k 个元素