二叉搜索树的修改与构造 - leetcode-108：将有序数组转换为二叉搜索树 - 《算法珠玑》

问题
思路
解法一：递归

问题

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵高度平衡二叉搜索树
高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树

示例 1：
leetcode-108：将有序数组转换为二叉搜索树 - 图1
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案

示例 2：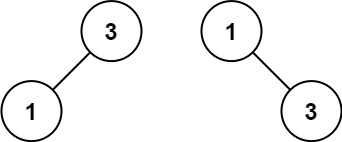
leetcode-108：将有序数组转换为二叉搜索树 - 图3
输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树

思路

本质就是寻找分割点，分割点作为当前节点，然后递归左区间和右区间
分割点就是数组中间位置的节点
那么为问题来了，如果数组长度为偶数，中间节点有两个，取哪一个？
取哪一个都可以，只不过构成了不同的平衡二叉搜索树

解法一：递归

递归三部曲：

确定递归函数返回值及其参数
- 删除二叉树节点，增加二叉树节点，都是用递归函数的返回值来完成，这样是比较方便的；那么本题要构造二叉树，依然用递归函数的返回值来构造中节点的左右孩子
- 再来看参数，首先是传入数组，然后就是left和right，在构造二叉树的时候尽量不要重新定义左右区间数组，而是用下标来操作原数组
```
// 左闭右闭区间[left, right]
TreeNode traversal(int[] nums, int left, int right)
```
确定递归终止条件
- 这里定义的是左闭右闭的区间，所以当区间 left > right的时候，就是空节点了
```
if (left > right) return null;
```

确定单层递归的逻辑

首先取数组中间元素的位置，不难写出int mid = (left + right) / 2，这么写其实有一个问题，就是数值越界，例如left和right都是最大int，这么操作就越界了，在二分法中尤其需要注意！
所以可以这么写：int mid = left + ((right - left) / 2);
取了中间位置，就开始以中间位置的元素构造节点
```
TreeNode root = new TreeNode(nums[mid]);。
```

接着划分区间，root的左孩子接住下一层左区间的构造节点，右孩子接住下一层右区间构造的节点，最后返回root节点，单层递归整体代码如下：

int mid = left + ((right - left) / 2); 
TreeNode root = new TreeNode(nums[mid]);
root.left = traversal(nums, left, mid - 1);
root.right = traversal(nums, mid + 1, right);
return root;

这里int mid = left + ((right - left) / 2);的写法相当于是如果数组长度为偶数，中间位置有两个元素，取靠左边的

class Solution {
public TreeNode traversal(int[] nums, int left, int right) {
   if (left > right) 
       return null;
   int mid = left + ((right - left) / 2); 
   TreeNode root = new TreeNode(nums[mid]);
   root.left = traversal(nums, left, mid - 1);
   root.right = traversal(nums, mid + 1, right);
   return root;
}
public TreeNode sortedArrayToBST(int[] nums) {
   TreeNode root = traversal(nums, 0, nums.length - 1);
   return root;
}
}