leetcode-142：环形链表Ⅱ

问题

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null

为了表示给定链表中的环，我们使用整数 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中

不允许修改给定的链表

进阶：你是否可以使用 空间解决此题？

示例1：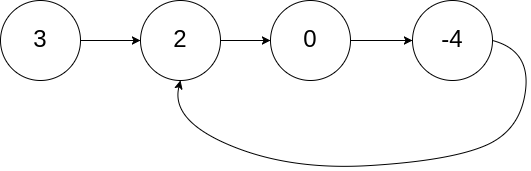

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点

示例2：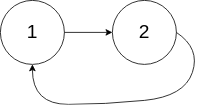

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点

思路

此处需要注意两点：

• 判断链表是否环
• 如果有环，如何找到这个环的入口

判断链表是否有环

快慢指针法：分别定义和指针，从头结点出发，指针每次移动两个节点，指针每次移动一个节点，如果和指针在途中相遇 ，说明这个链表有环

为什么走两个节点，走一个节点，有环的话，一定会在环内相遇呢，而不是永远的错开呢？

• 指针一定先进入环中，如果指针和指针相遇的话，一定是在环中相遇，这是毋庸置疑的

如果有环，如何找到这个环的入口

假设从头结点到环形入口节点 的节点数为，环形入口节点到指针与指针相遇节点节点数为，从相遇节点再到环形入口节点节点数为，如图所示：

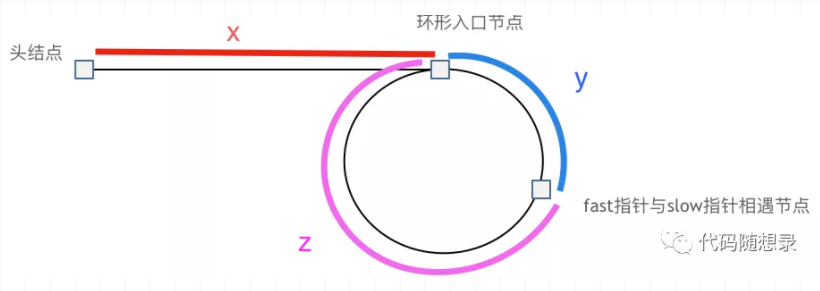
那么相遇时：指针走过的节点数为:，指针走过的节点数：，为指针在环内走了圈才遇到指针，为一圈内节点的个数。因为指针是一步走两个节点，指针一步走一个节点， 所以指针走过的节点数 = 指针走过的节点数 * 2：，即

因为要找环形的入口，那么要求的是，因为表示头结点到环形入口节点的的距离。所以要求，将单独放在左面：，再从中提出一个来，整理之后如下：， 注意这里n一定是大于等于1的，因为指针至少要多走一圈才能相遇指针

这个公式说明什么呢？

• 时，意味着指针在环形里转了一圈之后，就遇到了指针了。当时，公式就化解为，这就意味着，从头结点出发一个指针，从相遇节点也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点，也就是在相遇节点处，定义一个指针，在头结点处定一个指针，让和同时移动，每次移动一个节点， 那么他们相遇的地方就是环形入口的节点
• 时，指针在环形转圈之后才遇到指针，其实这种情况和的时效果是一样的，一样可以通过这个方法找到环形的入口节点，只不过，指针在环里多转了圈，然后再遇到，相遇点依然是环形的入口节点

超时了，为什么啊？？？

package leetcode;
public class leetcode_142 {
    public ListNode detectCycle(ListNode head){
        ListNode fast = head, slow = head;
        while(fast != null && fast.next != null){
            slow = slow.next;
            fast = fast.next.next;
        }
        if (fast == slow){
            ListNode index1 = fast;
            ListNode index2 = head;
            while(index1 != index2){
                index1 = index1.next;
                index2 = index2.next;
            }
            return index2;
        }
        return null;
    }
}

官方题解

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null) {
            return null;
        }
        ListNode slow = head, fast = head;
        while (fast != null) {
            slow = slow.next;
            if (fast.next != null) {
                fast = fast.next.next;
            } else {
                return null;
            }
            if (fast == slow) {
                ListNode ptr = head;
                while (ptr != slow) {
                    ptr = ptr.next;
                    slow = slow.next;
                }
                return ptr;
            }
        }
        return null;
    }
}