问题
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位
返回滑动窗口中的最大值
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
———————————- ———-
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1
输出:[1]
示例 3:
输入:nums = [1,-1], k = 1
输出:[1,-1]
示例 4:
输入:nums = [9,11], k = 2
输出:[11]
示例 5:
输入:nums = [4,-2], k = 2
输出:[4]
思路
对于每个滑动窗口,我们可以使用 的时间遍历其中的每一个元素,找出其中的最大值。对于长度为
n 的数组 nums 而言,窗口的数量为 n-k+1,因此该算法的时间复杂度为,会超出时间限制,因此我们需要进行一些优化
我们可以想到,对于两个相邻(只差了一个位置)的滑动窗口,它们共用着 k-1 个元素,而只有 1 个元素是变化的。我们可以根据这个特点进行优化
方法一:优先队列
对于最大值,可以想到一种非常合适的数据结构,那就是优先队列(堆),其中的大根堆可以帮助我们实时维护一系列元素中的最大值
对于本题而言,初始时,我们将数组 nums 的前 k 个元素放入优先队列中。每当我们向右移动窗口时,我们就可以把一个新的元素放入优先队列中,此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值可能并不在滑动窗口中,在这种情况下,这个值在数组 nums 中的位置出现在滑动窗口左边界的左侧。因此,当我们后续继续向右移动窗口时,这个值就永远不可能出现在滑动窗口中了,我们可以将其永久地从优先队列中移除
我们不断地移除堆顶的元素,直到其确实出现在滑动窗口中。此时,堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系,我们可以在优先队列中存储二元组 (num,index),表示元素 num 在数组中的下标为 index
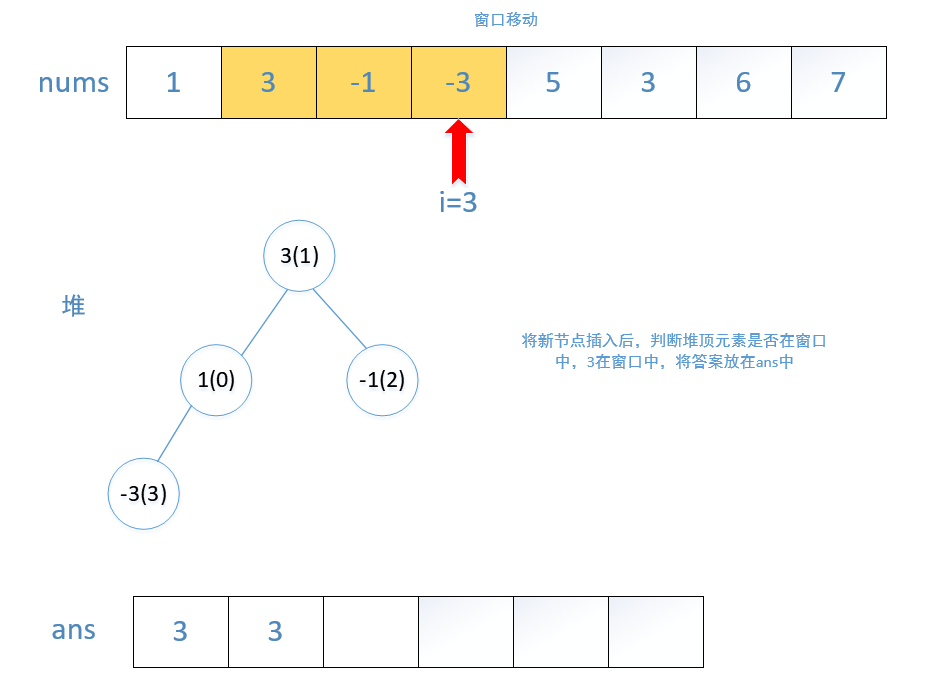
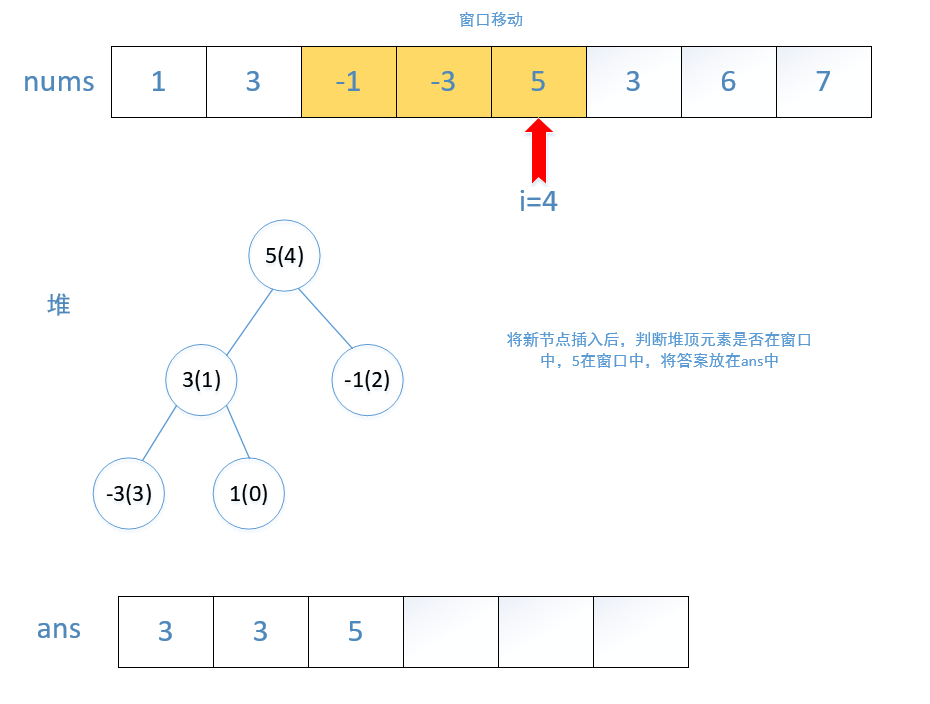


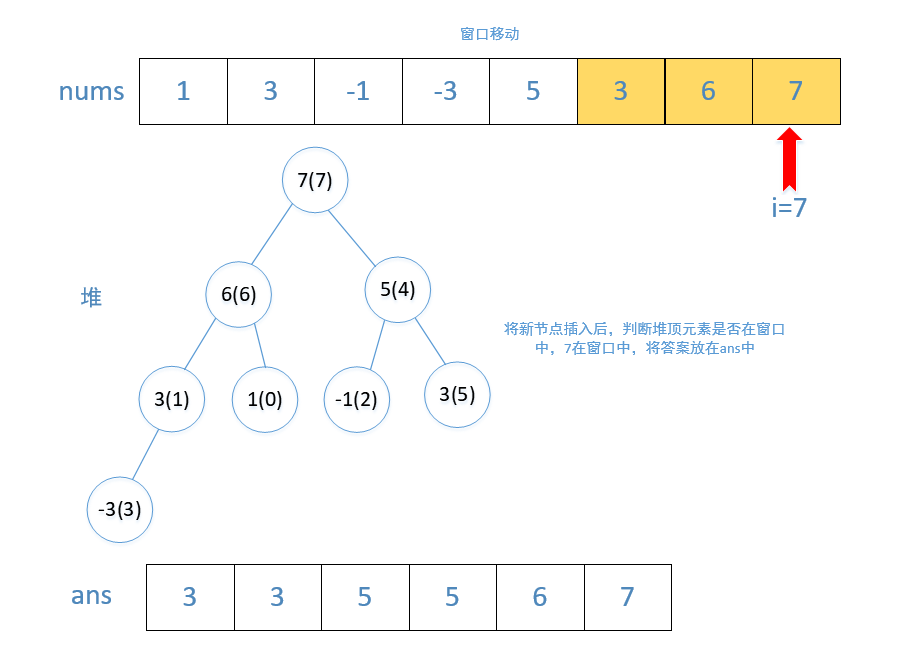
在Java中的优先队列(PriorityQueue)就是堆的数据结构
class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int n = nums.length;// 1. 优先队列存放的是二元组(num,index) : 大顶堆(元素大小不同按元素大小排列,元素大小相同按下标进行排列)// num : 是为了比较元素大小// index : 是为了判断窗口的大小是否超出范围// 当两者的值相同时,比较下标的位置,下标大的在前面PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>(){public int compare(int[] pair1,int[] pair2){return pair1[0] != pair2[0] ? pair2[0] - pair1[0]:pair2[1] - pair1[1];}});// 2. 优先队列初始化 : k个元素的堆for(int i = 0; i < k; i++){pq.offer(new int[]{nums[i],i});}// 3. 处理堆逻辑int[] res = new int[n - k + 1]; // 初始化结果数组长度 :一共有 n - k + 1个窗口res[0] = pq.peek()[0]; // 初始化res[0] : 拿出目前堆顶的元素for(int i = k;i < n;i++){ // 向右移动滑动窗口pq.offer(new int[]{nums[i],i}); // 加入大顶堆中while(pq.peek()[1] <= i - k){ // 循环判断当前队首是否在窗口中,窗口的左边界为i-kpq.poll(); // 维护:堆的大小就是滑动窗口的大小}res[i - k + 1] = pq.peek()[0]; // 此时堆顶元素就是滑动窗口的最大值}return res;}}
- 时间复杂度:
,其中
n是数组nums的长度。在最坏情况下,数组nums中的元素单调递增,那么最终优先队列中包含了所有元素,没有元素被移除。由于将一个元素放入优先队列的时间复杂度为,因此总时间复杂度为
- 空间复杂度:
,即为优先队列需要使用的空间。这里所有的空间复杂度分析都不考虑返回的答案需要的
空间,只计算额外的空间使用
方法二:单调队列
我们可以顺着方法一的思路继续进行优化
由于我们需要求出的是滑动窗口的最大值,如果当前的滑动窗口中有两个下标 i 和 j,其中 i 在 j 的左侧(i < j),并且 i 对应的元素不大于 j 对应的元素(nums[i]≤nums[j]),那么会发生什么呢?
当滑动窗口向右移动时,只要 i 还在窗口中,那么 j 一定也还在窗口中,这是 i 在 j 的左侧所保证的。因此,由于 nums[j] 的存在,nums[i] 一定不会是滑动窗口中的最大值了,我们可以将 nums[i] 永久地移除
因此我们可以使用一个队列存储所有还没有被移除的下标。在队列中,这些下标按照从小到大的顺序被存储,并且它们在数组 nums 中对应的值是严格单调递减的。因为如果队列中有两个相邻的下标,它们对应的值相等或者递增,那么令前者为 i,后者为 j,就对应了上面所说的情况,即 nums[i] 会被移除,这就产生了矛盾
当滑动窗口向右移动时,我们需要把一个新的元素放入队列中。为了保持队列的性质,我们会不断地将新的元素与队尾的元素相比较,如果前者大于等于后者,那么队尾的元素就可以被永久地移除,我们将其弹出队列。我们需要不断地进行此项操作,直到队列为空或者新的元素小于队尾的元素
由于队列中下标对应的元素是严格单调递减的,因此此时队首下标对应的元素就是滑动窗口中的最大值。但与方法一中相同的是,此时的最大值可能在滑动窗口左边界的左侧,并且随着窗口向右移动,它永远不可能出现在滑动窗口中了。因此我们还需要不断从队首弹出元素,直到队首元素在窗口中为止
为了可以同时弹出队首和队尾的元素,我们需要使用双端队列。满足这种单调性的双端队列一般称作单调队列(单调队列是在队列中所有的元素都是单调的,要么单调增,要么单调减,新增元素时到队尾,此时队列不符合单调性就将队尾元素出队,直到队列单调或空)



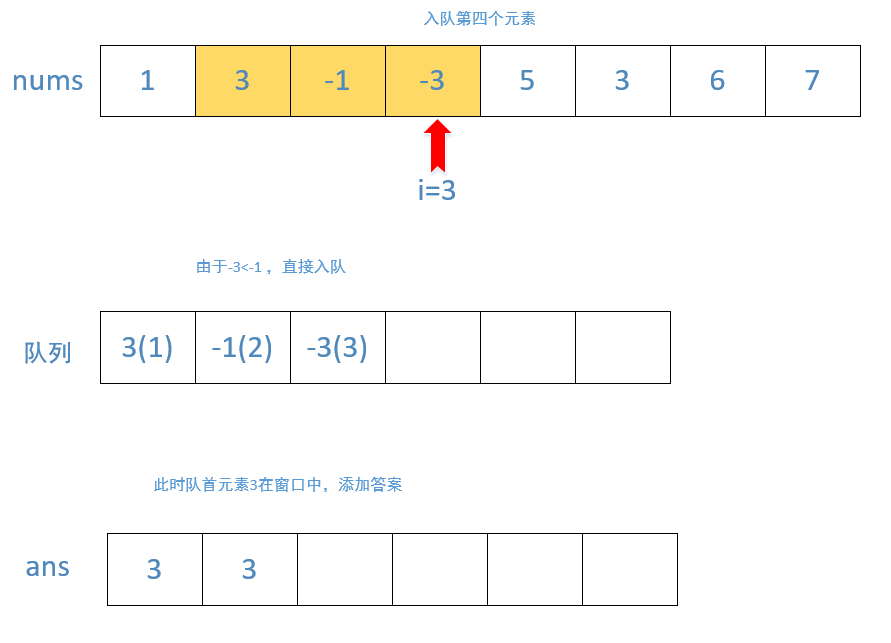
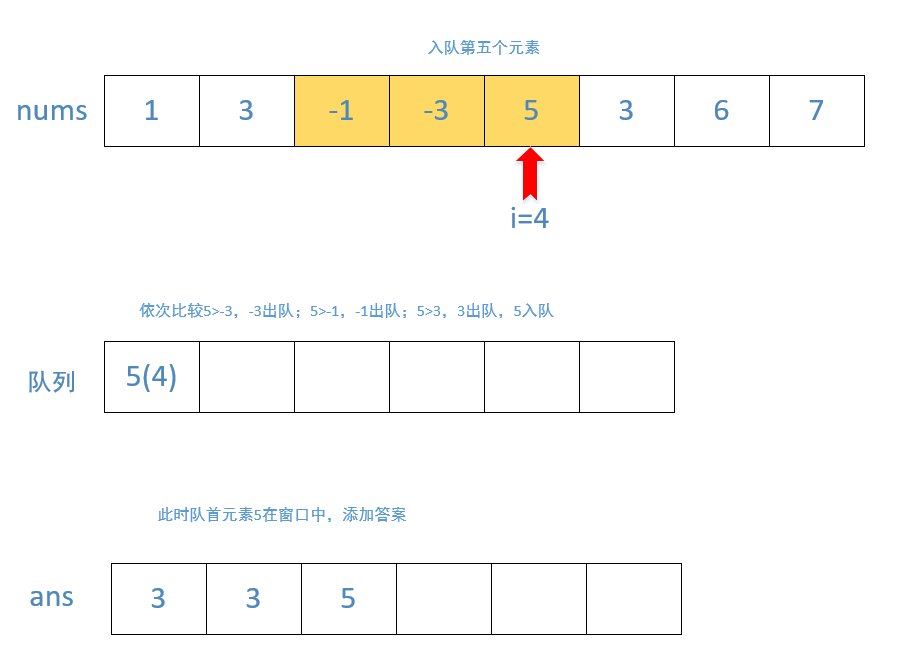



public int[] maxSlidingWindow(int[] nums, int k) {int n = nums.length;//创建双端队列Deque<Integer> deque = new ArrayDeque<>();//先初始化前K个元素for (int i = 0; i < k; i++) {//判断队列是否为空 或者当前入队元素是否大于队尾元素 大于则出队while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {deque.pollLast();}//当前元素入队//由于需要判断当前元素是否在窗口中,所以实际上队列中存储的为当前元素的下标//根据下标找元素比根据元素找下标方便deque.offerLast(i);}int[] ans = new int[n - k + 1];//添加当前最大元素ans[0] = nums[deque.peekFirst()];for (int i = k; i < n; i++) {//判断队列是否为空 或者当前入队元素是否大于队尾元素 大于则出队while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {deque.pollLast();}//当前元素入队deque.offerLast(i);//判断队首元素是否在窗口中while (deque.peekFirst() <= i - k) {deque.pollFirst();}//添加答案ans[i - k + 1] = nums[deque.peekFirst()];}return ans;}
- 时间复杂度:
,其中
n是数组nums的长度。每一个下标恰好被放入队列一次,并且最多被弹出队列一次 - 空间复杂度:
。与方法一不同的是,在方法二中我们使用的数据结构是双向的,因此「不断从队首弹出元素」保证了队列中最多不会有超过
k+1个元素
方法三:分块 + 预处理思路与算法
除了基于随着窗口的移动实时维护最大值的方法一以及方法二之外,我们还可以考虑其他有趣的做法
我们可以将数组 nums 从左到右按照 k 个一组进行分组,最后一组中元素的数量可能会不足 k 个。如果我们希望求出 nums[i] 到 nums[i+k−1] 的最大值,就会有两种情况:
- 如果
i是k的倍数,那么nums[i]到nums[i+k−1]恰好是一个分组。我们只要预处理出每个分组中的最大值,即可得到答案; - 如果
i不是k的倍数,那么nums[i]到nums[i+k−1]会跨越两个分组,占有第一个分组的后缀以及第二个分组的前缀。假设j是k的倍数,并且满足i < j ≤ i+k−1,那么nums[i]到nums[j−1]就是第一个分组的后缀,nums[j]到nums[i+k−1]就是第二个分组的前缀。如果我们能够预处理出每个分组中的前缀最大值以及后缀最大值,同样可以在的时间得到答案
因此我们用 prefixMax[i] 表示下标 i 对应的分组中,以 i 结尾的前缀最大值;suffixMax[i] 表示下标 i 对应的分组中,以 i 开始的后缀最大值。它们分别满足如下的递推式
以及
需要注意在递推 suffixMax[i] 时需要考虑到边界条件 suffixMax[n−1]=nums[n−1],而在递推 prefixMax[i] 时的边界条件 prefixMax[0]=nums[0] 恰好包含在递推式的第一种情况中,因此无需特殊考虑
在预处理完成之后,对于 nums[i] 到 nums[i+k−1] 的所有元素,如果 i 不是 k 的倍数,那么窗口中的最大值为 suffixMax[i] 与 prefixMax[i+k−1] 中的较大值;如果 i 是 k 的倍数,那么此时窗口恰好对应一整个分组,suffixMax[i] 和 prefixMax[i+k−1] 都等于分组中的最大值,因此无论窗口属于哪一种情况,
即为答案
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
int[] prefixMax = new int[n];
int[] suffixMax = new int[n];
for (int i = 0; i < n; ++i) {
if (i % k == 0) {
prefixMax[i] = nums[i];
}
else {
prefixMax[i] = Math.max(prefixMax[i - 1], nums[i]);
}
}
for (int i = n - 1; i >= 0; --i) {
if (i == n - 1 || (i + 1) % k == 0) {
suffixMax[i] = nums[i];
} else {
suffixMax[i] = Math.max(suffixMax[i + 1], nums[i]);
}
}
int[] ans = new int[n - k + 1];
for (int i = 0; i <= n - k; ++i) {
ans[i] = Math.max(suffixMax[i], prefixMax[i + k - 1]);
}
return ans;
}
}
- 时间复杂度:
,其中
n是数组nums的长度。我们需要的时间预处理出数组
prefixMax,suffixMax以及计算答案 - 空间复杂度:
,即为存储
prefixMax和suffixMax需要的空间

