leetcode-70：爬楼梯

问题

假设你正在爬楼梯。需要 n 阶你才能到达楼顶
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数

示例 1：
输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶

• 1 阶 + 1 阶
• 2 阶

示例 2：
输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶

• 1 阶 + 1 阶 + 1 阶
• 1 阶 + 2 阶
• 2 阶 + 1 阶

思路

爬到第一层楼梯有一种方法，爬到二层楼梯有两种方法

那么第一层楼梯再跨两步就到第三层 ，第二层楼梯再跨一步就到第三层

所以到第三层楼梯的状态可以由第二层楼梯和到第一层楼梯状态推导出来，那么就可以想到动态规划了

我们来分析一下，动规五部曲：

定义一个一维数组来记录不同楼层的状态

• 确定dp数组以及下标的含义
  • dp[i]：爬到第i层楼梯，有dp[i]种方法

• 确定递推公式
  • 如果可以推出dp[i]呢？
  • 从dp[i]的定义可以看出，dp[i] 可以有两个方向推出来
    • 首先是dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶就是dp[i]
    • 还有就是dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶不就是dp[i]
    • 那么dp[i]就是dp[i - ]与dp[i - 2]之和！
  • 所以dp[i] = dp[i - 1] + dp[i - 2]

在推导dp[i]的时候，一定要时刻想着dp[i]的定义，否则容易跑偏

这体现出确定dp数组以及下标的含义的重要性！

• dp数组如何初始化

  在回顾一下dp[i]的定义：爬到第i层楼梯，有dp[i]种方法

  那么i为0，dp[i]应该是多少呢，这个可以有很多解释，但都基本是直接奔着答案去解释的

  例如强行安慰自己爬到第0层，也有一种方法，什么都不做也就是一种方法即：dp[0] = 1，相当于直接站在楼顶

  但总有点牵强的成分

  那还这么理解呢：我就认为跑到第0层，方法就是0啊，一步只能走一个台阶或者两个台阶，然而楼层是0，直接站楼顶上了，就是不用方法，dp[0]就应该是0

  其实这么争论下去没有意义，大部分解释说dp[0]应该为1的理由其实是因为dp[0]=1的话在递推的过程中i从2开始遍历本题就能过，然后就往结果上靠去解释dp[0] = 1

  从dp数组定义的角度上来说，dp[0] = 0 也能说得通

  需要注意的是：题目中说了n是一个正整数，题目根本就没说n有为0的情况

所以本题其实就不应该讨论dp[0]的初始化！

所以我的原则是：不考虑dp[0]如何初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推，这样才符合dp[i]的定义

• 确定遍历顺序
  • 从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，遍历顺序一定是从前向后遍历的

• 举例推导dp数组
  • 举例当n为5的时候，dp table（dp数组）应该是这样的

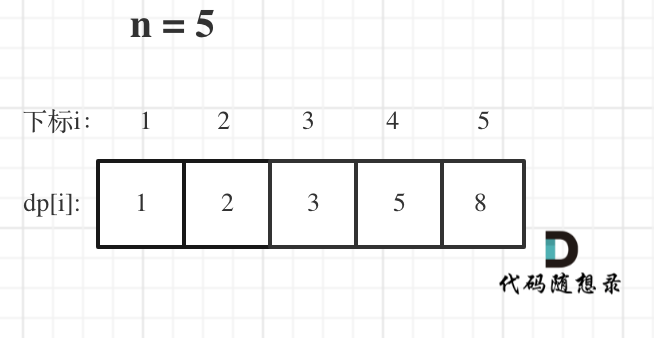
此时大家应该发现了，这不就是斐波那契数列么！

唯一的区别是，没有讨论dp[0]应该是什么，因为dp[0]在本题没有意义！

class Solution {
    public int climbStairs(int n) {
        if (n <= 1) 
            return n; 
        int[] dp = new int[n + 2];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) { // 注意i是从3开始的
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

• 时间复杂度：
• 空间复杂度：

优化一下空间复杂度，代码如下：

class Solution {
    public int climbStairs(int n) {
        if (n <= 1) 
            return n;
        int[] dp = new int[3];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            int sum = dp[1] + dp[2];
            dp[1] = dp[2];
            dp[2] = sum;
        }
        return dp[2];
    }
}

• 时间复杂度：
• 空间复杂度：