leetcode-235：二叉搜索树的最近公共祖先

问题

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]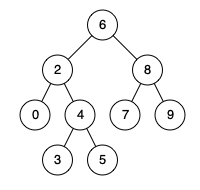

示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6

示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身

说明:

• 所有节点的值都是唯一的
• p、q 为不同节点且均存在于给定的二叉搜索树中

思路

在有序树里，如果判断一个节点的左子树里有p，右子树里有q呢？
其实只要从上到下遍历的时候，cur节点是数值在[p, q]区间中则说明该节点cur就是最近公共祖先了

普通二叉树求最近公共祖先需要使用回溯，从底向上来查找，二叉搜索树就不用了，因为搜索树有序（相当于自带方向），那么只要从上向下遍历就可以了

那么我们可以采用前序遍历（其实这里没有中节点的处理逻辑，遍历顺序无所谓了）

如图所示：p为节点3，q为节点5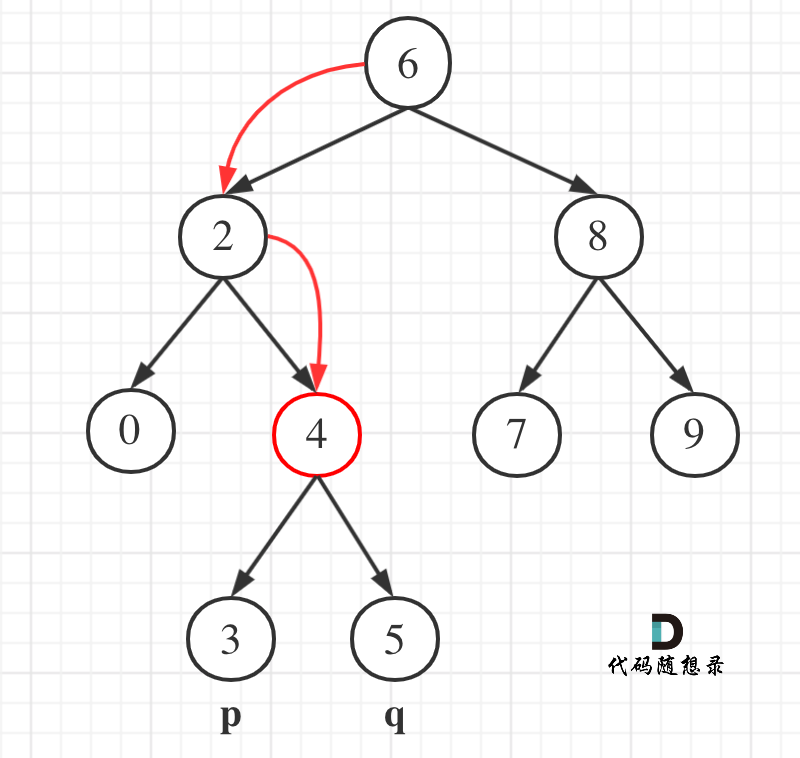

可以看出直接按照指定的方向，就可以找到节点4，为最近公共祖先，而且不需要遍历整棵树，找到结果直接返回

解法一：递归

递归三部曲如下：

• 确定递归函数返回值以及参数

  • 参数就是当前节点，以及两个结点 p、q
  • 返回值是要返回最近公共祖先，所以是TreeNode

    TreeNode traversal(TreeNode cur, TreeNode p, TreeNode q)

• 确定终止条件

  • 遇到空返回就可以了

    if (cur == null) return cur;

    其实都不需要这个终止条件，因为题目中说了p、q 为不同节点且均存在于给定的二叉搜索树中。也就是说一定会找到公共祖先的，所以并不存在遇到空的情况

• 确定单层递归的逻辑

  • 在遍历二叉搜索树的时候就是寻找区间[p.val, q.val]（注意这里是左闭右闭）
  • 那么如果 cur.val 大于 p.val，同时 cur.val 大于q.val，那么就应该向左遍历（说明目标区间在左子树上）
  • 需要注意的是此时不知道p和q谁大，所以两个都要判断

    if (cur.val > p.val && cur.val > q.val) {
    TreeNode left = traversal(cur.left, p, q);
    if (left != null) {
       return left;
    }
    }

    在这里调用递归函数的地方，把递归函数的返回值left，直接return

如果递归函数有返回值，如何区分要搜索一条边，还是搜索整个树

• 搜索一条边的写法： ```java if (递归函数(root.left)) return ;

if (递归函数(root.right)) return ;

- 搜索整个树写法：
```java
left = 递归函数(root.left);
right = 递归函数(root.right);
left与right的逻辑处理;

本题就是标准的搜索一条边的写法，遇到递归函数的返回值，如果不为空，立刻返回

• 如果 cur.val 小于 p.val，同时 cur.val 小于 q.val，那么就应该向右遍历（目标区间在右子树）

  if (cur.val < p.val && cur.val < q.val) {
  TreeNode right = traversal(cur.right, p, q);
  if (right != null) {
     return right;
  }
  }
  

• 剩下的情况，就是cur节点在区间(p.val <= cur.val && cur.val <= q.val)或者q.val <= cur.val && cur.val <= p.val)中，那么cur就是最近公共祖先了，直接返回cur

  class Solution {
  public TreeNode traversal(TreeNode cur, TreeNode p, TreeNode q) {
     if (cur == null) 
         return cur;
                                                     // 中
     if (cur.val > p.val && cur.val > q.val) {   // 左
         TreeNode left = traversal(cur.left, p, q);
         if (left != null) {
             return left;
         }
     }
  
     if (cur.val < p.val && cur.val < q.val) {   // 右
         TreeNode right = traversal(cur.right, p, q);
         if (right != null) {
             return right;
         }
     }
     return cur;
  } 
  
  public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
     return traversal(root, p, q);
  }
  }
  

  class Solution {
  public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
     if (root.val > p.val && root.val > q.val) {
         return lowestCommonAncestor(root.left, p, q);
     } else if (root.val < p.val && root.val < q.val) {
         return lowestCommonAncestor(root.right, p, q);
     } else return root;
  }
  }
  

解法二：迭代

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        while(root) {
            if (root.val > p.val && root.val > q.val) {
                root = root.left;
            } else if (root.val < p.val && root.val < q.val) {
                root = root.right;
            } else return root;
        }
        return null;
    }
}

解法三：官解，两次遍历

注意到题目中给出的是一棵「二叉搜索树」，因此我们可以快速地找出树中的某个节点以及从根节点到该节点的路径，例如我们需要找到节点 p：

• 从根节点开始遍历；
• 如果当前节点就是 p，那么成功地找到了节点；
• 如果当前节点的值大于 p 的值，说明 p 应该在当前节点的左子树，因此将当前节点移动到它的左子节点；
• 如果当前节点的值小于 p 的值，说明 p 应该在当前节点的右子树，因此将当前节点移动到它的右子节点。

对于节点 q 同理。在寻找节点的过程中，我们可以顺便记录经过的节点，这样就得到了从根节点到被寻找节点的路径

当我们分别得到了从根节点到 p 和 qq的路径之后，我们就可以很方便地找到它们的最近公共祖先了。显然，p 和 q 的最近公共祖先就是从根节点到它们路径上的「分岔点」，也就是最后一个相同的节点。因此，如果我们设从根节点到 p 的路径为数组 ，从根节点到 q 的路径为数组 ，那么只要找出最大的编号 i，其满足

那么对应的节点就是分岔点，即 p 和 q 的最近公共祖先就是 （或 ）

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        List<TreeNode> path_p = getPath(root, p);
        List<TreeNode> path_q = getPath(root, q);
        TreeNode ancestor = null;
        for (int i = 0; i < path_p.size() && i < path_q.size(); ++i) {
            if (path_p.get(i) == path_q.get(i)) {
                ancestor = path_p.get(i);
            } else {
                break;
            }
        }
        return ancestor;
    }

    public List<TreeNode> getPath(TreeNode root, TreeNode target) {
        List<TreeNode> path = new ArrayList<TreeNode>();
        TreeNode node = root;
        while (node != target) {
            path.add(node);
            if (target.val < node.val) {
                node = node.left;
            } else {
                node = node.right;
            }
        }
        path.add(node);
        return path;
    }
}