问题

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有从根节点到叶子节点路径总和等于给定目标和的路径
叶子节点 是指没有子节点的节点

示例 1：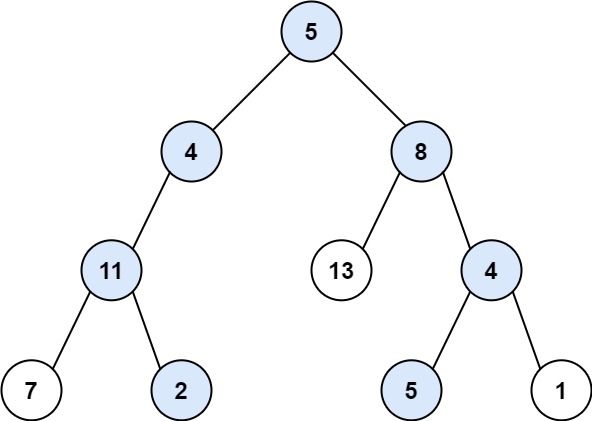
leetcode-113：路径总和Ⅱ - 图1

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：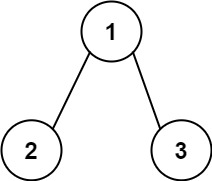
leetcode-113：路径总和Ⅱ - 图2
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：
输入：root = [1,2], targetSum = 0
输出：[]

解法一：递归

因为要遍历整个树，找到所有的路径，所以递归函数不需要返回值

  1. class Solution {
  2.     List<List<Integer>> res = new LinkedList<List<Integer>>();
  3.     Deque<Integer> path = new LinkedList<Integer>();
  5.     public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
  7.         dfs(root, targetSum);
  8.         return res;
  9.     }
  11.     public void dfs(TreeNode root, int targetSum){
  12.         //主要是用于判断叶子节点
  13.         if(root == null){ 
  14.             return ;
  15.         }
  16.         path.offerLast(root.val);
  17.         targetSum -= root.val;
  18.         if(root.left == null && root.right == null && targetSum == 0){
  19.             res.add(new LinkedList<Integer>(path));
  20.         }
  21.         dfs(root.left, targetSum);
  22.         dfs(root.right, targetSum);
  23.         path.pollLast();
  24.     }
  25. }
  • 时间复杂度：leetcode-113：路径总和Ⅱ - 图3，其中 N 是树的节点数。在最坏情况下，树的上半部分为链状，下半部分为完全二叉树，并且从根节点到每一个叶子节点的路径都符合题目要求。此时，路径的数目为 leetcode-113：路径总和Ⅱ - 图4，并且每一条路径的节点个数也为 leetcode-113：路径总和Ⅱ - 图5，因此要将这些路径全部添加进答案中
  • 空间复杂度：leetcode-113：路径总和Ⅱ - 图6，其中 N 是树的节点数。空间复杂度主要取决于栈空间的开销，栈中的元素个数不会超过树的节点数

解法二：广度优先搜索

当我们遍历到叶子节点，且此时路径和恰为目标和时，我们就找到了一条满足条件的路径
为了节省空间，我们使用哈希表记录树中的每一个节点的父节点。每次找到一个满足条件的节点，我们就从该节点出发不断向父节点迭代，即可还原出从根节点到当前节点的路径

  1. class Solution {
  2.     List<List<Integer>> ret = new LinkedList<List<Integer>>();
  3.     Map<TreeNode, TreeNode> map = new HashMap<TreeNode, TreeNode>();
  5.     public List<List<Integer>> pathSum(TreeNode root, int sum) {
  6.         if (root == null) {
  7.             return ret;
  8.         }
  10.         Queue<TreeNode> queueNode = new LinkedList<TreeNode>();
  11.         Queue<Integer> queueSum = new LinkedList<Integer>();
  12.         queueNode.offer(root);
  13.         queueSum.offer(0);
  15.         while (!queueNode.isEmpty()) {
  16.             TreeNode node = queueNode.poll();
  17.             int rec = queueSum.poll() + node.val;
  19.             if (node.left == null && node.right == null) {
  20.                 if (rec == sum) {
  21.                     getPath(node);
  22.                 }
  23.             } else {
  24.                 if (node.left != null) {
  25.                     map.put(node.left, node);
  26.                     queueNode.offer(node.left);
  27.                     queueSum.offer(rec);
  28.                 }
  29.                 if (node.right != null) {
  30.                     map.put(node.right, node);
  31.                     queueNode.offer(node.right);
  32.                     queueSum.offer(rec);
  33.                 }
  34.             }
  35.         }
  37.         return ret;
  38.     }
  40.     public void getPath(TreeNode node) {
  41.         List<Integer> temp = new LinkedList<Integer>();
  42.         while (node != null) {
  43.             temp.add(node.val);
  44.             node = map.get(node);
  45.         }
  46.         Collections.reverse(temp);
  47.         ret.add(new LinkedList<Integer>(temp));
  48.     }
  49. }