问题

有一堆石头，用整数数组stones表示。其中 stones[i] 表示第 i 块石头的重量
每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

  • 如果 x == y，那么两块石头都会被完全粉碎；
  • 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x

最后，最多只会剩下一块 石头。返回此石头最小的可能重量 。如果没有石头剩下，就返回 0

示例 1：
输入：stones = [2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值

示例 2：
输入：stones = [31,26,33,21,40]
输出：5

示例 3：
输入：stones = [1,2]
输出：1

动态规划

本题其实就是尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，这样就化解成01背包问题了

本题物品的重量为store[i]，物品的价值也为store[i]，对应着01背包里的物品重量weight[i]和物品价值value[i]

接下来进行动规五步曲：

  • 确定dp数组以及下标的含义

    • dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背dp[j]这么重的石头

  • 确定递推公式

    • 01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
    • 本题则是：**dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);**

  • dp数组如何初始化

    • 既然dp[j]中的j表示容量，那么最大容量（重量）是多少呢，就是所有石头的重量和
    • 因为提示中给出1 <= stones.length <= 30，1 <= stones[i] <= 1000，所以最大重量就是30 * 1000
    • 而我们要求的target其实只是最大重量的一半，所以dp数组开到15000大小就可以了
    • 接下来就是如何初始化dp[j]呢，因为重量都不会是负数，所以dp[j]都初始化为0就可以了，这样在递归公式dp[j] = max(dp[j], dp[j - stones[i]] + stones[i])中dp[j]才不会初始值所覆盖
      1. int[] dp = new int[15001];

  • 确定遍历顺序

    • 如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒叙遍历！
      1. for (int i = 0; i < stones.length; i++) { // 遍历物品
      2. for (int j = target; j >= stones[i]; j--) { // 遍历背包
      3.    dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
      4. }
      5. }

  • 举例推导dp数组

    • 举例，输入：[2,4,1,1]，此时target = (2 + 4 + 1 + 1)/2 = 4 ，dp数组状态图如下：

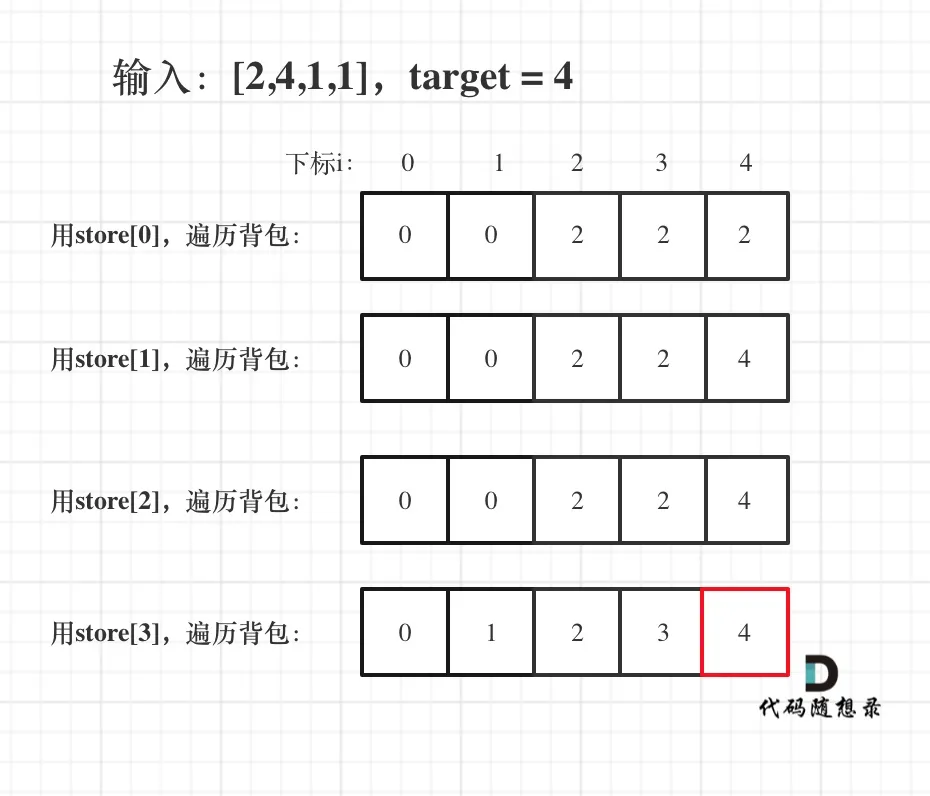
640.webp
最后dp[target]里是容量为target的背包所能背的最大重量
那么分成两堆石头，一堆石头的总重量是dp[target]，另一堆就是sum - dp[target]
在计算target的时候，target = sum / 2 因为是向下取整，所以**sum - dp[target]**一定是大于等于**dp[target]**的
那么相撞之后剩下的最小石头重量就是(sum - dp[target]) - dp[target]

  1. class Solution {
  2.     public int lastStoneWeightII(int[] stones) {
  3.         int[] dp = new int[15001];
  4.         int sum = 0;
  5.         for (int i = 0; i < stones.length; i++) 
  6.             sum += stones[i];
  7.         int target = sum / 2;
  9.         for (int i = 0; i < stones.length; i++) { // 遍历物品
  10.             for (int j = target; j >= stones[i]; j--) { // 遍历背包
  11.                 dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
  12.             }
  13.         }
  14.         return sum - dp[target] - dp[target];
  15.     }
  16. }
  • 时间复杂度：leetcode-1049：最后一块石头得重量Ⅱ - 图2，m是石头总重量（准确的说是总重量的一半），n为石头块数
  • 空间复杂度：leetcode-1049：最后一块石头得重量Ⅱ - 图3